• 다음 내용은 [CS-188] Introduction to Aritificial Intelligence, UC Berkeley, Fall 2018의 Readings-Note5을 정리하였음을 밝힙니다.
• 스스로 이해하기에 영문 용어가 이해하기 직관적이면 그대로 사용했습니다.

Summary

강화학습은 사전에 트랜지션 함수 $T$와 보상 함수 $R$을 알지 못한 상태에서 MDP 문제를 최적의 정책 $\pi^*$를 해결한다. 강화학습을 통해 에이전트는 학습 도중 시도와 에러를 거치면서 최적의 정책을 찾아간다. 이때 강화학습의 방법론에는 다음과 같은 것들이 존재한다.

• Model-based learning: 모델 기반 학습은 트랜지션 함수 $T$와 보상 함수 $R$이 주어질 때 MDP를 VI, PI 등을 통해 푼다.

• Model-free learning: $T$와 $R$이 없을 때 사용하는 학습 방법이다.
  (1). Direct evaluation: 직접 정책 $\pi$에 수렴한다.
  (2). Temporal difference learning: 위와 비슷하게 정책을 따라 수렴할 때까지 보상을 계산하는데, 샘플 값의 평균을 취한다.
  (3). Q-Learning: q-값 반복 업데이트를 통해 직접적으로 $\pi^*$를 학습한다. 최적은 아니지만 부분적으로 최적인 행동을 통해 최적 정책을 학습하는 방법이다.
  (4). Approximate Q-Learning: 학습을 일반화하는 상태 별 feature 기반 표현 방법을 사용한다.

Reinforcement Learning

MDP는 VI, PI 등 각 상태를 계산해 최적의 값과 최적의 정책을 사전에 계산해 풀 수 있는 오프라인 문제(offline planning) 중 하나다. 즉 에이전트는 트랜지션 함수와 보상 함수를 사전에 모두 제공받으며 MDP로 인코딩된 공간을 탐색하기에 충분한 사전 정보를 사전에 계산할 수 있다.

반면 온라인 탐색 문제(online planning)는 이와 다르다. 에이전트는 직접 탐험(exploration)하면서 트랜지션 함수와 보상 함수가 무엇인지 배워가야 한다. 시도와 실패(trial and error)를 통해 에이전트는 점차 어떤 선택이 더 큰 보상으로 이어지는지 깨닫게 된다.

피드백 시간이 늘어남에 따라 에이전트는 점차 최적의 정책에 가까운 정책을 만들어 낼 것이다. 학습을 통해 에이전트가 사전에 알지 못하던 정보를 파악해 최적의 해결책을 찾을 수 있다는 것이 강화 학습(reinforcement learning)의 요지다.

• 샘플(sample) $(s, a, s', r)$: 현재 에이전트가 있는 $s$에서 행동 $a$를 할 때 이어지는 다음 상태 $s'$와 그때 받는 보상 $r$

• 에피소드(episode): 샘플의 집합

• 강화학습의 종류: (1). 모델 기반 학습: 샘플과 함께 트랜지션 및 보상 함수를 사용한다. (2). 모델 프리 학습: MDP의 트랜지션 및 보상 함수를 통해 모델링하지 않고 상태별 값과 q-값을 직접 계산하는 학습 방법이다.

Model-Based Learning

모델 기반 학습에서 에이전트는 트랜지션 함수를 추정한 $\hat{T}(s,a,s')$를 q-상태 $(s,a)$를 겪고 다음 상태 $s'$를 얻는 횟수를 카운트해 사용한다. 즉 $s$ 상태에서 $a$를 통해 $s'$가 나오는 확률이 어떤지 경험적으로 확률로 만드는 것이다.

이때 트랜지션 추정 함수 $\hat{T}$는 샘플 $(s,a,s')$ 개수를 q-상태 $(s,a)$를 경험한 모든 인스턴스의 수로 나눈 정규화가 필요하다. 이 정규화를 통해 이 q-상태에서 특정 $s'$가 나오는 확률을 추정할 수 있다.

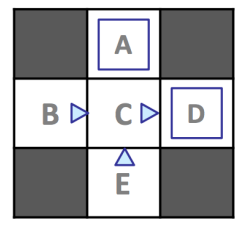
위 MDP를 탐험하면서 에이전트가 모은 에피소드는 다음과 같다.

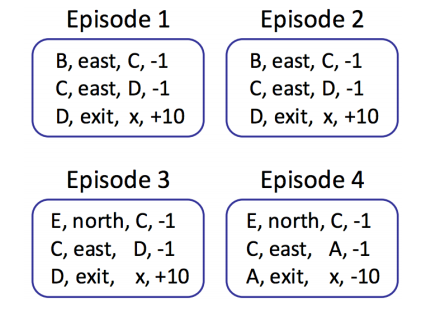
총 12개의 샘플에 해당하는 상태 $s$와 행동 $a$, 이에 따라 각 $s'$이 나올 확률을 구해보자.

$s$	$a$	$s'$	$count$	$\hat{T}(s,a,s')$	$\hat{R}(s,a,s')$
$A$	exit	$x$	1	1	-10
$B$	east	$C$	2	1	-1
$C$	east	$A$	1	0.25	-1
$C$	east	$D$	3	0.75	-1
$D$	east	$X$	3	1	+10
$E$	north	$C$	2	1	-1

샘플링이 더 많을 수록 트랜지션 추정 함수와 보상 추정 함수는 기존의 함수에 더 가까워질 것이다. 즉 탐색을 하면서 에이전트는 모델을 효율적으로 학습할 수 있다.

Model-Free Learning

에이전트가 $\hat{T}, \hat{S}$를 추정해 기존의 MDP처럼 접근하는 모델 기반 학습과 달리 모델 프리 학습은 $V, Q$에 직접적으로 접근한다. 이 샘플에서 나타나는 상태 값 또는 q-상태 값이 본질적으로는 올바른 빈도로 나타날 것이기 때문에 모델 기반 학습과 같이 사용할 수 있다.

모델을 사용하지 않은 모델 프리 학습에는 두 가지 종류가 있다.

수동적 강화학습(passive reinforcement learning)에서 에이전트는 정책을 받고 이에 따라 경험하는 에피소드를 통해 상태 값을 학습한다.

반면 능동적 강화학습(active reinforcement learning)에서 에이전트는 학습하며 얻은 피드백을 통해 자신의 정책을 반복적으로 업데이트해나간다. 충분한 탐색이 있다면 이때 에이전트는 최적의 정책에 수렴하는 정책을 만들어낼 수 있다.

먼저 상태 값 $V$를 직접 알아내는 direct evaluation과 temporary difference learning을 알아보자.

Direct Evaluation

정책 $\pi$를 고정시킨 뒤에 에이전트가 이 정책을 따른 에피소드를 모으는 방법이다. 이때 에이전트는 방문한 횟수 및 상태에서 얻은 총 유틸리티(utility) 카운트를 유지한다. 상태 $s$의 추정 값은 곧 $s$를 방문한 수로 $s$에서 얻은 총 유틸리티를 나눈 값이다.

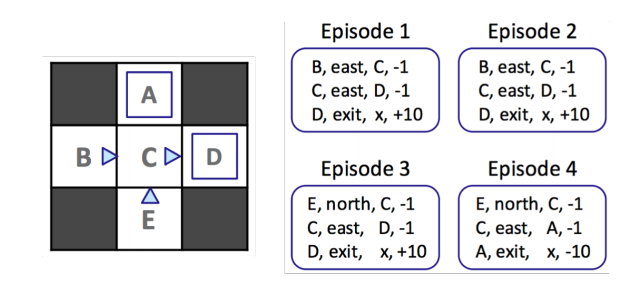
모델 기반 학습에서 사용한 예제다. 트랜지션, 보상 함수는 고려하지 말고 각 상태에서 얻어낼 수 있는 값만 위주로 살펴보자.

$s$	Total Reward	Times Visited	$V^{\pi}(s)$
$A$	-10	1	-10
$B$	16	2	8
$C$	16	4	4
$D$	30	3	10
$E$	-4	2	-2

하지만 이 방법은 상태 간 트랜지션에 관한 정보를 사용하지 않기 때문에 수렴할 때까지 시간이 다소 많이 필요하다. temporal difference learning을 통해 수렴할 때까지 시간이 필요한 이 간단한 (brute) 알고리즘보다 나은 대안을 찾아보자.

Temporal Difference Learning

모든 경험에서 학습하자라는 아이디어를 사용하는 TD 학습은 벨만 방정식에서 사용한 successor 상태의 discounted 값 weighted 평균을 가중치(weight) 없이 구한다.

• 벨만 방정식: $V^{\pi}(s)=\sum\limits_{s'}T(s,\pi(s),s')[R(s,\pi(s),s')+\gamma V^{\pi}(s')]$

• exponential moving average: 모든 상태 $s$에서 $V^{\pi}(s)$는 0으로 초기화된다. 각 타임 스탬프마다 에이전트가 상태 $s$에서 $a$로 $s'$로 이동하고, 보상 $R(s,\pi(s),s')$를 받는다. $\gamma$를 적용한 이후 상태 $s'$의 보상 합계를 통해 샘플 값(sample value)을 얻을 수 있다.

• sample: $R(s,\pi(s),s')+\gamma V^{\pi}(s')$

이 샘플을 정책 $\pi$를 사용해 얻어낼 상태 $s$의 값 $V$로 사용하자. 타임 스탬프마다 얻을 수 있는 이 상태 값 $V^{\pi}(s)$과 샘플을 함께 사용해 다음 상태 값을 업데이트하자.

• update rule: $V^{\pi}(s) \leftarrow (1-\alpha)V^{\pi}(s)+\alpha*sample$

$\alpha$는 지금까지 얻은 샘플을, 나머지는 상태 값 $V^{\pi}(s)$가 이후 상태 값에 반영되는 비중을 뜻하는 학습률(learning rate)다. $\alpha$가 높다면 여태까지 모은 샘플들에 더 많은 비중을 준다는 뜻이다. 일반적으로 처음 시작할 때에는 $\alpha=1$로 설정해 처음 주어지는 어떤 종류의 샘플이라도 전적으로 사용하며, 점차 모델 $V^{\pi}(s)$에 영향을 미치지 않을 0으로 수렴해간다.

그렇다면 이 샘플을 사용한 모델 업데이트는 언제 멈춰야 할까? $k$번 업데이트한다고 가정한다면 위 업데이트 규칙은 이렇게 표현할 수 있다.

• k-th update rule: $V^{\pi}_k(s) \leftarrow (1-\alpha)V^{\pi}_{k-1}(s)+\alpha*sample_k$

재귀적으로 모델 $V_k^{\pi}(s)$는 계속해서 업데이트되는데, 최근에 더해지는 샘플에 더 많은 가중치가 부여된다. 자연스럽게 더해지는 샘플에 적용되는 학습률 $1-\alpha$는 0에 수렴해, 업데이트 역시 종료에 가까워진다.

TD 학습을 정리하자면 다음과 같은 특징이 있다.

• 모든 타임 스탬프에서 학습하기 때문에 상태 트랜지션에서 에이전트가 얻는 정보를 수렴할 때까지 연산에 활용할 수 있다.

• 오래된(부정확할 확률이 높은) 샘플에는 가중치가 적다.

• DE보다 더 적은 수의 에피소드만으로 훨씬 빠른 속도로 실제 상태 값을 학습할 수 있다.