• 다음 내용은 [CS-188] Introduction to Aritificial Intelligence, UC Berkeley, Fall 2018의 Readings-Note4을 정리하였음을 밝힙니다.
• 스스로 이해하기에 영문 용어가 이해하기 직관적이면 그대로 사용했습니다.

MDPs

4. The Bellman Equation

벨만 방정식을 통해 MDP를 수학적으로 풀 수 있다. 이때 agent가 얻을 수 있는 utility의 최적화된 값에 대한 두 가지 정의가 있다.

• $V^*(s)$: agent가 상태 $s$에서 시작, optimal하게 행동한다면 행동 가능한 타임 스탬프 동안 얻을 수 있는 utility 기댓값

• $Q^*(s,a)$: agent가 상태 $s$에서 시작, 행동 $a$를 시작한 뒤 optimal하게 행동한다면 이후 얻을 수 있는 utility 기댓값

이때 $V^*(s)$를 앞서 정의한 MDP 개념으로 표현할 수 있다.

• $V^*(s)=max_{a}\sum_{s'}T(s,a,s')[R(s,a,s')+\gamma V^*(s')]$

q-state 또한 MDP를 통해 표현해보자.

• $Q^*(s,a)=\sum_{s'}T(s,a,s')[R(s,a,s')+\gamma V^*(s')]$

이때 $T(s,a,s')[R(s,a,s')+\gamma V^*(s')]$는 상태 $s$에서 행동 $a$를 통해 다음 상태 $s'$에 도달한 뒤 optimal하게 행동했을 때 얻을 수 있는 모든 utility의 총합이다. $\gamma$를 통해 $s'$ 이후부터 얻을 utility를 $s$의 시점에서는 가중치를 적게 준 채로 보고 있다는 데 주의하자.

따라서 $\sum_{s'}T(s,a,s')[R(s,a,s')+\gamma V^*(s')]$는 $Q(s,a)$를 택한 이후 optimal하게 얻을 수 있는 utility 기댓값임을 알 수 있다. 자연스럽게, 이 중 가장 최댓값을 택하는 길을 고르자.

• $V^*(s)=max_a Q^*(s,a)$

벨만 방정식은 지금 상태 $s$에서 이후 모든 상태 $s'$로 이어지는 값 중 최댓값을 고르는 식을 1). 어떤 행동 $a$가 있는지 확인한다. 2). 행동 별로 얻을 수 있는 값을 본다. 3). 최댓값을 얻는다. 이와 같은 방법으로 나눈다는 점에서 다이나믹 프로그래밍 dp이다.

또한 벨만 방정식이 각 상태에서 성립한다면 각 상태 $s$에서 얻을 수 있는 상태 $s$의 $V^(s)$는 우리가 얻고 싶은 최적화된 값과 같다.

• $\forall s \in S,\;V(s)=V^*(s)$

5. Value Iteration

$V_k(s)$는 $k$번 행동할 수 있는 때 상태 $s$에서 시작해서 얻을 수 있는 최적화된 utility 값이라고 하자. 타임 스탬프 $k$를 통해 utility를 확인한다는 점에서 마르코프 결정 과정은 주어진 $k$ 번만에 종료한다.

이 타임 스탬프를 사용해서 타임 스탬프가 추가되더라도(즉 한 번 더 행동해 보상을 받는다 할지라도) 값이 바뀌지 않고, 특정한 값으로 수렴하는 식을 표현해 보자.

• $\forall s \in S, \; V_0(s)=0$

• $\forall s \in S, V_{k+1}(s) \leftarrow max_a\sum_{s'}T(s,a,s')[R(s,a,s')+\gamma V_k(s')]$

아무런 행동도 하지 않은 상태에서는 얻은 보상이 없고, 다음 타임 스탬프 $k+1$을 살펴볼 때에는 $Q^*(s,a)$를 최대화하는 값을 택해야 한다.

이전의 값을 그대로 재사용한다. 벨만 방정식을 사용할 때와 같이, VI 역시 dp라는 점을 알 수 있다. 하지만 VI는 수렴할 때까지, 벨만 방정식은 optimality가 이루어졌다는 점을 알려준다는 점에서 다르다. 수렴한 뒤에 벨만 방정식이 모든 상태 $s$에서 성립할 것이다.

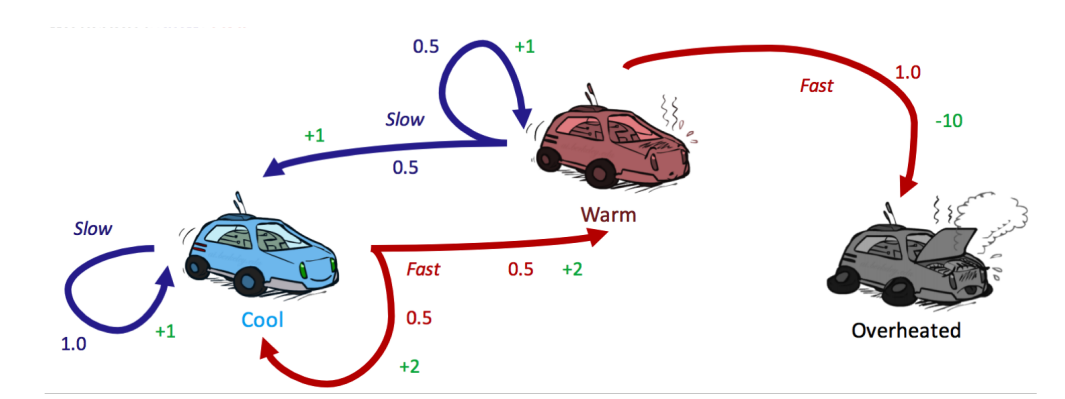
위 그래프를 통해 VI를 시작해보자.

1. 모든 상태에서 아무런 보상이 주어지지 않았다.

	cool	warm	overheated
$V_0$	0	0	0

2. 타임 스탬프 1에서 얻을 수 있는 $V$를 업데이트하자.

$V_1(cool)=max(1*1, 0.5*2+0.5*2)=max(1,2)=2$
$V_1(warm)=max(0.5*1+0.5*1, 1*(-10))=max(1,-10)=-10$
$V_1(overheated)=max()=0$

	cool	warm	overheated
$V_0$	0	0	0
$V_1$	2	1	0

• overheated된 상태에서는 행동 $a$가 주어지지 않는다.

3. 타임 스탬프 2에서 얻을 수 있는 $V$를 업데이트하자.
   $V_2(cool)=max(1*(1+0.5*2), 0.5*(2+0.5*2)+0.5*(2+0.5*1))=max(2,2.75)=2.75$
   $V_2(warm)=max(0.5*(1+0.5*2)+0.5*(1+0.5*1), 1*(-10+0.5*0))=max(1.75,-10)=1.75$
   $V_2(overheated)=max()=0$

	cool	warm	overheated
$V_0$	0	0	0
$V_1$	2	1	0
$V_2$	2.75	1.75	0

종료 상태에 대한 $V^*(s)$는 언제나 0으로 고정되기 때문에 어떤 행동 $a$도 일어나지 않는다.

6. Policy Extraction

MDP의 가장 큰 목적 MDPs를 푸는 최적화된 정책 $\pi^*$를 구하는 것이다. 정책 추출 policy extraction을 통해 얻어낸 정책 $\pi$가 과연 모든 상태에서 optimal한 값을 얻을 수 있는 방법일지 확인해보자. 즉 상태 $s$에서 해야 하는 행동 $a$는 utility 기댓값 중 최댓값을 가져와야 한다. 이를 앞서 표현한 식을 사용해 다시 풀어 쓰자.

• $\forall s \in S, \; \pi^*(s)=argmax_a Q^*(s,a)=argmax_a \sum_{s'}T(s,a,s')[R(s,a,s')+\gamma V^*(s')]$

$argmax$ 연산이 그 상태에서 optimal a를 얻는 데 필요한 유일한 연산이다.

7. Policy Iteration

VI는 반복할 때마다 모든 상태 $s$의 값을 업데이트해야 하기 때문에 시간적으로 비효율적이다. 각 행위 $a$에 대한 q-value를 구하려면 모든 $a$에 대한 반복이 필요하기 때문에 $O(|S|^2|A|)$이다. 정책 반복 policy iteration을 통해 VI의 최적화는유지하면서 성능을 올릴 수 있다.

1.초기 정책을 정의하자. PI는이 초기 정책이 $\pi^*$에 근접하게 설정될 수록 더 빠른 속도로 수렴한다.

2. 정책 평가 policy evaluation를 통해 현재 정책의 utility 기댓값을 확인하자.

• $V^{\pi}(s)=\sum_{s'}T(s,\pi(s),s')[R(s,\pi(s),s')+\gamma V^{\pi}(s')]$

$i$ 단계의 정책을 $\pi^i$라고 할 때, 각 상태 $s$에서 하는 행위 $a$를 고정하기 때문에 최댓값을 구하지 않아도 된다.

3. 정책 성능 향상 policy improvement 과정을 사용해 더 나은 정책을 만들자. 정책 평가로 만들어낸 $V^{\pi}(s)$에 PE를 사용하자.

• $\pi_{i+1}(s)=argmax_a \sum_{s'}T(s,a,s')[R(s,a,s')+ \gamma V^{\pi_i}(s')]$

정책 $\pi$가 수렴할 때까지 PE, PI를 반복하자. 수렴 조건은 $\pi_{i+1}==\pi_{i}$이다.

이 PI를 VI에서 사용한 자동차 그래프에서 다시 사용해보자. VI에서 각 상태 별로 값을 업데이트한 바와 달리 값을 구하는 속도가 빨라진다.

1. 초기 정책은 slow로 설정하자.

	cool	warm	overheated
$\pi_0$	slow	slow

2. 종료 상태라면 값은 0으로, 그렇지 않다면 초기 정책을 사용해 값을 계산하자.

$V^{\pi_0}(cool)=1*(1+0.5*V^{\pi_0}(cool))$
$V^{\pi_0}(cool)=2$

$V^{\pi_0}(warm)=0.5*(1+0.5*V^{\pi_0}(cool))+0.5*(1+0.5*V^{\pi_0}(warm))$
$V^{\pi_0}(warm)=2$

	cool	warm	overheated
$\pi_0$	slow	slow
$V^{\pi_0}$	2	2	0

3. 정책 추출 PE를 통해 새로운 정책을 만들어내자.

$\pi_1(cool)=argmax(slow:1*(1+0.5*2), fast:0.5*(2+0.5*2)+0.5*(2+0.5*2))=argmax(slow:2,fast:3)=fast$
$\pi_1(warm)=argmax(slow:0.5*(1+0.5*2)+0.5*(1+0.5*2), fast:1*(-10+0.5*0))=argmax(slow:3,fast:-10)=slow$

	cool	warm	overheated
$\pi_0$	slow	slow
$\pi_1$	fast	slow

4. 다음 단계의 정책과 현재 정책이 같을 때까지, 즉 수렴할 때까지 이 과정을 반복하자.

	cool	warm	overheated
$\pi_0$	slow	slow
$\pi_1$	fast	slow
$\pi_2$	fast	slow

따라서 $\pi^*=\pi^1$

Summary

• Value Iteration: 수렴할 때까지 업데이트를 반복해 상태 별 최적 값을 계산한다.

• Policy Evaluation: 특정 정책을 사용했을 때 상태의 값을 계산한다.

• Policy Extraction: 해당 상태 별 값을 통해 정책을 만들어낸다. 상태가 최적화된 상태라면 추출된 정책 또한 최적화된다.

• Policy Iteration: 정책 평가 및 정책 추출을 한데 묶어 최적화된 정책에 수렴할 때까지 반복하는 기법이다. VI보다 일반적으로 성능이 뛰어난데, 상태 값보다 정책이 더 빨리 수렴할 확률이 높기 때문이다.