• 다음 내용은 [CS-188] Introduction to Aritificial Intelligence, UC Berkeley, Fall 2018의 Readings-Note6을 정리하였음을 밝힙니다.
• 스스로 이해하기에 영문 용어가 이해하기 직관적이면 그대로 사용했습니다.

Probabilistic Inference

비결정적(nondeterministic) 사건 간의 관계를 모델링할 때 확률적 추론(probabilistic inference)을 사용할 수 있다.

계절과 온도, 날씨로 주어진 상태(state) 별 확률을 통해 확률적 추론을 확인해보자. 다음과 같이 각 테이블의 확률이 각 가능한 결과(outcome)가 일어날 가능성(likelihood)를 나타낸 것을 결합 확률 분포(joint distribution)라고 한다.

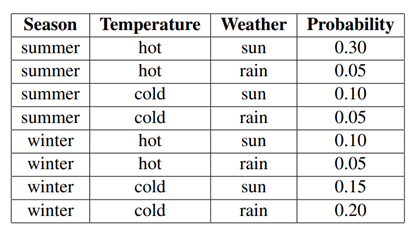
위 테이블을 사용해 날씨가 맑을 확률, 겨울일 때 날씨의 확률 분포, 비가 오고 추울 때 겨울일 확률, 온도가 추울 때 날씨와 계절 확률 분포 등을 계산할 수 있다.

주어진 조건에 따라 하나씩 확률을 카운트해 우리가 원하는 확률을 얻어낼 수 있다.

가령 날씨가 맑을 확률은 $P(W=sum)$으로 다른 조건(계절, 온도)과 관계없이 날씨만 보고 확률을 구하면 된다. 즉 $0.30+0.10+0.10+0.15=0.65$를 바로 구할 수 있다.

주어진 조건을 하나씩 헤아리는 열거식 추론(inference by enumeration)에 다음과 같은 변수 타입을 고려할 수 있다.

• 쿼리 변수 $Q_i$: 아직 알지 못하는, 구하고자 하는 변수

• 에비던스(evidence) 변수 $e_i$: 이미 알고 있는 관측된 변수

• 히든(hidden) 변수: 현재 계산하려고 하는 분포에는 없지만 전체 결합 분포 상에는 존재하는 확률 변수

에비던스 변수와 연결된(consistent) 모든 행을 모아 히든 변수 합계를 내리자. 마지막으로 정규화를 통해 확률 분포를 구하자.

가령 $P(W|S=winter)$는 계절이 겨울일 때 날씨 확률을 구해보자.

먼저 각 날씨 별로 계절이 겨울인 확률을 주어진 결합 분포에서 골라 합하자(unnormalized sum). 이후 각 확률(0.25, 0.25)을 총 합(0.5)로 나눠 정규화한다. 따라서 겨울일 때 맑을 확률, 겨울일 때 비가 올 확률을 구할 수 있다.

결합 확률 분포가 주어질 때 이러한 열거식 확률 추론은 간단한 구할 수 있다.

Bayes Nets (Representation)

결합 분포를 사용한 쿼리 변수 표현은 원하는 쿼리 변수 하나를 표현하기에는 간단하지만 전체 결합 분포 테이블을 채우기에는 너무 많은 시간이 걸린다. 변수 $n$개가 각각 도메인 $d$를 가질 때 결합 분포 테이블 크기는 $d^n$이기 때문이다.

베이즈 넷(Bayes Nets)은 조건부 확률을 통해 이 엄청난 크기의 메모리 낭비를 줄일 수 있다. 모든 확률 정보가 아니라 사이클이 없는 방향 그래프(directed acyclic graph, DAG)로 조그마한 로컬 확률을 여러 개 표시하자. 이 그물처럼 생긴 그래프를 통해 변수 간의 관계를 간단히 계산할 수 있다.

그래프의 각 노드는 하나의 단일한 랜덤 변수를 의미하고, 연결된 간선은 조건부 확률을 의미한다. 즉 노드 $A$에서 노드 $B$로 이어진 간선은 $P(B|A)$를 뜻한다. 따라서 변수 $X$에 대한 노드가 있다면 $A_1, A_2, ..., A_N$에서 연결된 $X$는 곧 $P(X|A_1,A_2,...,A_N)$이다.

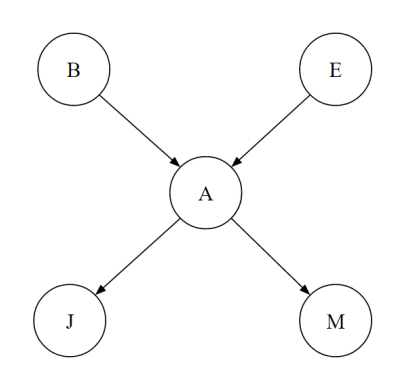
위 베이즈 넷을 통해 간단히 조건부 확률을 표현할 수 있다. $P(B), P(E), P(A|B,E), P(J|A), P(M|A)$가 그렇다. 체인 룰(chain rule)을 통해 더 풀어쓸 수도 있다.

$P(X_1,X_2,...,X_n)=\prod^n_{i=1}P(X_i|parents(X_i))$를 통해 $P(J|A)$를 $P(J|B,E,A)$ 등으로 표현할 수 있다. 그런데 이때 $P(J|B,E,A)=P(B)\cdot P(E) \cdot P(A|B,E) \cdot P(J|A)$임을 확인하자. 각 조건부 확률의 곱에서 자식 노드와 곱해지는 건 그 노드의 부모 노드라는 점 말이다.

정리하자면, 베이즈 넷은 이렇게 구성된다.

• 변수 $X$를 표시하는 노드로 이루어진 사이클이 없는 방향 그래프

• 노드 $X$의 부모 노드를 통해 표시한 조건부 확률 $P(X|A_1...A_n)$.

이때 $A_i$는 $X$의 $i$번째 부모로 조건부 확률 테이블(conditional probability table, CPT)에 저장된다. 이 CPT는 부모 변수 $A_1...A_n$ 확률 $n$개, $X$ 확률 1개, $X$의 조건부 확률 1개 총 $n+2$개의 열을 가진다.

Bayes Nets (Inference)

이미 관측한 에비던스 변수를 통해 쿼리 변수에 대한 결합 확률 분포를 계산하는 과정을 추론(inference)라고 한다. 열거를 통한 추론(inference by enumeration) 방법은 간단하지만 메모리 낭비가 심하다. 하나씩 변수를 제거해가면서 쿼리 변수를 구해보자.

1. $X$를 포함한 모든 요소(factor)를 곱한다.
2. $X$에 대한 합을 구한다(sum out).

이때 factor는 $X$를 포함한 요소는 정규화하지 않은 확률(unnormalized probability)이기 때문에 정규화하기 전까지는 총합이 1이 되지 않을 수도 있다.

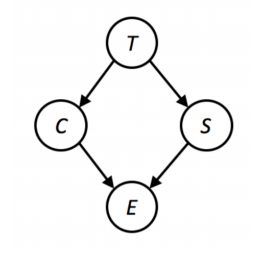
위 베이즈 넷에서 찾을 수 있는 확률 분포 factor는 $P(T), P(C|T), P(S|T), P(E|C,S)$다. $P(T|+e)$을 구하려면 어떻게 해야할까? $C, S$ 등 원하는 변수만 남기고 변수를 없애면서(eliimate variables) 구해보자.

1. $C$를 포함한 모든 확률 요소를 결합(join, multiply)하자. 즉 $P(C,+e|T,S)=P(C|T) \cdot P(+e|C,S)$
2. $C$를 중심으로 합하자. 즉 $P(+e|T,S)$
3. $C$가 사라졌다. $S$를 포함한 모든 확률 요소를 결합한다. $P(+e,S|T)=P(S|T) \cdot P(+e|T,S)$
4. $S$를 중심으로 합하면 $P(+e|T)$가 남는다.

$P(+e|T)$를 통해 $P(T|+e)$를 쉽게 구할 수 있다.

이를 수식으로 표현해보자. $P(T)\sum \limits_{s} P(s|T) \sum \limits_{c} P(c|T) P(+e|c,s)$

Bayes Nets (Sampling)

쿼리를 구할 때 정확한 확률 계산이 아니라 샘플링 추출을 할 수도 있다. 원하는 확률 분포가 있다면, 해당 분포에 대한 샘플을 생성하면서 그 분포를 파악해보는 것이다.

가령 $P(T|+e)$를 구하고 싶을 때 시뮬레이터를 통해 샘플 값을 보는 것만으로 이 분포를 얻어낼 수 있다.

$T$와 $C$부터 먼저 샘플링해보자.

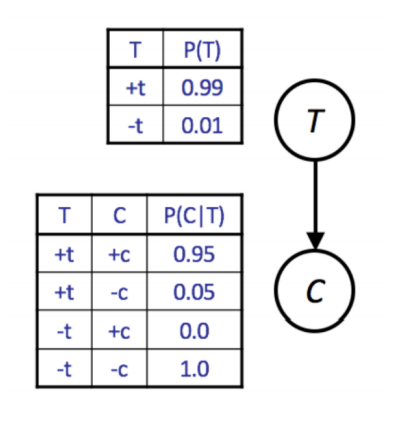
이 샘플을 얻어내는 파이썬 코드는 이렇다.

import random

def get_t():
	if random.random() < 0.99: return True
    return False
def get_c(t):
	if t and random.random() < 0.95: return True
    return False
def get_sample():
	t = get_t()
    c = get_c(t)
    return [t, c]

[t, c]가 곧 $P(T), P(C|T)$를 얻어내기 위한 각 샘플 값이다. 이런 샘플링 기법을 사전 확률 샘플링(prior sampling)이라고 한다. $P(C|-t)$를 얻어내려면 얻어낸 샘플의 99%를 낭비해야 한다는 단점이 있다.

에비던스와 일치하지 않은(inconsistent) 샘플을 미리 받아들이지 않는 샘플링(rejection sampling)을 통해 낭비를 줄일 수 있다.

예를 들어 $P(C|-t)$를 위한 샘플을 추출할 때 $t$가 거짓일 때에만 받아들이면 된다. 물론 이때에도 에비던스에 맞지 않은 샘플을 만들어내는 시간을 낭비하기는 하지만, 이전보다는 시간이 덜 걸린다. 이 두 가지 방법으로 만들어진 샘플 생성 확률은 CPT를 따른다.

좀 더 세련된 방법은 가능도에 가중치를 주는 방법(likelihood weighting)이다. 이 방법을 통해 에비던스와 일치하지 않은 샘플(bad sample)은 절대 만들어내지 않는다고 보장할 수 있기 때문이다.

에비던스와 일치하지 않는 샘플을 만들어내는 건 시간적으로 비효율적이다. 그렇다면 에비던스와 일치하는 데이터만, "그렇다고 설정한 뒤" 샘플링해보면 어떨까?

예를 들어 $P(C|-t)$를 얻어내고 싶을 때에는 간단하게 $T$가 거짓이라고 세팅해보자. 하지만 $T$가 참일 수도 있기 때문에 실제 분포와는 일치하지 않은(inconsistent) 여러 샘플이 만들어진다는 단점이 있다. $P(T,S,+c,+e)$를 계산할 때 $c=false$나 $e=false$인 경우를 고려하지 않는다면 이를 통해 얻어진 샘플이 실제 베이즈 넷의 결합 확률 분포와 맞지 않을 수도 있기 때문이다.

즉 이 방법은 에비던스 변수 $E_1...E_m$을 고정한 뒤 변수 $Z_1...Z_p$를 샘플링하는 기법이다. 이때 샘플은 $P(Z_1...Z_p,E_1...E_m)=\prod_i^p P(Z_i)|Parents(Z_i)$ 확률을 따른다. 이때 샘플이 모든 $P(E_i|Parents(E_i))$을 포함하지는 않는다는 점을 주의해야 한다.

이때 가능도에 가중치를 주는 방식으로 이 문제를 풀 수 있다. 모든 샘플을 똑같이 카운팅하지 말고, 샘플 $j$에 대한 가중치 $w_j$를 샘플링했을 때 에비던스 변수를 관측한 값이 얼마나 많이 나타나는지 보여주는 값이라고 정의하자.

베이즈 넷에 존재하는 모든 변수를 반복해가면서 에비던스 변수가 아니라면 그 변수를 샘플링, 에비던스 변수라면 가중치를 바꾸자.

$P(T|+c, +e)$를 계산할 때 $j$번째 샘플을 구하는 과정은 다음과 같다.

1. $w_j=1, c=true, e=true$로 세팅한다.
2. $T$에 관해서는 에비던스가 없기 때문에 $P(T)$에서 샘플 $t_j$를 구한다.
3. $C$에 관해서는 에비던스가 있다. $P(+c|t_j)$로 샘플링 가중치를 곱하자. $w_j=w_j \cdot P(+c|t_j)$
4. $S$에 관해서 에비던스가 없기 때문에 $P(S|t_j)$에서 샘플 $s_j$를 구한다.
5. $E$에 관해서는 에비던스가 있다. $P(+e|+c,s_j)$로 가중치를 곱한다. $w_j=w_j \cdot P(+e|+c,s_j)$

초깃값 1 대신 가중치 $w_j$로 $j$를 곱한다. 이 방식으로 구한 마지막 샘플 확률 분포는 앞에서 CPT에 맞지 않았던 부분을 커버할 수 있다.

깁스 샘플링(Gibbs Sampling) 또한 샘플링 기법 중 하나다. 모든 변수를 완전히 랜덤한 변수로 세팅하고, 반복적으로 한 번에 변수 하나를 골라 변수를 지우자(clear). 그리고 지금 다른 모든 변수에 할당된 값에 따라서 다시 샘플링한다.

$T,C,S,E$를 다룰 때 모든 변수를 랜덤으로 할당한다. 예를 들어 $t=true, c=true, s=false, e=true$로 세팅하자. 그 뒤 예를 들어 $S$를 뽑아 지우고, $P(S|+t,+t,+e)$ 확률 분포에서 변수 하나를 뽑을 수 있다. 다른 모든 변수 세팅이 주어질 때 변수 하나에 대한 확률 분포를 계산하는 것이다. $S$와 연결된 CPT만을 사용해서 $P(S|T,C,E)$를 계산할 수 있다.

깁스 샘플링을 통해 베이즈 넷을 통해 선형 시간 안에 원하는 변수와 연결된 다른 변수를 사용하면서 조건부 확률 분포를 구할 수 있다. 충분히 많이 깁스 샙플링을 반복한다면, 궁극적으로 올바른 확률 분포에 수렴할 수 있다.