
- 다음 내용은 [CS-188] Introduction to Aritificial Intelligence, UC Berkeley, Fall 2018의 Readings-Note6을 정리하였음을 밝힙니다.
- 스스로 이해하기에 영문 용어가 이해하기 직관적이면 그대로 사용했습니다.
Bayes Nets (D-Separation)
랜덤 변수 집합 중 특정 변수가 다른 변수와 독립적인지 확인해보자. 또는 랜덤 변수 하나가 다른 랜덤 변수가 주어진 상황에서 조건적으로 독립적인지 확인해보자.
베이즈 넷은 결합 확률 분포를 표현하는 베이즈 넷의 특성 덕분에 변수 간의 의존 관계를 빠르게 구할 수 있는데, 이를 D-Separation이라고 한다.
- 노드는 모든 부모 노드가 주어질 때 그래프 상에 존재하는 모든 조상 노드와 조건적으로 독립적이다.
위 정리를 참고하면서, 간선 두 개로 연결된 베이즈 넷의 트리플(triple)이 어떻게 조건적으로 독립적인지 살펴보자.
1. Causal Chains
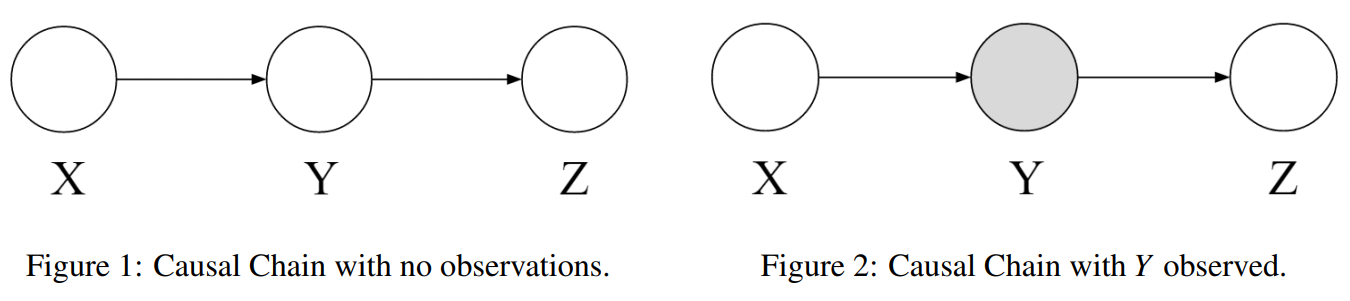
위 그래프에서 부모 노드는 를 통해 자식 노드를 가리킨다. 세 노드는 아무런 관측하지 않은 상태에서 왼쪽 상황과 같다. 이를 결합 분포 확률을 통해 표현해보자.
가 주어질 때 이 조건을 기반으로 가, 그리고 를 기반으로 를 얻을 수 있음을 간단히 볼 수 있다. 그런데 이때 과연 와 가 독립적인지는 아직 모른다.
이때 에 대한 관측을 통해 , 가 조건적으로 독립적이라고 할 수 있다.
자세한 정리는 다음과 같다.
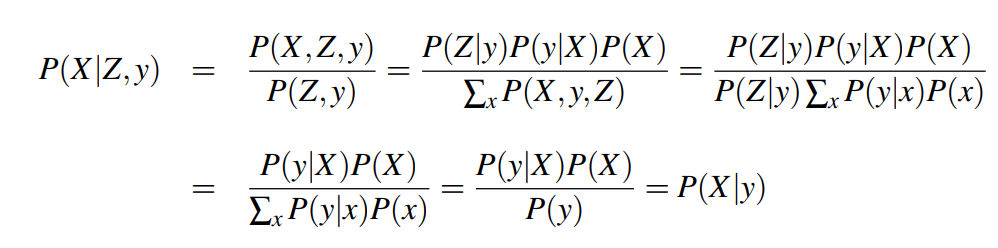
- 노드 자신을 라 하자. 이때 의 부모 노드 와 의 자식 노드 는 를 알게 된다면 조건적으로 독립적이다.
2. Common Cause
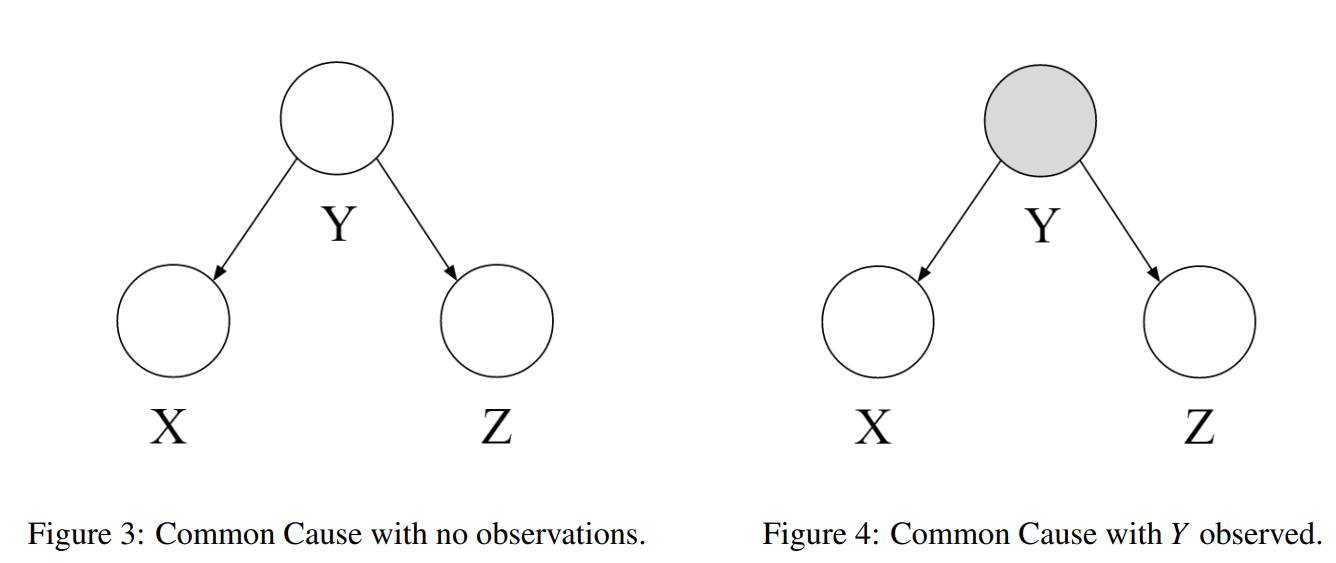
트리플의 또 다른 구조는 로 표현된다. 위 트리플에서 회색으로 칠해진 가 관측된 노드다.
식이 간단하니 이를 확인해보자.
베이즈 정리를 활용한 식 전개를 통해 조건부 독립 관계를 확인할 수 있다.
- 두 노드의 부모 노드 가 관측될 때 의 자식 노드 와 는 각각 조건부 독립적이다.
3. Common Effect
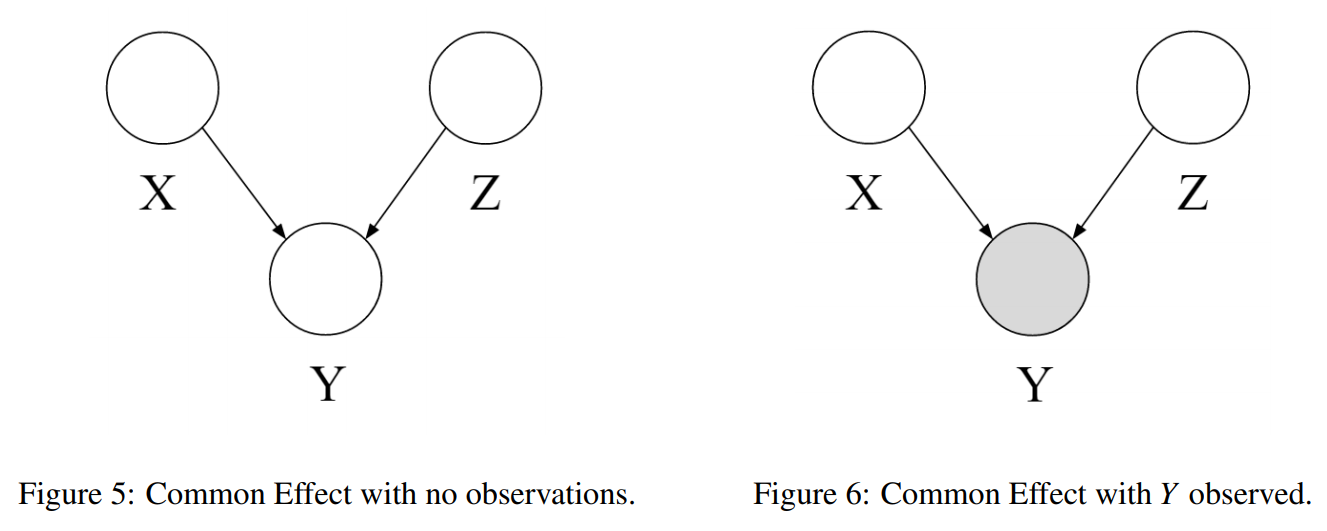
이번에는 부모 노드가 두 개인 자식 노드 가 관측되었을 때 이 자식 노드의 부모 노드인 $X%와 $Y%의 관계를 표현한 트리플이다.
값이 관측되기 전에는 와 는 서로 독립적이다. 그런데 이 자식 노드가 관측된 이후에는 독립적인 관계가 아니게 될 수도 있다.
와 가 불리언 변수고 가 AND 연산의 값이라고 하자. 를 모를 때에는 부모 노드 값을 추론할 근거가 없으나, 값이 참인지 거짓인지 알게 된다면 부모 노드가 어떤 값을 가질지 추론할 수 있게 된다.
- 두 노드의 자식 노드 가 관측될 때 의 부모 노드 와 간의 독립성을 보장할 수 없다. 즉 를 모른다면 와 는 조건적으로 독립적이다.
4. General Case, and D-Separation
위 조건을 보다 일반화한 상황에 적용해보자. 즉, 베이즈 넷 그래프에서 관측값 가 있을 때 와 는 조건부 독립 관계인가? 이 문제를 풀기 위해 사용하는 게 D-Spearation이라는 베이즈 넷의 특성이다.
- D-Separation(directed separation): 관측값 노드 집합 이 두 노드 와 를 직접 분리(d-separates)할 때 이 두 노드는 조건부 독립 관계다.
대략적인 알고리즘은 다음과 같다.
- 관측값 노드 집합 를 마킹한다.
- 마킹되지 않은 노드 중 에서 로 가는 경로 상의 노드가 존재한다면 와 는 연결 관계다.
- 연결 관계인 두 노드는 상에서 조건부 독립 관계가 아니다.
그런데 이 알고리즘은 위 트리플 케이스 중 Common Effect가 없어야만 참이다. 부모 노드 두 개 이상을 가진 자식 노드 가 관측값 노드 집합 에 존재한다고 생각해보자. Common Effect 트리플에 따르면 이때 와 (관측값 집합과는 다른 부모 노드 중의 하나) 간의 조건부 독립 관계는 깨진다. 그런데 위 알고리즘에서는 가 마킹되어 있기 때문에 와 의 연결 관계가 깨진다는 결론이 나온다. 따라서 연결 관계가 깨진 두 노드는 조건부 독립 관계라는 위 알고리즘의 결론은 Common Effect 형태의 트리플이 그래프 내에 없어야만 성립된다.
D-Separation은 Common Effect까지 모두 적용 가능한 알고리즘이다.
- 관측값 노드 집합 를 마킹한다.
- 에서 로 가는 모든 양방향 경로를 열거해보자.
- 각 경로에 대해서 경로를 트리플로 쪼개고,
모든트리플이 활성화되어 있는지 확인한다. 이때 모든 트리플이 활성화되어 있다면 와 를 직접 연결시킨다. 이때 직접 연결시키는(direct connect) 과정이 핵심이다. - 모든 경로 상에서 d-connection이 없다면 이 경로 상에서 와 는 d 분리되어 있다. 즉 와 는 가 주어진 상황에서 조건적으로 독립 관계다.
-
트리플을 구성하는 중간 노드 가 관측된 여부에 따라 , 가 조건적으로 독립 관계라면, 이 트리플은 활성화(active) 상태가 아닌 비활성화(inactive) 상태다.
-
주어진 다수의 경로 중 경로를 구성하는 모든 트리플이 활성화되어 있다면 와 를 d 분리하는 경로 하나가 나온다. 이런 경로를 활성화된 경로라고 하자. 주어진 모든 경로가 비활성화되어 있다면 와 가 독립적이다.
트리플의 세 가지 케이스 가운데
Common Effect는 가 관측되어야 와 의 독립 관계를 보장할 수 없는, 활성화 상태라는 데 주의하자.
5. Examples
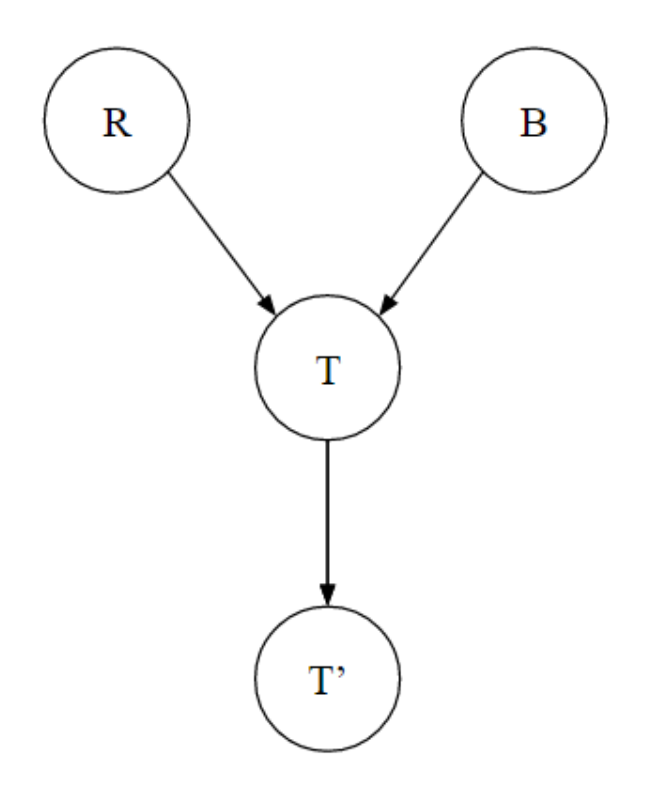
, 가 각각 관측값으로 주어질 때 다른 두 노드의 독립성을 보장할 수 있는지 확인해보자.
- : 가 관측되지 않았기 때문에 활성화된 트리플이 없다. 따라서
d-connection이 없으므로, 독립 관계를 보장할 수 있다. - : 가 관측되었기 때문에
Common Effect구조의 트리플이 활성화되었고, 이 트리플이 경로를 쪼갠 트리플 중에 존재하기 때문에 과 를 연결하는d-connection이 존재한다. 독립 관계를 보장할 수 없다. - : 가 관측되었다. 2번과 마찬가지로 가 의 자식 노드이므로
Common Effect트리플이 적용된다. 독립 관계를 보장할 수 없다. - : 가 관측되었을 때 에서 로 연결되는 경로 트리플이 비활성화된다. 독립 관계를 보장할 수 있다.
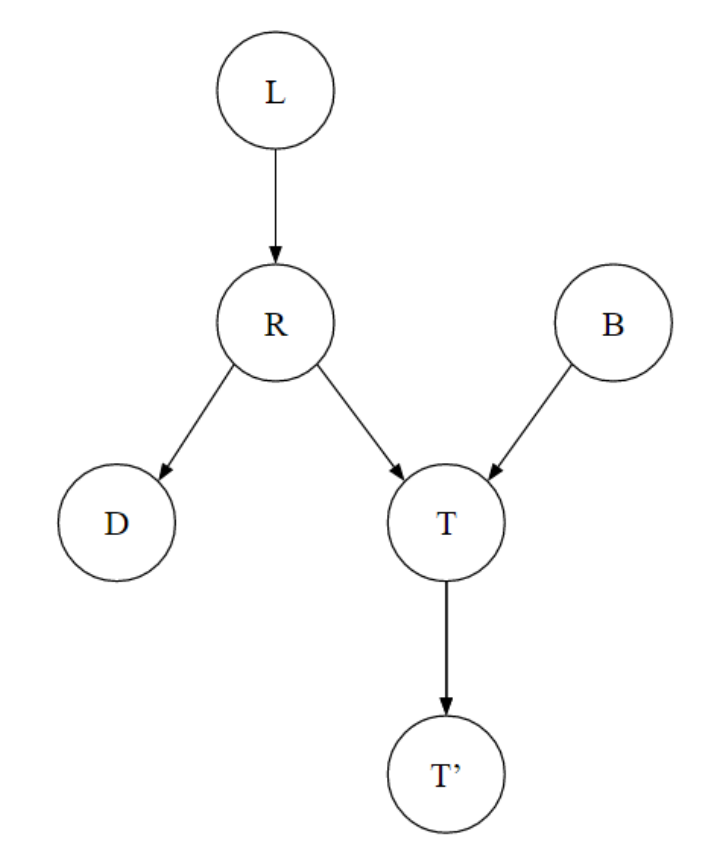
- : 관측을 통해
Causal Chain관계에서 트리플이 비활성화된다. 독립성을 보장할 수 있다. - : 트리플 는 활성화 트리플이지만 가 비활성화 트리플이기 때문에 독립성이 보장된다.
- : 2번과 달리 또한 활성화되었기 때문에
d-connection이 발생한다. 독립성을 보장할 수 없다. - : 가 의 자식 노드이고 가
Common Effect트리플의 중간 노드이자 경로를 구성하는 트리플 중 하나이므로d-connection이 발생했다. 즉 독립성을 보장할 수 없다. - : 독립성이 보장된다.
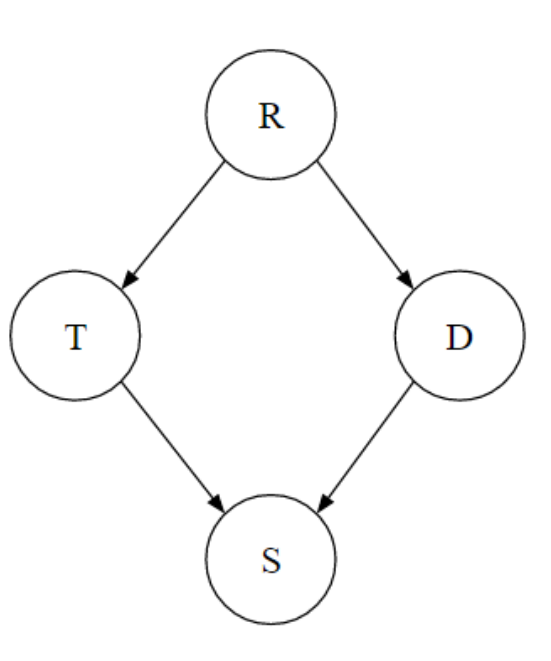
- : 경로를 구성하는 트리플 가
Common Cause케이스 중 가 관측되지 않아 활성화되었다. 이 경로가 활성화되었기 때문에 독립성을 보장할 수 없다. - : 이 관측되었기 때문에 모든 경로를 구성하는 트리플이 비활성화되었다. 독립성을 보장할 수 있다.
- : 가 관측되었을 때 관측으로 인해
Cmmon Cause가 활성화되었기 때문에 독립성을 보장할 수 없다.
D-Separation을 통해 베이즈 넷에 표현된 노드 간의 조건부 독립 관계를 빠르게 파악할 수 있다. 이를 통해 베이즈 넷 추론 및 샘플링에 활용할 수 있다.
