• 다음 내용은 [CS-188] Introduction to Aritificial Intelligence, UC Berkeley, Fall 2018의 Readings-Note8을 정리하였음을 밝힙니다.
• 스스로 이해하기에 영문 용어가 이해하기 직관적이면 그대로 사용했습니다.

Viterbi Algorithm

히든 마르코브 모델을 풀 때 지금까지 관측값을 얻은 에비던스가 주어질 때 히든 변수는 어떤 차례로 이루어져 있을지 질문을 던질 수 있다. 즉 $argmax_{x_{1:N}}P(x_{1:N}|e_{1:N})=argmax_{x_{1:N}}P(x_{1:N},e_{1:N})$를 풀자.

지금 가지고 있는 에비던스의 관측값으로 이어지는 가장 높은 확률의 히든 상태가 무엇일지 동적 프로그래밍을 통해 얻어낼 수 있다.

비터비 알고리즘(Viterbi Algorithm)은 다음과 같은 단계를 밟는다.

1. 타임 스탬프 t까지 관측값을 얻은 에비던스가 주어질 때, 타임 스탬프 t=i의 $(state, time)$에 대한 최적의 경로를 얻을 확률을 연산하자.
2. 가장 큰 확률 경로 상에 존재하는 터미널 노드를 찾고, 그 상태로 이어지는 최고의 경로를 거꾸로 순회하면서 얻어낸다.

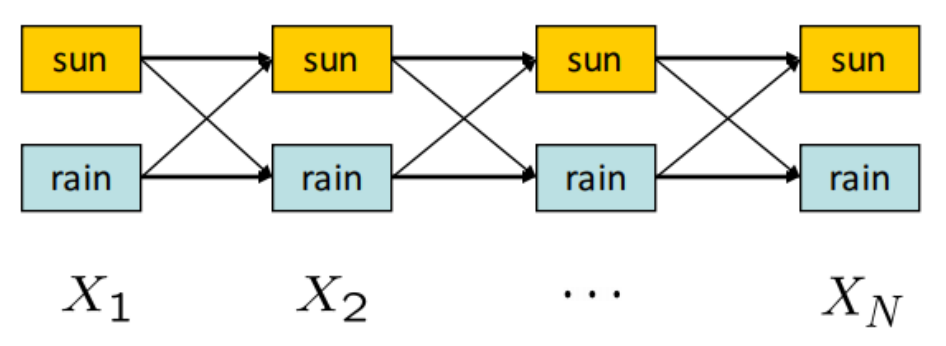
위 HMM에서 히든 상태는 총 두 개다. 날씨가 맑거나 비가 오는 경우로, 타임 스탬프 t=1,2,...,N까지 어떤 상태를 얻느냐에 따라 화살표를 택할 수 있다.

간선의 가중치를 $P(X_t|X_{t-1})P(E_t|X_t)$로 구할 수 있다. $P(X_t|X_{t-1})$이 어떤 트랜지션을 택했는지, $P(E_t|X_t)$은 결과로 얻은 상태가 어떤 에비던스의 관측값을 가지고 있는지 보여준다. 추가로, 경로를 얻을 확률은 이 간선을 계속해서 곱한 값이다.

앞에서 비터비 알고리즘을 통해 구할 수식을 표현해보자.

• $P(x_{1:N}|e_{1:N})=P(X_1)P(e_1|X_1)\prod\limits_{t=2}^{N}P(X_t|X_{t-1})P(e_1|X_t)$

• $P(X_N,e_{1:N}=\sum\limits_{x_1,...,x_{N-1}}P(X_N,x_{1:N-1,e_{1:N}}))$

• $argmax_{x_1,...,x_N}P(x_{1:N},e_{1:N})$

$P(x_{1:N},e_{1:N})$ 값을 가장 크게 만들 수 있는 ${x_1,...,x_N}$를 구하는 비터비 알고리즘

비터비 알고리즘을 결합 확률 분포 테이블을 통해 구하기 위해서는 모든 가능한 히든 상태에 대한 연산을 하면 된다. 하지만 이 경우 연산 비용이 매우 크기 때문에 동적 프로그래밍을 통해 연산량을 절약할 수 있다.

• $m_t[x_t]=max_{x_{1:t-1}}P(e_t|x_t)P(x_t|x_{t-1})P(x_{1:t-1,e_{1:t-1}})=P(e_t|x_t)max_{x_{t-1}}P(x_t|x_{t-1})max_{x_{1:t-2}}P(x_{1:t-1},e_{1:t-1})=P(e_t|x_t)max_{x_{t-1}}P(x_t|x_{t-1})m_{t-1}[x_{t-1}]$

즉 비터비 알고리즘의 재귀적 동적 프로그래밍을 통해 효율적으로 가장 확률이 높은 경로로 이어지는 마지막 상태 $x_N$을 구할 수 있다. 전체 경로를 구하려면 백트래킹을 한 번 더 해야 한다.

• $a_t[x_t]=P(e_t|x_t)argmax_{x_{t-1}}P(x_t|x_{t-1})m_{t-1}[x_{t-1}]=argmax_{x_{t-1}}P(x_t|x_{t-1})m_{t-1}[x_{t-1}]$

위 $a_t[x_t]$를 통해 $x_t$로 이어지는 최고의 경로를 만드는 마지막 트랜지션이 무엇인지 백트래킹할 수 있다.

배열 $a$는 $N$개의 시퀸스를 담고 있는데, 각 시퀸스 하나는 목적 상태 $x_N$으로 이어지는 가장 그럴 듯한 시퀸스 정보다.

비터비 알고리즘을 통해 다항식 시간 안에 주어진 에비던스를 설명하는 가장 그럴 듯한 확률 분포를 얻을 수 있다.