• 다음 내용은 [CS-188] Introduction to Aritificial Intelligence, UC Berkeley, Fall 2018의 Readings-Note8을 정리하였음을 밝힙니다.
• 스스로 이해하기에 영문 용어가 이해하기 직관적이면 그대로 사용했습니다.

Hidden Markov Models

마르코프 모델을 통해 특정 타임 스탬프 t가 주어졌을 때 그 시점의 랜덤 변수의 값을 빠르게 계산할 수 있다. 초깃값과 트랜지션 모델만 주어진다면 단순 연산의 반복이기 때문이다. 하지만 연산 도중 트랜지션 모델에 영향을 미칠 변수가 생긴다면 어떻게 해야 할까?

히든 마르코프 모델(hidden Markov models)을 통해 각 타임 스탬프의 에비던스 관측값을 얻을 수 있다. 이 에비던스가 각 상태 노드(즉 랜덤 변수의 타임 스탬프 t에서의 값)에 얼마나 영향을 미치는지 알 수 있다.

마르코프 모델이 각 상태에서의 랜덤 변수만을 필요로 했다면, 히든 마르코프 모델은 그 타임 스탬프에서의 랜덤 변수를 가리키는 에비던스 변수를 가진다.

다음은 각 타임 스탬프에서의 날씨 값인 상태 변수 $W$(state variables)와 이에 대한 에비던스 변수 $F$(evidence variable)로 표현된 히든 마르코프 모델이다.

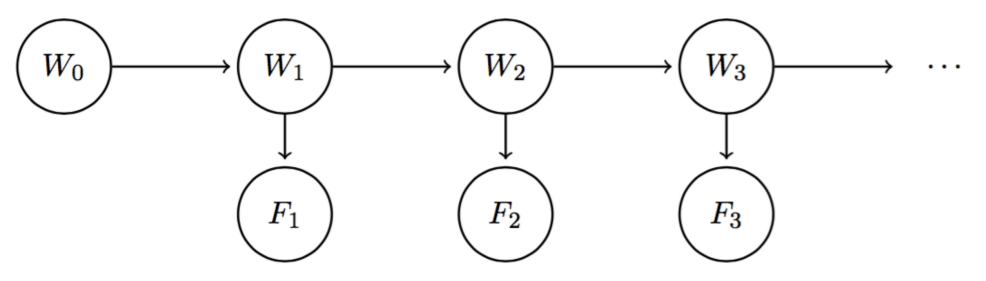
이때 $W$는 타임 스탬프 t=i에서 날씨가 어떨지 확률적으로 보여주는 일종의 믿음(belief)으로부터 값이 구성되었다. 그렇기 때문에 이 믿음이야말로 에비던스와 조건부 확률 관계가 있다.

$F_1 \perp W_0|W_1$
$\forall i=2,...,n;\; W_i\perp{W_0,...,W_{i-2},F_1,...,F_{i-1}}|W_{i-1}$
$\forall i=2,...,n;\; F_i\perp{W_0,...,W_{i-1},F_1,...,F_{i-1}}|W_i$

마르코프 모델과 마찬가지로 히든 마르코프 모델 역시 트랜지션 모델 $Pr(W_{i+1}|W_i)$이 특정 타임 스탬프에서 수렴하리라는, 정상(stationary) 특성을 가지는데, $Pr(F_i|W_i)$ 또한 그렇다. 이 같은 확률 변수(상태 변수를 기반으로 한 에비던스 변수 조건부 확률)을 특히 센서 모델(sensor model)이라고 부른다.

센서 모델을 기존의 초깃값 확률 분포, 트랜지션 모델에 추가해서 빌리프 분포를 정의할 수 있다. 이때 빌리프 분포란 타임 스탬프 t=i까지 모두 모은 에비던스가 있을 때 상태 변수 값이 나올 조건부 확률이다.

$B(W_i)=Pr(W_i|f_1,...,f_i)$

t=i에서의 에비던스 $f_i$를 쓰지 않을 때의 빌리프 분포 $B'(W_i)$는 다음과 같다.

$B'(W_i)=Pr(W_i|f_1,...,f_{i-1})$

일반적으로 에비던스를 $e$라고 적고, t=1부터 t=i까지의 모든 에비던스를 이렇게 표현하자.

$e_{1:t}=e_1,...,e_t$

이 방식으로 $B'(W_i)=Pr(W_i|f_1,...,f_{i-1})$을 $B'(W_i)=Pr(W_i|f_{1:(i-1)})$로 축약할 수 있다.

The Forward Algorithm

$B(W_i)$와 $B'(W_{i+1})$를 미니-포워드 알고리즘에서 사용한 업데이트 규칙을 통해 합계(marginalization)를 내보자. 두 빌리프 분포의 차이점은 $B(W_i)$은 t=i, $B'(W_{i+1})$은 t=i+1이 에비던스 $f_{1:i}$를 가졌을 때 어떤 조건부 확률을 가지느냐다.

$B'(W_{i+1})=Pr(W_{i+1}|f_1,...,f_i)=\sum\limits_{w_i}Pr(W_{i+1},w_i|f_1,...,f_i)=\sum\limits_{w_i}Pr(W_{i+1}|w_i,f_1,...,f_i)Pr(w_i|f_1,...,f_i)=\sum\limits_{w_i}Pr(W_{i+1}|w_i)B(w_i)$

$t=i+1$까지의 에비던스가 주어질 때 빌리프 분포 $B(W_{i+1})$은 다음과 같다.

$B(W_{i+1})=Pr(W_{i+1}|f_1,...,f_{i+1})=\frac{Pr(W_{i+1},f_{i+1}|f_1,...,f_i)}{Pr(f_{i+1}|f_1,...,f_i)}$

베이즈 규칙과 체인 룰을 통해 $f_{i+1}$을 붙일 수 있었는데, $Pr(W_{i+1},f_{i+1}|f_1,...,f_i)$가 $B(W_{i+1})$ 값을 결정하는 핵심적인 요소다.

그리고 $Pr(W_{i+1},f_{i+1}|f_1,...,f_i)$을 $W_{i+1}$을 기준으로 분리하면 $Pr(f_{i+1}|W_{i+1},f_1,...,f_i)Pr(W_{i+1}|f_1,...,f_i)$이다. 그런데 히든 마르코브 모델에서 에비던스 $f$는 다른 에비던스가 아니라 $W$의 영향만을 받는다.

따라서 $Pr(f_{i+1}|W_{i+1},f_1,...,f_i)$은 $Pr(f_{i+1}|W_{i+1})$와 같다. $Pr(W_{i+1}|f_1,...,f_i)$가 $B'(W_{i+1})$의 정의라는 점에서 다시 이 표현은 $Pr(f_{i+1}|W_{i+1})B'(W_{i+1})$로 축약된다. $B'(W_{i+1})$를 앞에서 재정의한 식으로 표현해서 정리해보자.

$B(W_{i+1})\propto Pr(f_{i+1}|W_{i+1})\sum\limits_{w_i}Pr(W_{i+1}|w_i)B(w_i)$

t=i+1 단계의 빌리프 분포는 t=i 단계의 빌리프 분포를 기반으로 구할 수 있고, 이 반복적인 연산을 포워드 알고리즘(forward algorithm)이라고 한다.

포워드 알고리즘은 두 가지 단계를 통해 구한다.

• 시간에 따른 업데이트 time elapse update: 타임 스탬프 t에 따라 업데이트한다. $B(W_i)$로부터 $B'(W_{i+1})$를 결정한다고도 볼 수 있다. 이때 주어지는 에비던스는 $f_{1:i}$로 같고 t=i만 t+i+1로 달라지기 때문이다.

• 관측값에 따른 업데이트 observation update: 에비던스 $f_{i+1}$가 추가된 업데이트 방식이다. $B'(W_{i+1})$로부터 $B(W_i)$를 구하는 것이다. 타임 스탬프는 달라지지 않는다.

먼저 타임 스탬프에 따른 업데이트를 한 뒤 얻은 $B'(W_{i+1})$을 통해 나머지를 구하며, 이 업데이트가 번갈아 적용된다.

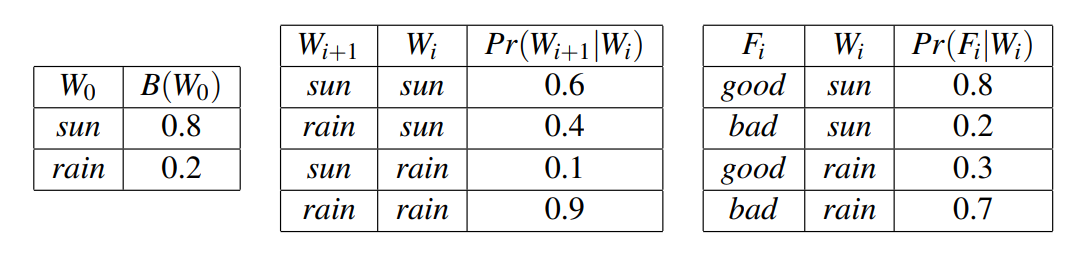
위 분포가 주어질 때 빌리프 분포를 구해보자.

$B'(W_1=sun)=\sum\limits_{w_0}Pr(W_1=sun|w_0)B(w_0)=Pr(W_1=sun|W_0=sun)B(W_0=sun)+Pr(W_1=sun|W_0=rain)B(W_0=rain)=0.6*0.8+0.1*0.2=0.5$
$B'(W_1=rain)=\sum\limits_{w_0}Pr(W_1=rain|w_0)B(w_0)=Pr(W_1=rain|W_0=sun)B(W_0=sun)+Pr(W_1=rain|W_0=rain)B(W_0=rain)=0.4*0.8+0.9*0.2=0.5$

이 빌리프 분포가 비례할 부분을 구해보자.

$B(W_1=sun) \propto Pr(F_1=good|W_1=sun)B'(W_1=sun)=0.8*0.5=0.4$
$B(W_1=rain) \propto Pr(F_1=good|W_1=rain)B'(W_1=rain)=0.3*0.5=0.15$

두 합계인 $0.55$로 $B(W_1)$를 마지널라이즈한다.

$B(W_1=sun)=0.4/0.55=\frac{8}{11}$
$B(W_1=rain)=0.15/0.55=\frac{3}{11}$

에비던스 관측값이 반영되자 날씨가 맑을 때 확률이 증가했고 흐릴 확률이 낮아졌음을 알 수 있다.