Tree

트리의 정의

• 다음과 같은 한 개 이상의 노드의 유한한 집합
• 루트 노드 1개
• 루트의 서브트리

  트리의 재귀적 구조를 이해하자!

트리 관련 용어

• Node: 노드의 정보 + 다른 노드로 향하는 브런치
• Degree: 노드의 서브트리 개수
• Degree of a tree: 트리 내 노드 degree의 최댓값
• Leaf: degree가 0인 노드
• Parent: 서브트리가 있는 노드
• Children: 서브트리의 루트 노드들
• Siblings: 같은 parent를 둔 children
• Ancestor of a node: 해당 노드로부터 루트 노드까지 이어지는 모든 노드들
• Descendants of a node: 해당 노드의 서브트리에 존재하는 모든 노드들
• Level of a node: 노드의 parent 레벨 + 1(루트 노드는 레벨 0 또는 레벨 1로 정의, 일반적으로 1)
• Height/depth: 트리 내 노드가 가지는 레벨의 최댓값

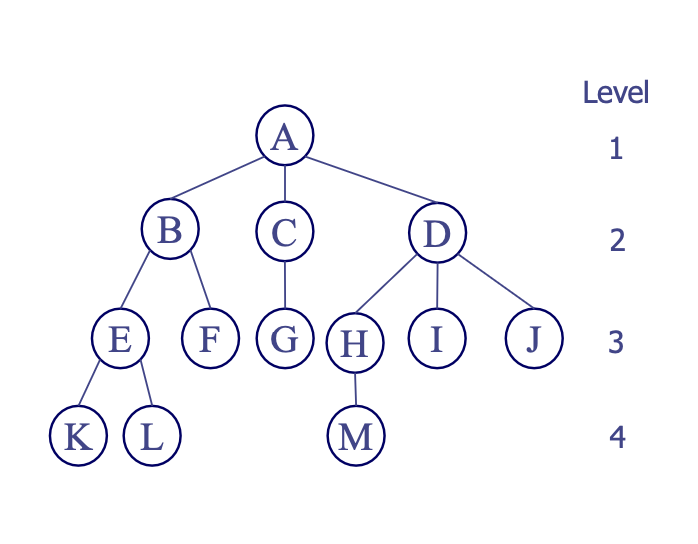
1. 트리의 루트: A
2. A의 Degree: 3
3. Leaf: K, L, F, G, M, I, J
4. D의 Parent: A
5. D의 Children: H, I, J
6. H의 Siblings: I, J
7. 트리의 depth: 4
8. 노드 M의 ancestors: H, D, A
9. 노드 D의 descendants: H, I, J, M

트리 표현 방식

• 서브트리가 리스트로 표현되는 리스트를 통해 트리 표현 가능
• 노드 크기가 고정될 때 트리 표현이 보다 편리 → degree가 고정된다면 노드의 자료 구조에서 메모리 낭비가 심할 수 있기 때문에 제한하는 게 편리
• Left child-right sibling tree: 모든 노드가 최대 한 개의 leftmost child, 한 개의 가장 가까운 right sibling을 가지도록 크기 고정.

트리에서 children의 순서는 중요하지 않기 때문에 특정 노드의 어떤 children이더라도 leftmost할 수 있다!

• Degree Two Tree: Left child-right sibling tree를 시계 방향으로 45도 꺾을 때 시각화할 수 있는 구조
  

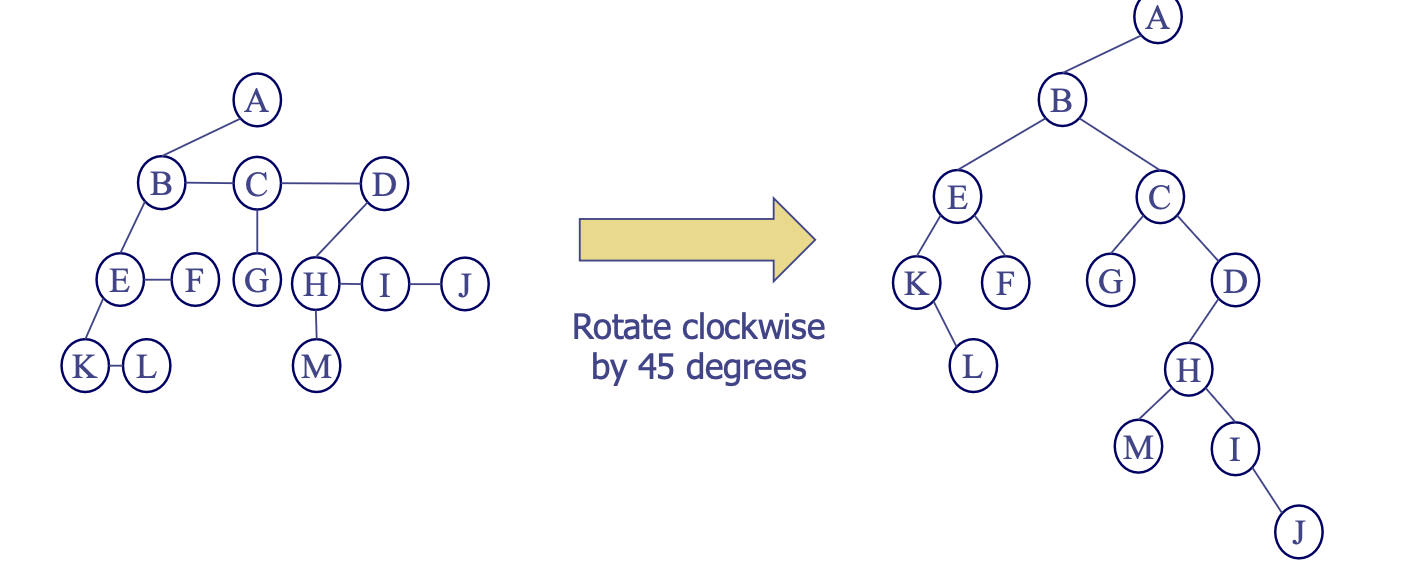
이진 트리

• 노드의 degree가 최대 2를 넘지 않도록 설정된 트리
• 재귀적 정의 - 빈 트리 또는 루트와 좌측 서브트리, 우측 서브트리로 불리는 두 개의 서로소 이진 트리로 구성된 유한한 노드 집합
• Left child-right sibling tree를 통해 표현 가능한 트리로도 표현 가능
  

이진 트리 노드 개수의 최댓값

• 이진 트리는 레벨i에서 최대 $2^{i-1}$ 개 노드를 가진다.
• depth가 k인 이진 트리는 최대 $2^k-1$개 노드를 가진다.

  $\sum^k_{i=1}2^{i-1}=2^k-1$

리프 노드와 degree가 2개인 노드의 관계

• $n_0$이 리프 노드의 개수, $n_2$가 degree가 2인 노드의 개수라면 $n_0=n_2+1$
• 이진 트리를 구성하는 노드의 종류는 degree의 개수에 따라서 $n_0$, $n_1$, $n_2$로 구성된다. 즉 $n=n_0+n_1+n_2$
• 루트 노드를 제외한 모든 노드는 브런치로 연결되어 있기 때문에 브런치 $B$의 개수 $B$에 관해서 $n=B+1$로 표현 가능
• 모든 브런치 $B$의 개수는 degree가 1인 $n_1$에 1개, degree가 2인 $n_2$에 관해 2개이다. 즉 $B=n_1+2n_2$이다.
• $n=B+1=n_1+2n_2+1=n_0+n_1+n_2$ 수식에서 $n_0$에 관해 풀면 $n_0=n_2+1$이다.

정 이진 트리 Full Binary Tree

• depth가 k인 이진 트리의 노드 개수가 $2^k-1$ 개인 이진 트리
  

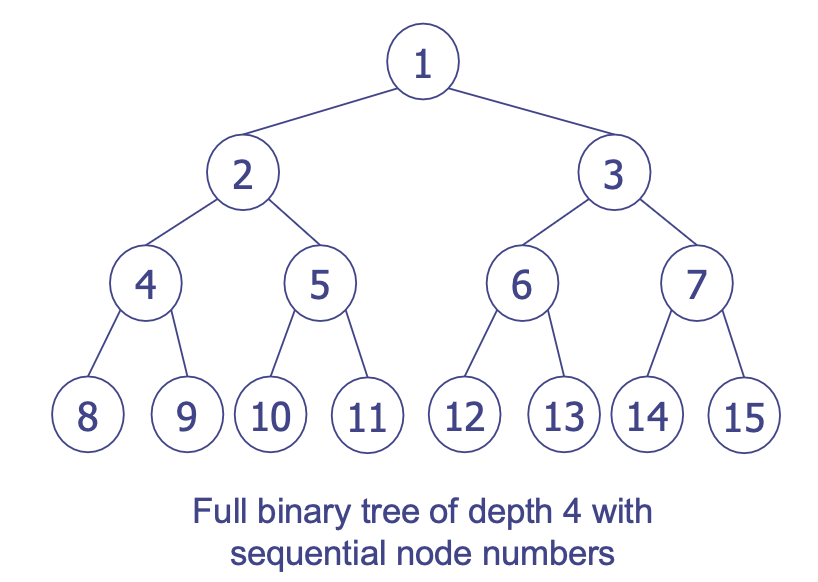
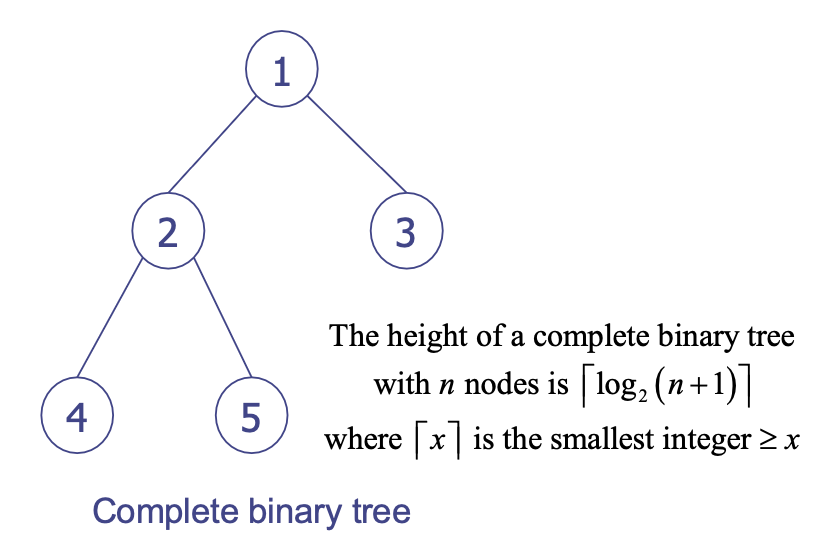
완전 이진 트리 Complete Binary Tree

• 노드 n개가 depth가 k인 정 이진 트리 안에서 노드 n번까지 상응하는 이진 트리
  

이진 트리의 배열 표현

• 배열 인덱스를 통해 parent, children 위치를 현재 노드 위치 i를 통해 찾을 수 있음 → i/2, 2i, 2i+1 세 가지 방식을 통해 표현 (루트 노드는 parent가 없는 예외 존재)
• 메모리 낭비: depth가 k인 휘어진 이진 트리일 경우 필요한 공간 $2^k-1$개에 비해 $k$개만 필요할 수 있음

이진 트리의 연결 리스트 표현

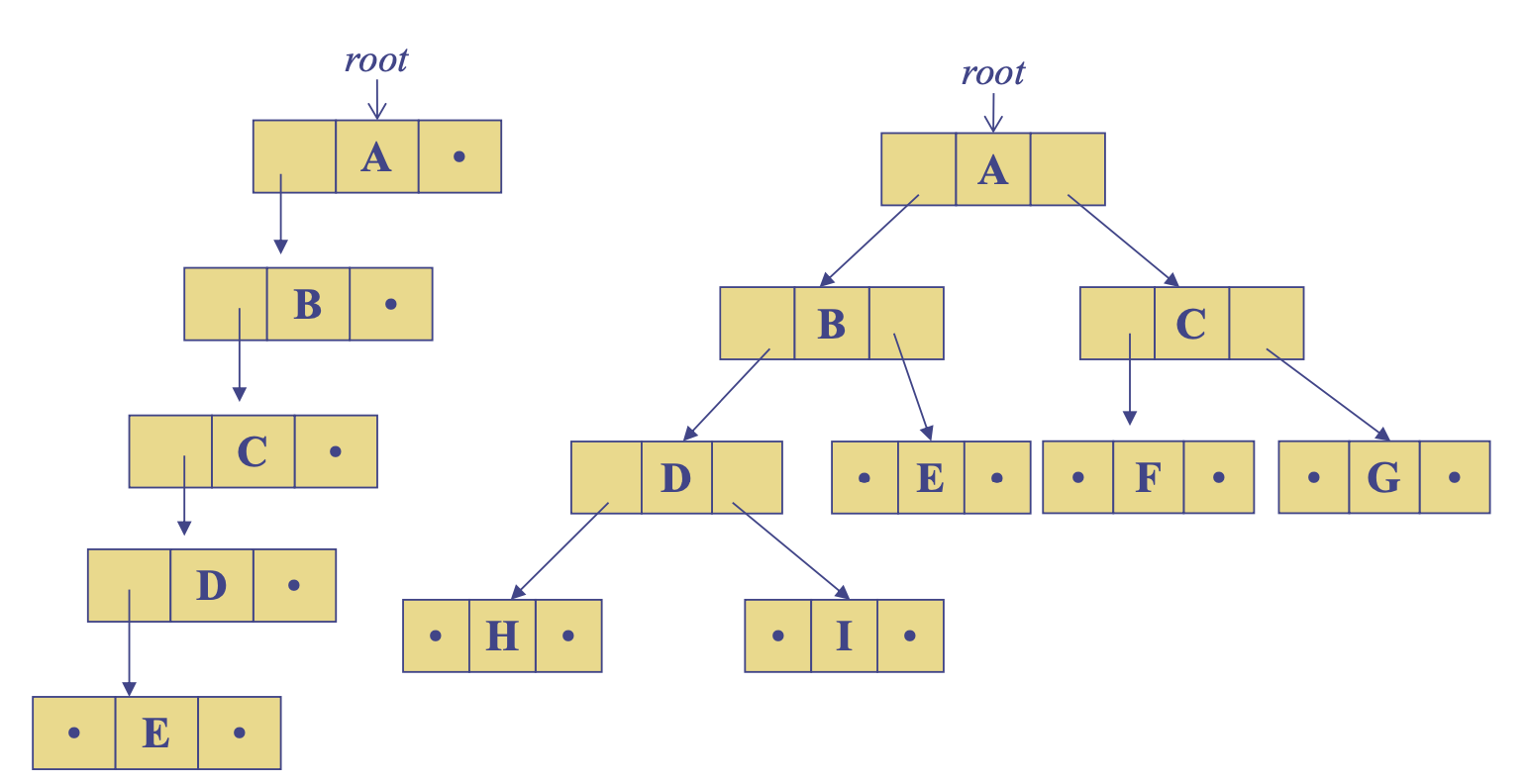
• 연결 리스트를 통한 모든 종류의 '이진' 트리를 효율적으로 표현 가능
• 각 노드는 데이터, 좌측 자식, 우측 자식 세 가지 프로퍼티를 가짐
• 특정 노드의 부모를 찾기 위한 별도의 프로퍼티가 필요할 수 있다는 이슈

이진 트리 순회

• 이진 트리 순회 (루트, 좌측 서브 트리, 우측 서브 트리)를 순회하는 방법에 따라서 순회 방법이 달라짐 → 6가지 순회 방식 존재
• 세 가지 주요한 순회 방법 존재: (1). 중위 (2). 전위 (3). 후위
  

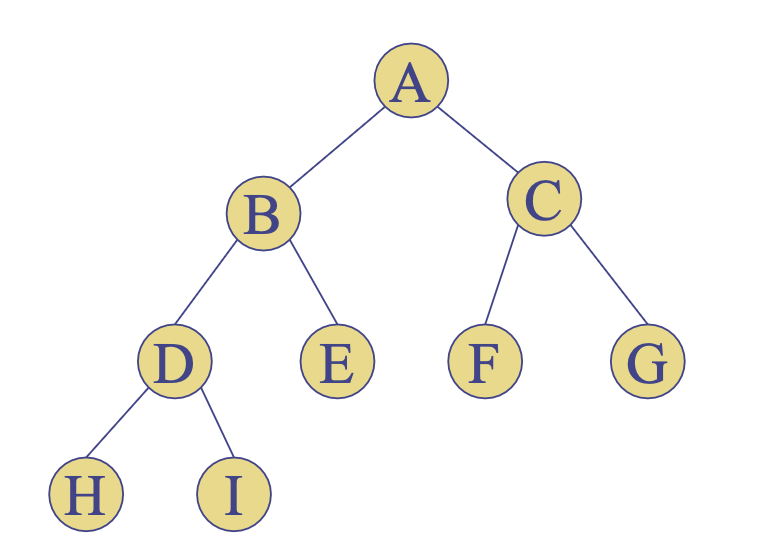
1. Inorder: H-D-I-B-E-A-F-C-G
2. Preorder: A-B-D-H-I-E-C-F-G
3. Postorder:H-I-D-E-B-F-G-C-A

중위 순회

• Inorder traversal
• (1). 갈 수 있는 곳까지 왼쪽을 향해 이동 (2). 노드 방문 (3). 오른쪽으로 노드 한 칸을 옮기고 계속하기. 움직일 수 없다면 한 번 더 다른 노드로 이동하기

import Foundation

let mockTree = ["nil", "A", "B", "C", "D", "E", "F", "G", "H", "I"]

func inorderTraverse(idx: Int) {
    if idx * 2 < mockTree.count {
        inorderTraverse(idx: idx * 2)
    }
    print(mockTree[idx], terminator: " ")
    if idx * 2 + 1 < mockTree.count {
        inorderTraverse(idx: idx * 2 + 1)
    }
}

inorderTraverse(idx: 1)
// H D I B E A F C G

전위 순회

let mockTree = ["nil", "A", "B", "C", "D", "E", "F", "G", "H", "I"]

func preorderTraverse(idx: Int) {
    print(mockTree[idx], terminator: " ")
    if idx * 2 < mockTree.count {
        preorderTraverse(idx: idx * 2)
    }
    if idx * 2 + 1 < mockTree.count {
        preorderTraverse(idx: idx * 2 + 1)
    }
}

preorderTraverse(idx: 1)
// A B D H I E C F G

후위 순회

import Foundation

let mockTree = ["nil", "A", "B", "C", "D", "E", "F", "G", "H", "I"]

func postorderTraverse(idx: Int) {
    if idx * 2 < mockTree.count {
        postorderTraverse(idx: idx * 2)
    }
    if idx * 2 + 1 < mockTree.count {
        postorderTraverse(idx: idx * 2 + 1)
    }
    print(mockTree[idx], terminator: " ")
}


postorderTraverse(idx: 1)
// H I D E B F G C A

스택, 큐를 사용하는 이진 트리 순회

• 반복 중위 순회: 스택 사용
• level order 순회: 큐 사용. 루트를 먼저, 루트의 좌측, 우측을 순서대로 방문함. 새로운 레벨의 leftmost에서부터 rightmost까지 방문

스레디드 이진 트리

• 이진 트리의 링크 → 실제 데이터보다 널 값이 더 많기 때문에 널 링크를 스레드라는 포인터로 대체하는 방법
  
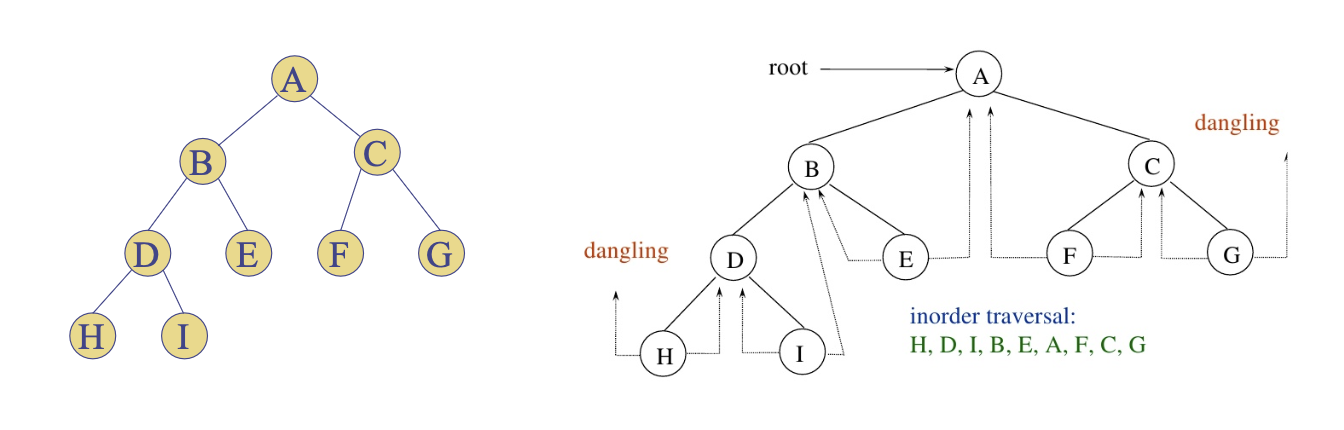
• 좌측 서브트리가 없을 때(=null일 때): 중위 순회 순서 상 현재 노드 이전에 방문하게 될 노드를 대체
• 우측 서브트리가 없을 때(=null일 때): 중위 순회 순서 상 현재 노드 이후에 방문하게 될 노드를 대체
• 스레드 포인터와 정상 포인터 구별 필요: leftThread, rightThread라는 두 개의 추가적인 프로퍼티 필요

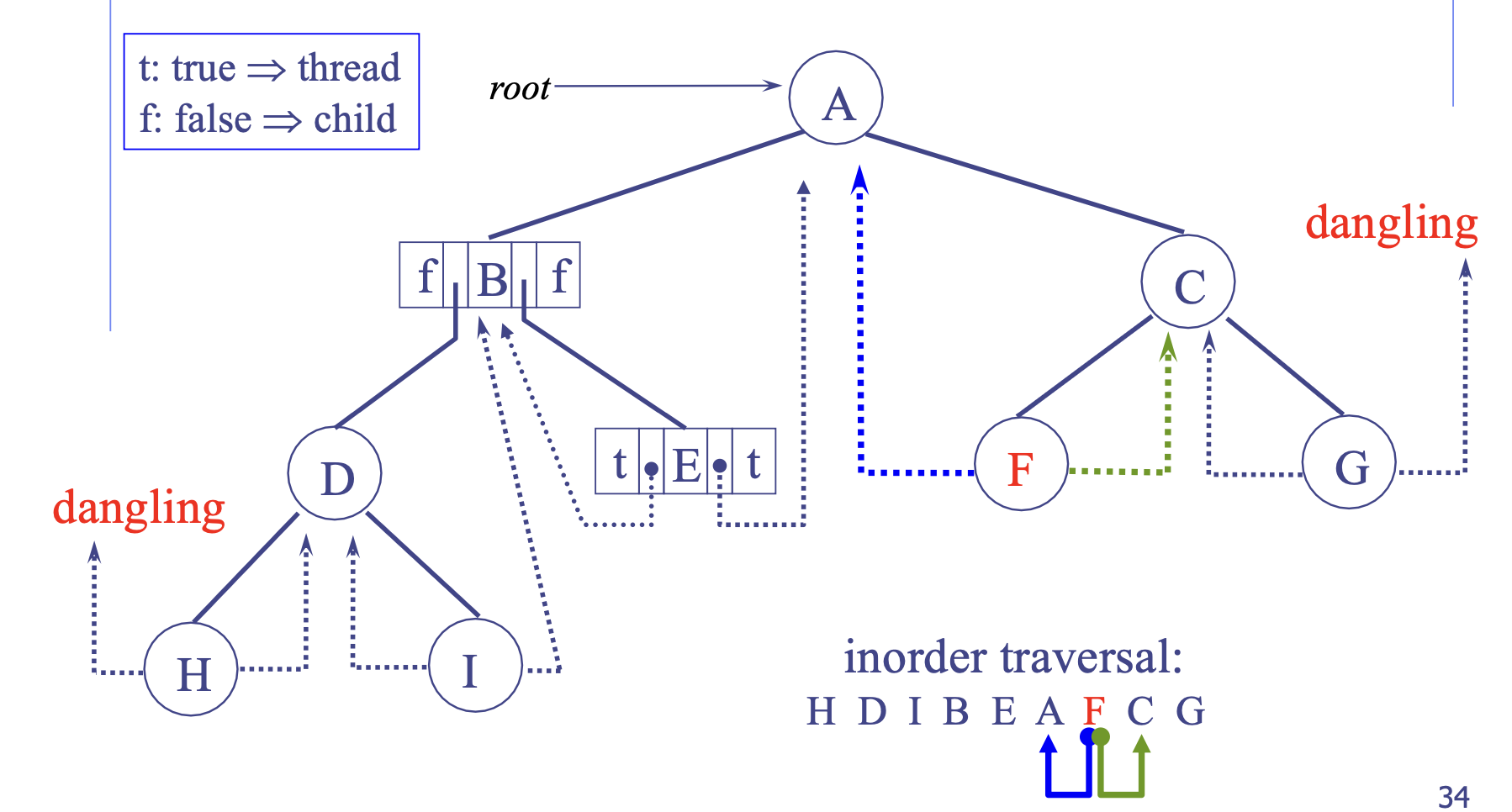
• 널 포인터가 위치할 노드의 위치를 중위 순회 전후를 통해 파악 가능
• 현 시점에서는 중위 순회 순서 상에 전후 노드가 없을 때 연결할 수 없는 링크가 존재(E.g. H의 좌측 leftThread, G의 우측 rightThread)

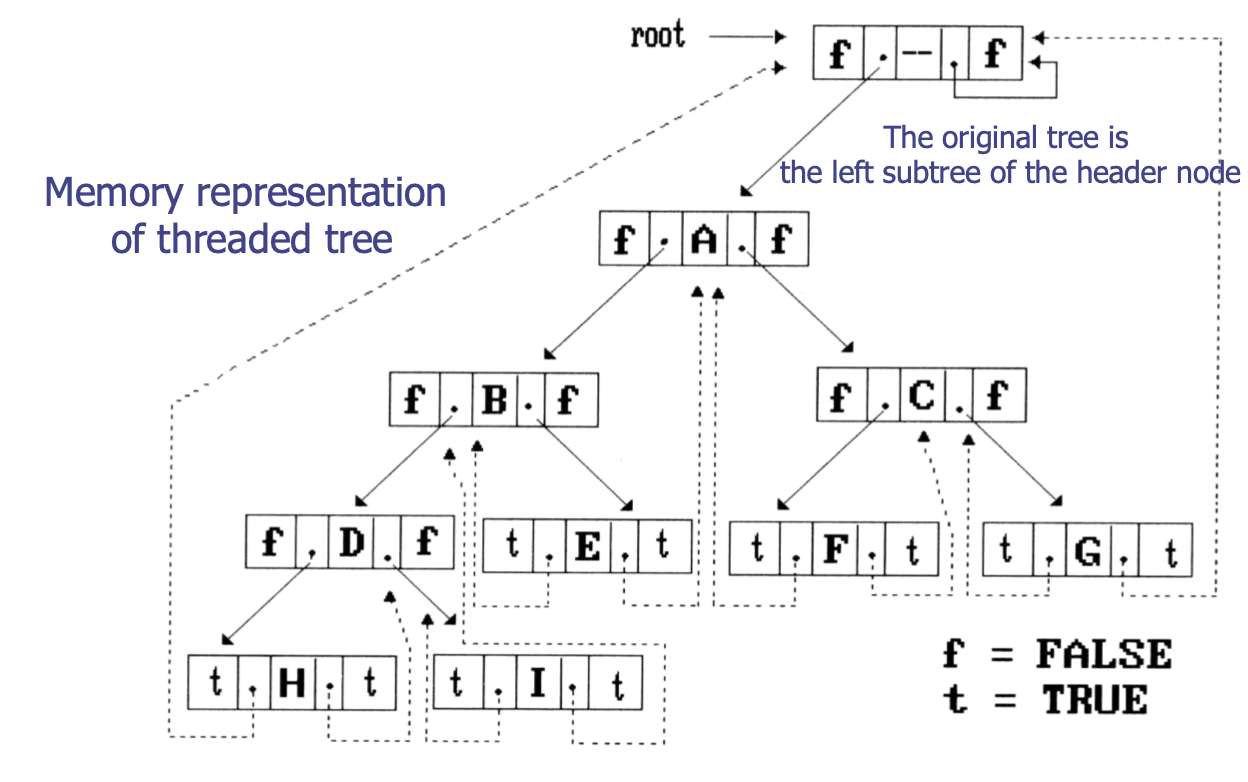
• 연결할 수 없는 링크가 없는 스레드 포인터(dangling thread pointer): 새로운 루트 노드를 만들어서 기존 이진 트리와 연결 가능. 기존 이진 트리의 루트 노드는 새롭게 생긴 노드의 왼쪽 서브 트리로 연결됨

스레디드 이진 트리의 중위 순회

• 스택 X, 스레드 포인터를 통해 이동 가능 → rightThread가 참이라면 중위 순회의 successor는 우측 자식. 그렇지 않다면 노드에 연결된 자식 노드의 좌측 자식을 향해 leftThread가 참일 때까지 탐색.

스레디드 이진 트리의 노드 삽입

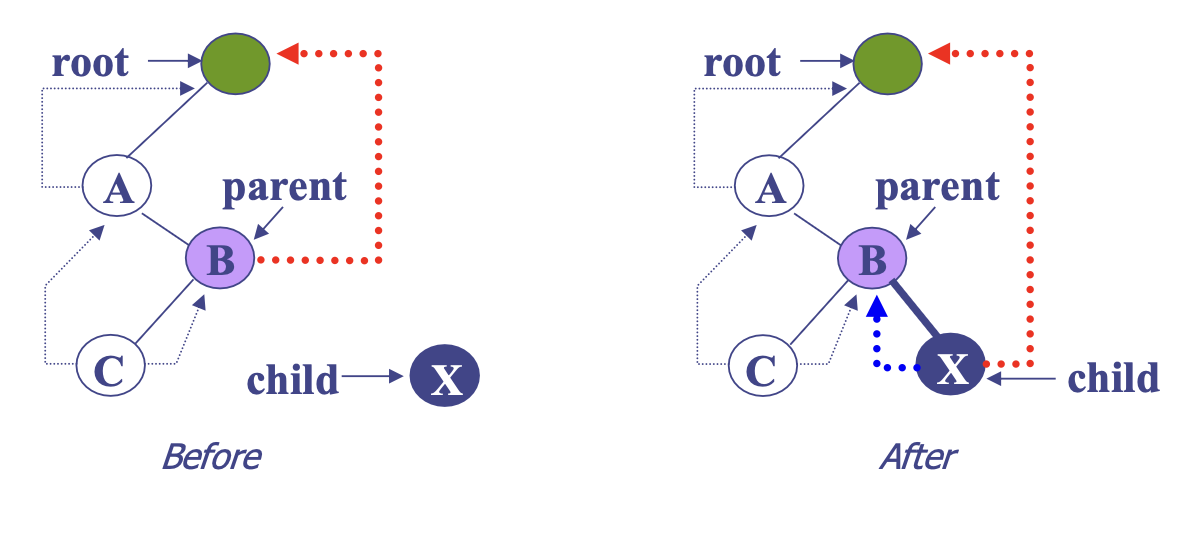
• 노드 X를 노드 B의 우측 자식을 삽입하기
• B의 우측 서브트리가 비었다면 곧바로 삽입
• B의 우측 서브트리가 있다면 X가 삽입된 이후 기존에 존재하던 B의 우측 서브트리를 X가 연결해야 함
  

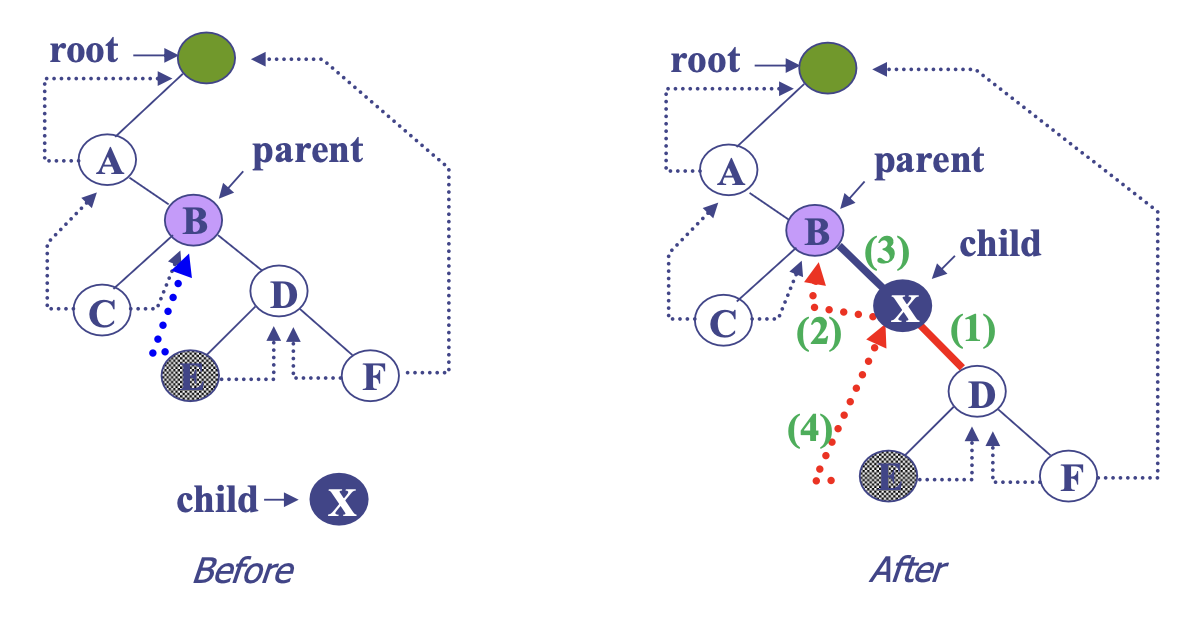
1. 삽입할 노드 X와 기존 노드 B의 우측 서브 트리의 루트 노드인 D를 연결(X의 우측 서브 트리 링크가 D를 잇기)
2. X의 좌측 스레드 포인터를 B로 연결하기
3. B의 우측 링크를 X로 연결
4. D의 좌측 서브 트리의 루트 노드인 E의 좌측 스레드 포인터를 X로 연결하기(중위 순회 순서가 변경되었기 때문)

Priority Queue

• 우선순위 기준으로 원소가 정렬된 큐 자료구조
  

힙

우선순위 큐를 구현하기 위해서는 heap이라는 자료구조가 필요하다!

• 최대 트리: 각 노드의 키 값이 자식 노드의 키 값보다 큰 트리
• 최대 힙: 최대 트리이자 동시에 완전 이진 트리인 경우
• 최소 트리: 최대 트리의 최소 버전
• 최소 힙: 최소 트리이자 동시에 완전 이진 트리인 경우
  완전 이진 트리이기 때문에 배열을 통해 효율적으로 표현 가능

import Foundation

struct Heap<T> {
    var nodes = [T]()
    let sort: (T, T) -> Bool
    
    init(sort: @escaping(T, T) -> Bool) {
        self.sort = sort
    }
    
    var isEmpty: Bool {
        return nodes.isEmpty
    }
    
    var count: Int {
        return nodes.count
    }
    
    func peek() -> T? {
        return nodes.first
    }
    
    func leftChild(from parentIndex: Int) -> Int {
        return parentIndex * 2 + 1
    }
    
    func rightChild(from parentIndex: Int) -> Int {
        return parentIndex * 2 + 2
    }
    
    func parentIndex(from childIndex: Int) -> Int {
        return (childIndex - 1) / 2
    }
    
    mutating func push(_ element: T) {
        nodes.append(element)
        siftUp(from: count-1)
    }
    
    mutating func siftUp(from index: Int) {
        var child = index
        var parent = parentIndex(from: child)
        
        while child > 0 && sort(nodes[child], nodes[parent]) {
            nodes.swapAt(child, parent)
            child = parent
            parent = parentIndex(from: child)
        }
    }
    
    mutating func pop() -> T? {
        guard !isEmpty else { return nil }
        
        nodes.swapAt(0, count-1)
        defer {
            siftDown(from: 0)
        }
        return nodes.removeLast()
    }
    
    mutating func siftDown(from index: Int) {
        var parent = index
        while true {
            let left = leftChild(from: parent)
            let right = rightChild(from: parent)
            var candidate = parent
            if left < count && sort(nodes[left], nodes[candidate]) {
                candidate = left
            }
            if right < count && sort(nodes[right], nodes[candidate]) {
                candidate = right
            }
            if parent == candidate {
                return
            }
            nodes.swapAt(parent, candidate)
            parent = candidate
        }
    }
}

var minHeap = Heap<Int>(sort: <)
minHeap.push(1)
minHeap.push(10)
minHeap.push(100)
minHeap.push(5)
minHeap.push(4)
minHeap.push(3)
minHeap.push(2)
minHeap.push(20)

while !minHeap.isEmpty {
    guard let node = minHeap.pop() else { break }
    print(node, terminator: " ")
}
// 1 2 3 4 5 10 20 100

힙 삽입

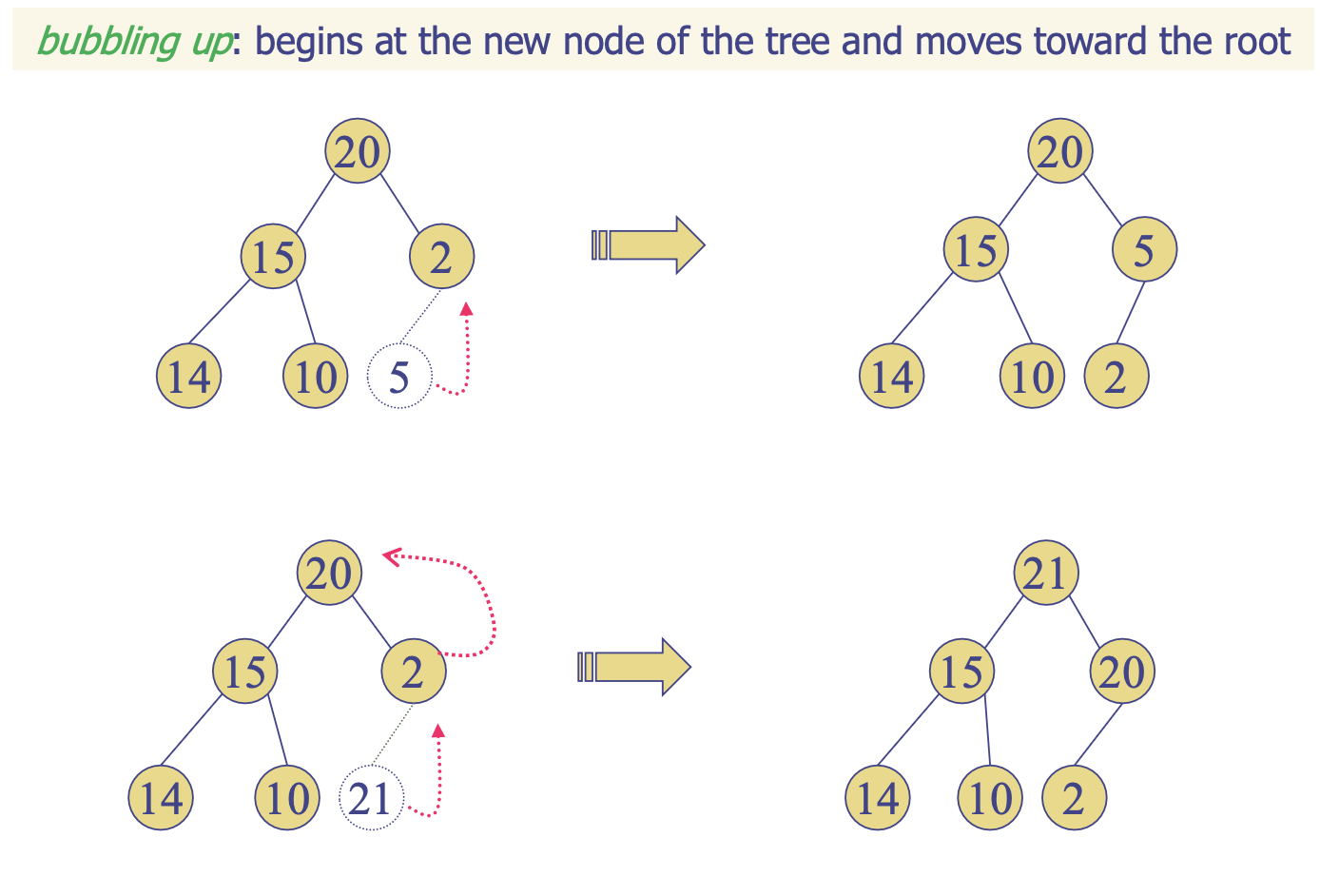
• 힙에 원소를 삽입했을 때 우선순위에 따라서 원소가 위치를 변경하는 과정

힙 삭제

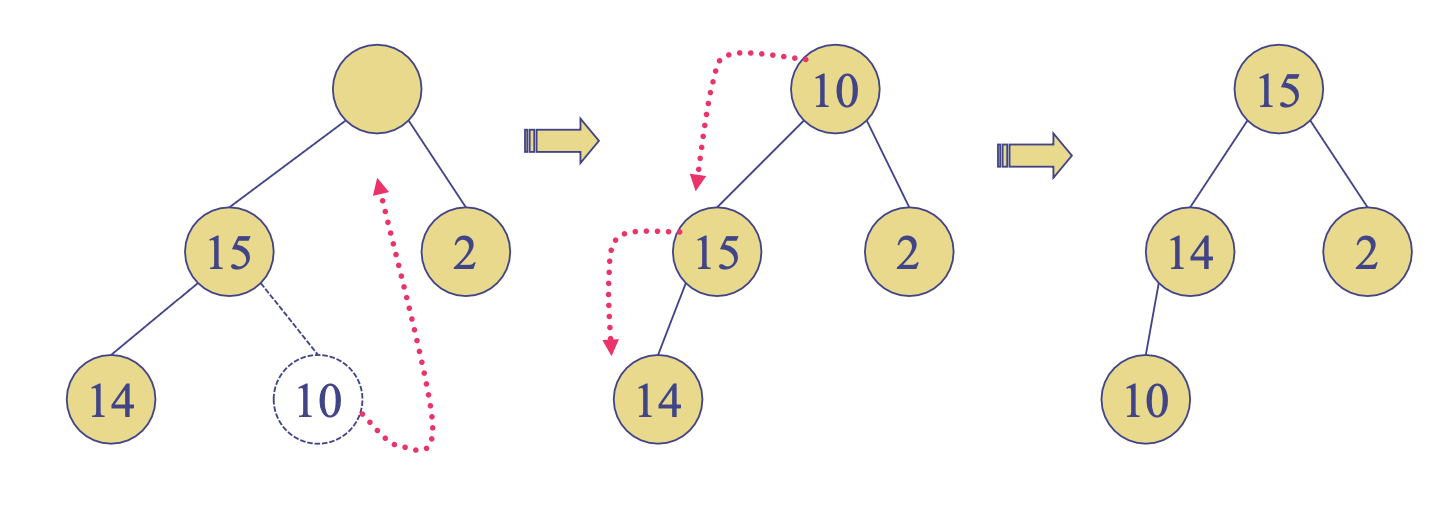
• 힙에 존재하는 원소를 삭제했을 때 우선순위에 따라서 원소가 위치를 변경하는 과정

이진 탐색 트리

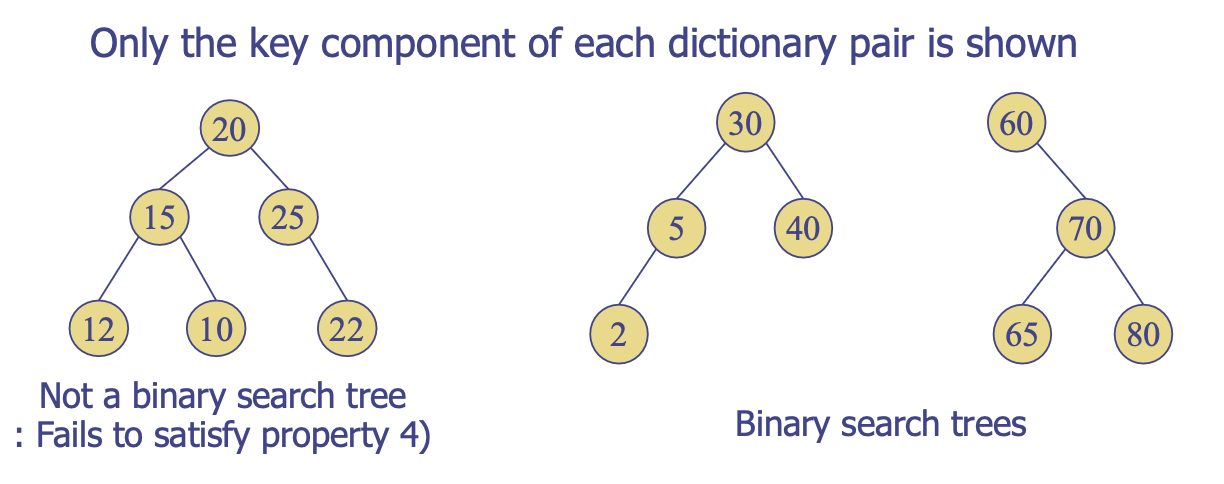
• 이진 트리이면서도 특정 조건을 만족하는 트리.
• 각 노드는 정확히 한 개의 키를 가지고 트리 안의 키들은 서로 다르다.
• 루트 노드의 키 값이 좌측 서브 트리보다 크다.
• 루트 노드의 키 값이 우측 서브 트리보다 작다.
• 좌측, 우측 서브 트리는 모두 이진 탐색 트리다. → 재귀적 정의

import Foundation

class Node<T> {
    var data:T
    var leftChild: Node?
    var rightChild: Node?
    
    init(data: T, leftChild: Node? = nil, rightChild: Node? = nil) {
        self.data = data
        self.leftChild = leftChild
        self.rightChild = rightChild
    }
}

struct BST<T> where T : Comparable {
    var root: Node<T>?
}

• 노드 오브젝트는 클래스로 선언, ARC 참조 카운팅 없을 경우 곧바로 메모리 할당 X
• 연결 리스트를 통해 이진 탐색 트리 구현 가능, 루트 노드를 옵셔널 노드 클래스로 선언

이진 탐색 트리 탐색

func searchIterative(_ element: T) -> T? {
        var root = self.root
        while root != nil {
            if root!.data == element {
                return element
            } else if root!.data > element {
                root = root!.leftChild
            } else {
                root = root!.rightChild
            }
        }
        return nil
    }
    
    func searchRecursive(_ root: Node<T>?, _ element: T) -> T? {
        if root != nil {
            if root!.data == element {
                return element
            } else if root!.data > element {
                return searchRecursive(root!.leftChild, element)
            } else {
                return searchRecursive(root!.rightChild, element)
            }
        }
        return nil
    }
    
    func inorderTraverse(_ root: Node<T>?) {
        if root != nil {
            inorderTraverse(root?.leftChild)
            print(root!.data)
            inorderTraverse(root?.rightChild)
        }
    }
    
    func preorderTraverse(_ root: Node<T>?) {
        if root != nil {
            print(root!.data)
            preorderTraverse(root?.leftChild)
            preorderTraverse(root?.rightChild)
        }
    }
    
    func postorderTraverse(_ root: Node<T>?) {
        if root != nil {
            postorderTraverse(root?.leftChild)
            postorderTraverse(root?.rightChild)
            print(root!.data)
        }
    }

• 이진 탐색 트리 내 특정 노드가 존재한다면 그 노드의 데이터를, 그렇지 않다면 nil을 리턴하는 탐색 함수를 반복 또는 재귀를 사용해 구현 가능
• 트리 자료 구조와 마찬가지로 순회 함수 모두 적용 가능

이진 탐색 트리 삽입

mutating func insert(_ element: T) {
        let node = Node(data: element)
        if let root = root {
            insert(root, node)
        } else {
            self.root = node
        }
    }
    
    func insert(_ root: Node<T>, _ node: Node<T>) {
        if root.data > node.data {
            if let leftChild = root.leftChild {
                insert(leftChild, node)
            } else {
                root.leftChild = node
            }
        } else {
            if let rightChild = root.rightChild {
                insert(rightChild, node)
            } else {
                root.rightChild = node
            }
        }
    }

• 최초의 삽입이라면 (현재 nil 값인) 루트 노드에 그대로 대입
• 루트 노드가 존재한다면 현재 루트의 데이터와 삽입된 원소의 값을 비교, 재귀 함수 호출 → 좌/우측 서브트리의 포인터 중 빈 노드를 삽입할 공간을 찾기

이진 탐색 트리 삭제

• 삭제할 노드가 존재할 때, 그 노드의 현재 상태를 확인한다. 즉 그 노드의 자식 개수가 몇 개인지(0, 1, 2)에 따라서 수행할 동작이 달라지기 때문이다.

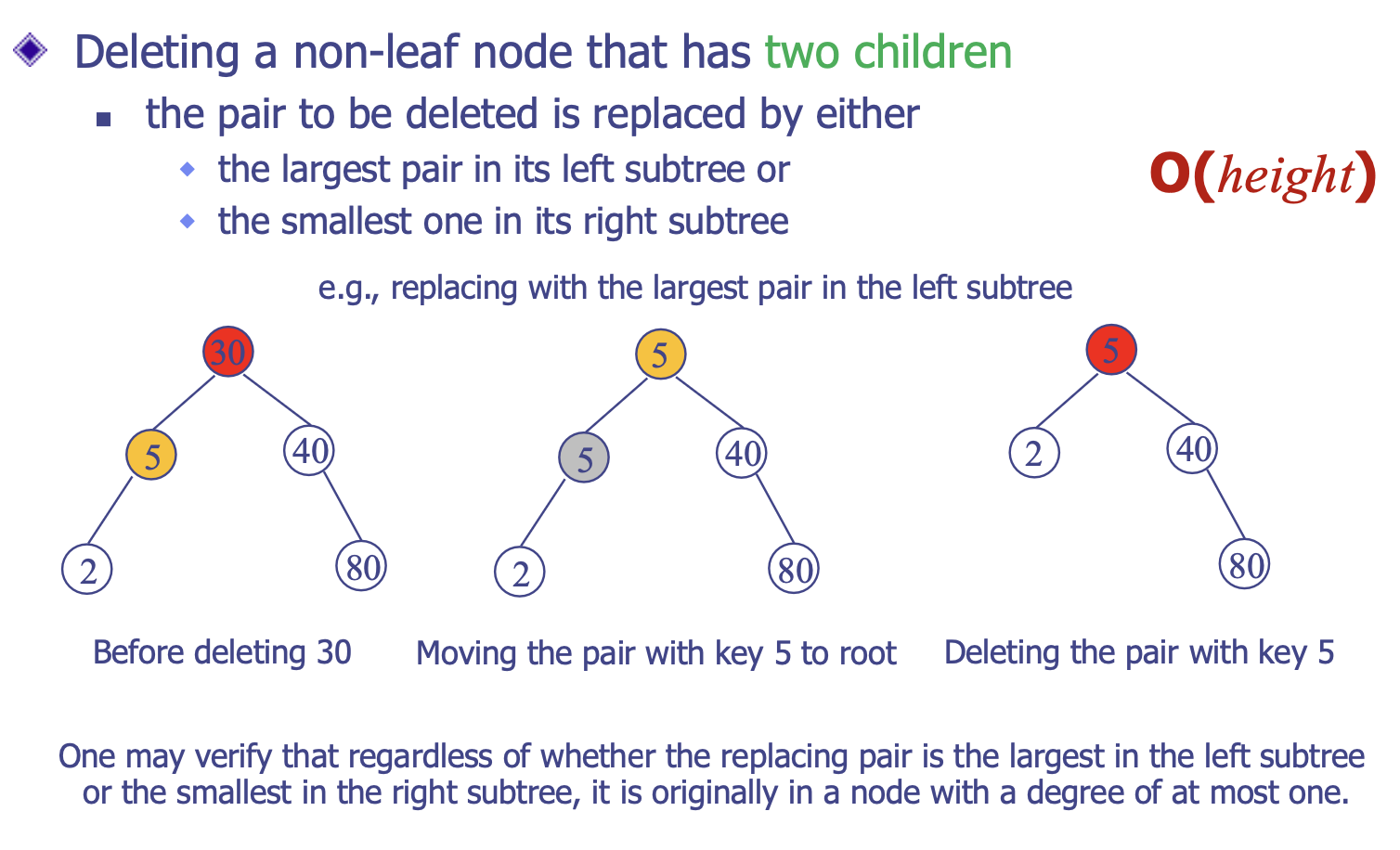
• 리프 노드 0개: 해당 노드와 그 노드의 부모 노드와의 가지 끊기
• 리프 노드 1개: 해당 노드의 자식과 해당 노드의 부모 노드와 연결시키기
• 리프 노드 2개: 해당 노드를 대체할 노드를 그 노드의 서브 트리에서 찾기(해당 구현에서는 삭제 노드의 우측 서브 트리의 leftmost한 노드를 대체 노드로 삼음) → 대체 노드는 최대 우측 서브 트리를 가지고 있는 리프가 1개인 노드이므로 위의 경우와 상동)

    
    mutating func delete(_ element: T) {
        root = delete(root, element)
    }
    
    func delete(_ root: Node<T>?, _ element: T) -> Node<T>? {
        guard let root = root else { return nil }
        
        if root.data == element {
            if root.leftChild == nil && root.rightChild == nil {
                return nil
            }
            if root.leftChild == nil {
                return root.rightChild
            }
            if root.rightChild == nil {
                return root.leftChild
            }
            if let leftmost = getLeftmost(root.rightChild) {
                root.data = leftmost.data
            }
            // min 값
            root.rightChild = delete(root.rightChild, root.data)
        } else if element < root.data {
            root.leftChild = delete(root.leftChild, element)
        } else {
            root.rightChild = delete(root.rightChild, element)
        }
        return root
    }
    
    func getLeftmost(_ root: Node<T>?) -> Node<T>? {
        var root = root
        while root?.leftChild != nil {
            root = root?.leftChild
        }
        return root
    }

이진 탐색 트리 병합 및 분할

• k 키 값을 기준으로 small, mid, big 세 가지로 구성 가능

선택 트리

• k개의 정렬된 시퀀스, runs가 하나의 정렬된 시퀀스로 병합되는 경우
• run: 여러 개의 레코드로 구성, key 데이터를 기준으로 오름차순 구성
• k 개의 runs 안에 각각 n개의 레코드 존재

Winner tree

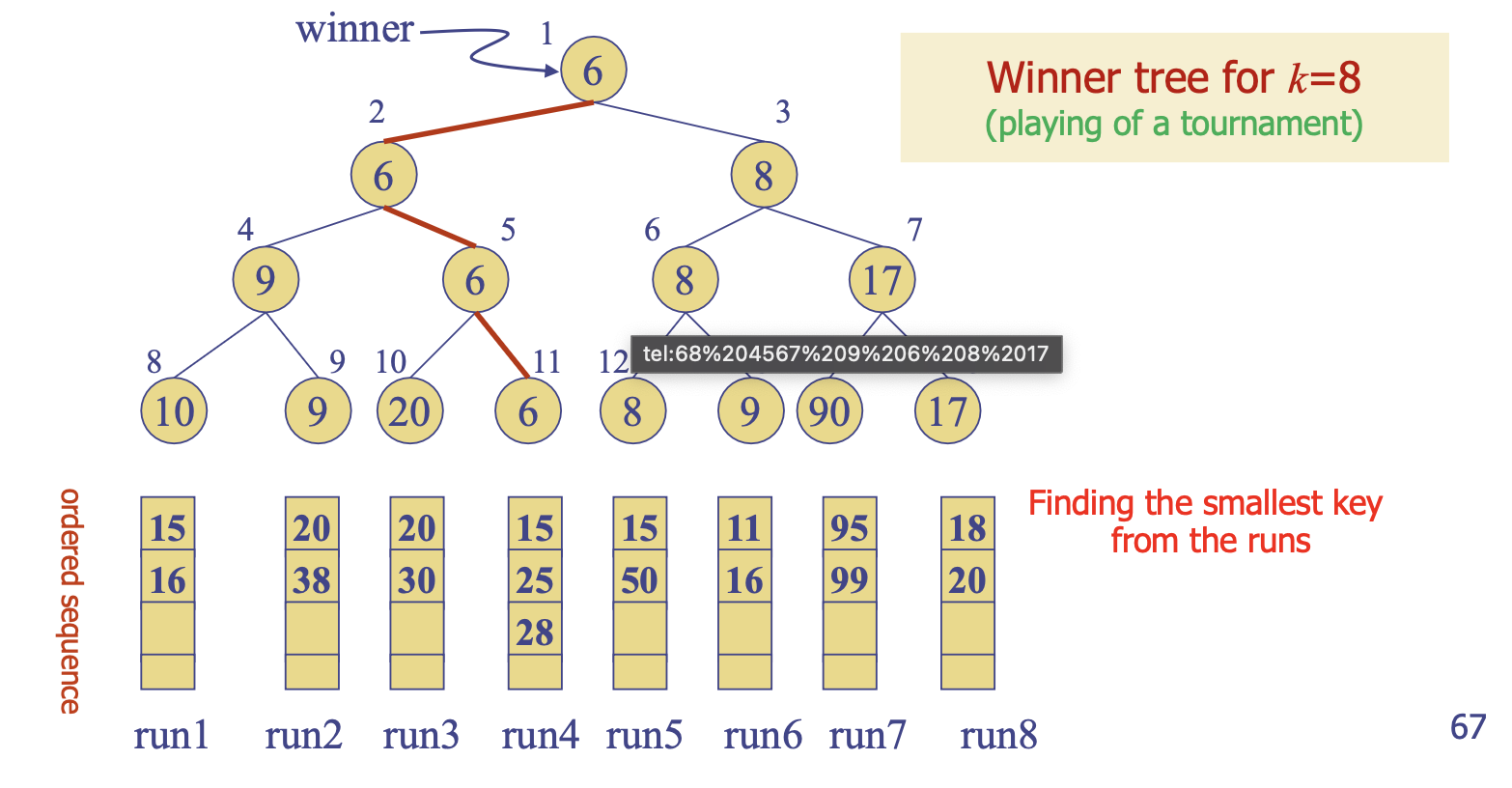
• 완전 이진 트리
• 각 노드는 두 자식 노드 중 더 작은 노드를 표현
• runs 큐에서 pop되는 노드들이 가장 하단부 8개 노드에 입력, 각각 비교를 통해 부모 노드의 값이 결정, 마지막 루트 노드 값이 정해질 때까지 결정됨
• 가장 작은/큰 값을 여러 개의 정렬된 시퀀스 큐에서 결정할 때 비교 횟수가 $O(log_2n)$으로 감소하는 효율적인 자료 구조

포레스트

• 서로 다른 트리들의 집합
  
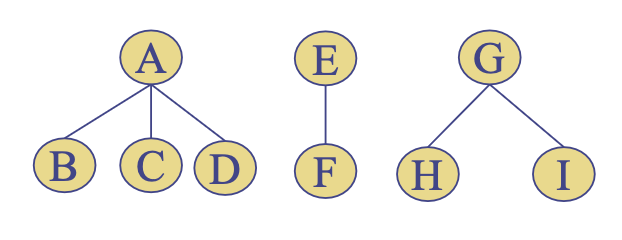
• 포레스트를 구성하는 서로 다른 트리들을 하나의 이진 트리로 만들기

1. $B(T_1, T_2..,T_n)$가 포레스트를 구성하는 각 트리 $T_n$.
2. 빈 포레스트일 때 $n=0$에는 이진 트리 구성 X
3. 루트 노드는 $T_1$의 루트 노드
4. 좌측 서브 트리는 $B(T_{11}, T_{12}, ..., T_{1m})$: $T_{nm}$은 $T_1$의 서브트리.
5. 우측 서브 트리는 포레스트를 구성하는 다른 트리들 $T_2, T_3,...,T_n$으로 구성 (재귀적)
   

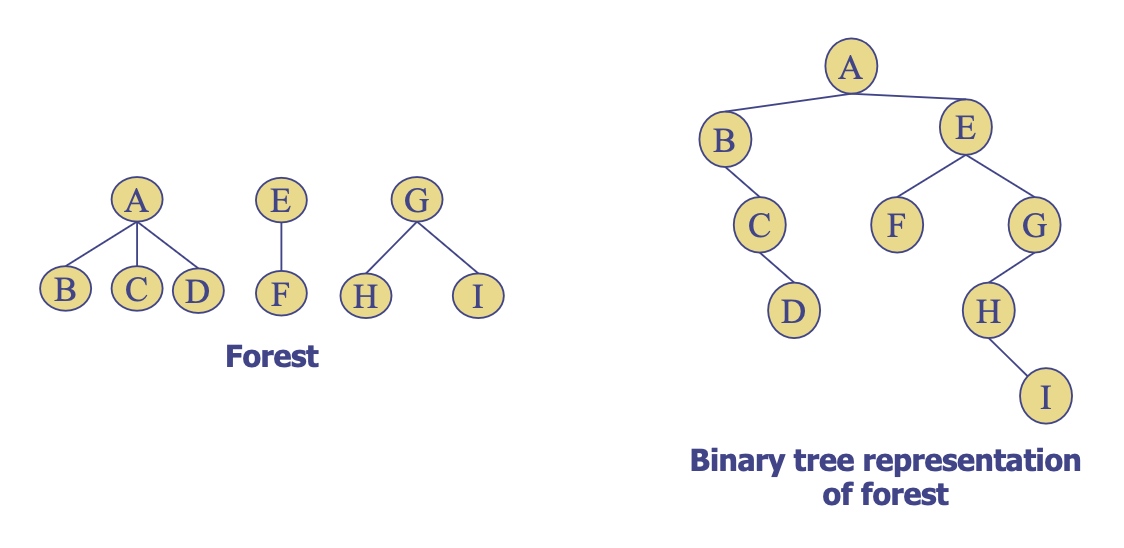
포레스트 순회

• $F$:포레스트
• Preorder: (1). $F$가 없다면 그대로 리턴 (2). $F$의 첫 번째 트리 $T$의 루트 노드 방문 (3). $T$의 서브 트리 순회하기 (4). $F$의 나머지 트리에 관해서 순회
• Inorder: (1). $F$가 없다면 그대로 리턴 (2). $F$의 첫 번째 서브 트리 순회 (3). 첫 번째 트리 $T$의 루트 노드 방문 (4). $F$의 나머지 트리에 관해서 순회

서로소 집합의 표현

• 트리 자료 구조를 통해 집합 표현 가능
• 두 트리 집합의 합집합 함수
• 특정 원소를 포함하는 트리를 리턴

트리를 통한 서로소 집합 표현

import Foundation

struct DisjointTree {
    private var nodes = Array(repeating: -1, count: 100)
    // 100개 사이즈 할당
    private var setPointers = Set<Int>()
    
    mutating func makeSet(setLabel: Int) {
        nodes[setLabel] = setLabel
        setPointers.insert(setLabel)
    }
    
    mutating func insertSet(setLabel: Int, elements: [Int]) {
        if setPointers.contains(setLabel) {
            for element in elements {
                nodes[element] = setLabel
            }
        }
    }
    
    mutating func unionSet(setLabel1: Int, setLabel2: Int) {
        if setPointers.contains(setLabel1) && setPointers.contains(setLabel2) {
            nodes[setLabel2] = setLabel1
        }
    }
    
    func getSet(setLabel: Int) {
        
        if setPointers.contains(setLabel) {
            for item in nodes.enumerated() {
                if item.element == setLabel {
                    print(item.offset, terminator: " ")
                    if item.offset != setLabel && setPointers.contains(item.offset) {
                        getSet(setLabel: item.offset)
                    }
                }
            }
        }
    }
}

var disjointTree = DisjointTree()
disjointTree.makeSet(setLabel: 1)
disjointTree.makeSet(setLabel: 2)
disjointTree.insertSet(setLabel: 1, elements: [3, 4, 5, 6, 7, 8])
disjointTree.insertSet(setLabel: 2, elements: [9, 11, 13, 15])
disjointTree.getSet(setLabel: 1)
// 1 3 4 5 6 7 8
disjointTree.getSet(setLabel: 2)
// 2 9 11 13 15
disjointTree.unionSet(setLabel1: 1, setLabel2: 2)
disjointTree.getSet(setLabel: 1)
// 1 2 9 11 13 15 3 4 5 6 7 8

• 배열을 통해 "가리키는" 포인터 및 데이터 표현
• 루트 노드는 곧 인덱스와 그 값이 상동한 원소
• 특정 집합에 포함된 노드는 집합 라벨을 값으로 가짐. E.g.) 원소 2가 1번 집합에 포함된다면 배열 2번 인덱스 값은 1로 설정