Hashing

• 딕셔너리의 탐색, 삽입, 삭제를 $O(1)$에 가능하게 하는 자료구조

Static Hashing

정적 해싱 소개

• hash table이라 불리는 테이블에 딕셔너리 쌍(키, 값)이 저장 → b개의 버킷으로 구분(ht[0], .., ht[b-1])
• 버킷: 개당 s 개의 슬롯을 가지고 있음. 각 슬롯은 하나의 딕셔너리 쌍을 가질 수 있을 정도로 충분한 크기
• hash function: 키가 k인 딕셔너리 쌍의 주소 공간을 결정하는 함수. 즉 키를 버킷에 매핑하는 함수 → 모든 키 k에 대해서 h(k) → 0 ~ b-1
• h(k)는 따라서 키 값 k의 주소 공간

정적 해싱의 정의

• Key Densitiy: 가능한 키의 개수 T 중 테이블에 존재하는 딕셔너리 (키, 값) 쌍의 개수 n이 어느 정도인지에 따라 결정. n/T
• Loading Density / Loading Factor: 버킷의 개수 b과 버킷이 개당 가지고 있는 슬롯의 개수 s를 곱하면 저장 가능한 총 공간이 나오는데, 이 총 공간에 현재 어느 정도로 딕셔너리 (키, 값) 쌍이 저장되어 있는지 보여줌. a=n/(sb)

해시 테이블

• 버킷의 개수는 일반적으로 가능한 키의 개수보다 적기 때문에 동일한 버킷에 여러 개의 키가 들어갈 수 있음
• 두 개의 키 $k_1$, $k_2$는 해시 함수 값이 같다면($h(k_1)==h(k_2)$) 서로 같은 synonym으로 판단
• overflow: 딕셔나리 (키, 값) 쌍을 이미 버킷이 가득 찬 곳에 삽입하려 할 때 발생
• collision: 새로운 딕셔너리 (키, 값) 쌍에 대한 버킷이 삽입하는 순간 비어 있지 않은 상태. 즉 다른 딕셔너리 쌍이 차지하고 있는 상태.

해시 함수

• overflow가 없다면 삽입, 삭제, 탐색은 현재 해시 테이블 상에 저장된 딕셔너리 (키, 값) 쌍의 개수 n과 상관없이 (1). 해시 함수 연산 시간 (2). 하나의 버킷을 탐색하는 시간 두 가지를 합한 시간 복잡도.
• 해시 함수로 인한 collsion이 최소화될 때 총 연산 비용 감소
• 동일한 해시 함수를 들어오는 모든 입력값에 사용

1. Division

• 가장 흔한 해시 함수
• 키 값이 음수가 아닌 경우 가정
• 버킷은 모듈러 연산(%)의 값을 담음
• $h(k)=k\%D$이기 때문에 버킷 인덱스는 (0...D-1)이고, 적어도 D개의 사이즈는 되어야 함
• D는 일반적으로 소수로 정하는데, (1). 작으면 홈 버킷의 분포도가 커지고 (2). 크다면 바이어스의 정도가 감소한다.

2. Mid-Square

• 주어진 키의 제곱근을 구하고 근삿값을 해시하는 함수

3. Folding

• 주어진 키 값 k가 여러 개의 부분으로 나눠지는데, 가능한 같은 크기로 나뉜다.
• E.g.) $k=12320324111220$으로 14비트. (3/3/3/3/2)의 다섯 부분으로 나뉠 수 있다. → $P_1=123, P_2=203,P_3=241,P_4=112,P_5=20$

1. Shift Folding: 마지막 부분을 제외한 다른 모든 부분들이 오른쪽으로 시프트 연산된다. 각 라인의 LSD(least significant digit)는 마지막 부분의 상응하는 디지트와 매칭. 다른 부분이 해시 함수를 구하기 위해 가산된다.
2. Folding at the boundaries: 분할이 이루어지는 경계 선상에 키가 나뉘고, 같은 곳으로 떨어지는 디지트가 해시 함수를 구하기 위해 서로 더해진다.

• Shift Folding → $h(k)=\sum^5_{i=1}P_i=123+203+241+112+20=699$
• Folding at the boundaries: folding의 경계는 $P_1$과 $P_2$, $P_3$과 $P_4$다. 각 두 번째 위치에 존재하는 파티션의 수를 거꾸로 한 뒤 가산한다. 즉 $h(k)=123+302+241+211+20=897$

4. Digit Analysis

• 사전에 주어진 모든 키 값을 알 수 있는 정적 파일에 유용한 방법
• 키 → 라딕스 r을 사용하는 수로 번역
• 라딕스를 통해 각 키의 디지트를 검사. 가장 휜 정도가 심한 디지트가 삭제됨
• 디지트 삭제가 충분히 이루어진다면 남아 있는 디지트는 주소 공간의 범위를 결정하는 데 많은 영향을 주지 않기 때문에 해시 함수로 기능

오버플로우 다루기

오픈 어드레싱

• 네 가지 방법 존재.

1. Linear Probing

• 키 값이 k인 딕셔너리 쌍을 삽입할 때 해시 테이블을 $ht[(h(k)+i)\%b], 0\leq i \leq b-1$ 순서대로 탐색
• 탐색 중 아직 딕셔너리 쌍이 없는 빈 버킷 공간을 발견하면 탐색 종료. 그 버킷에 삽입할 딕셔너리 쌍을 삽입한다.
• 빈 버킷이 없을 때(overflow): 테이블 사이즈를 늘려야 함
• loading density가 0.75 이상일 때 테이블 사이즈를 늘리는 게 해시 함수 비용에 이로움

  해시 테이블 사이즈를 늘리면 해시 함수 역시 새롭게 만들어야 한다!

import Foundation

struct CustomHash {
    
    private var dictionary: [String?]
    // bucket == slot == 1
    private var bucketSize:Int
    private let primeNumber = 13
    
    init(bucketSize: Int) {
        self.bucketSize = bucketSize
        dictionary = Array(repeating: nil, count: bucketSize)
    }

    private func getHashValue(_ key: String) -> Int {
        let asciiSum = key.map{Int($0.asciiValue ?? 0)}.reduce(0, +)
        return asciiSum % primeNumber
    }
    
    mutating private func makeDoubleDictionary() {
        let newDictionary:[String?] = Array(repeating: nil, count: bucketSize)
        bucketSize *= 2
        dictionary += newDictionary
    }
    
    mutating func insert(_ key: String) {
        let hashValue = getHashValue(key)
        
        for i in 0..<bucketSize {
            let validIdx = (hashValue + i) % bucketSize
            if dictionary[validIdx] == nil {
                dictionary[validIdx] = key
                return
            }
        }
        
        // overflow 발생 -> 해시 테이블 사이즈 2배로 늘리고 한 번더 insert 실행
        makeDoubleDictionary()
        insert(key)
    }
    
    func printDictionary() {
        for item in dictionary.enumerated() {
            if item.element != nil {
                print("Index \(item.offset) : \(item.element!)")
            }
        }
    }
}

var customHash = CustomHash(bucketSize: 5)
customHash.insert("dog")
customHash.insert("cat")
customHash.insert("tiger")
customHash.insert("lion")
customHash.printDictionary()
// Index 0 : cat
// Index 1 : tiger
// Index 2 : dog
// Index 3 : lion
customHash.insert("panda")
customHash.insert("horse")
customHash.insert("monkey")
customHash.insert("human")
customHash.insert("sheep")
customHash.printDictionary()
// Index 0 : cat
// Index 1 : tiger
// Index 2 : dog
// Index 3 : lion
// Index 4 : panda
// Index 5 : horse
// Index 6 : human
// Index 7 : sheep
// Index 9 : monkey

2. Quadratic Probing

• linear probing에서 i를 제곱하여 사용함
• $ht[h(k)+i^2]\%b, 0\leq i \leq b-1$

3. Rehashing

• 일련의 해시 함수를 계속해서 사용함

4. Random Probing

체이닝

• Linear Probing: 키 값 탐색이 다른 해시 값을 가지고 있는 딕셔너리 쌍과의 비교하기 때문에 효율적으로 좋지 않음
• 버킷 당 하나의 리스트가 있다면 해시 값을 리턴했을 때 곧바로 그 버킷에 주어진 키를 삽입할 수 있다. → 각 키스트가 모든 synonyms를 가지고 있음
• 해시 연산 시간: (1). 해시 주소 $h(k)$ 계산 (2). 해시 주소에 해당 키가 존재하는지 검사하는 시간

import Foundation

struct CustomChainingHash {
    private var dictionary: [[String]]
    private var bucketSize: Int
    private let primeNumber = 13
    
    init(bucketSize: Int) {
        self.bucketSize = bucketSize
        dictionary = Array(repeating: [String](), count: bucketSize)
    }
    
    private func getHashValue(_ key: String) -> Int {
        let asciiSum = key.map{Int($0.asciiValue ?? 0)}.reduce(0, +)
        return asciiSum % primeNumber
    }
    
    mutating func insert(_ key: String) {
        let hashValue = getHashValue(key)
        dictionary[hashValue % bucketSize].append(key)
        // 특정 키가 버킷 리스트 내에 존재한다 하더라도 탐색하지 않고 그대로 삽입 (중복 키 존재 가능)
        // 딕셔너리 버킷 아이템 내 키 존재 여부를 통해 결정 가능
    }
    
    func printDictionary() {
        for item in dictionary.enumerated() {
            if !item.element.isEmpty {
                print("Index \(item.offset) :", terminator: " ")
                for key in item.element {
                    print(key, terminator: " ")
                }
                print()
            }
        }
    }
}

var customChainHash = CustomChainingHash(bucketSize: 5)
customChainHash.insert("lion")
customChainHash.insert("tiger")
customChainHash.insert("whale")
customChainHash.insert("cat")
customChainHash.insert("cow")
customChainHash.printDictionary()
// Index 0 : lion cat
// Index 1 : tiger
// Index 4 : whale cow
customChainHash.insert("sheep")
customChainHash.insert("fish")
customChainHash.insert("human")
customChainHash.insert("monkey")
customChainHash.insert("ape")
customChainHash.insert("zibra")
customChainHash.insert("pig")
customChainHash.printDictionary()
// Index 0 : lion cat sheep fish
// Index 1 : tiger ape
// Index 3 : zibra pig
// Index 4 : whale cow human monkey

Dynamic Hashing

동적 해싱 소개

• 정적 해싱의 loading density → 스레드홀드 초과 시 해시 테이블의 사이즈를 변경 + 해시 함수 변경해야 하는 오버헤드 존재
• 동적 해싱: 재구축(rebuild)이 단 한 개의 버킷에서만 일어나도록 하는 해싱 기법. 즉 적절한 해시 테이블 퍼포먼스를 보장하는 방법
• $h(k, p)$: $h(k)$의 LSB $p$에 의해 만들어지는 정수

Directory

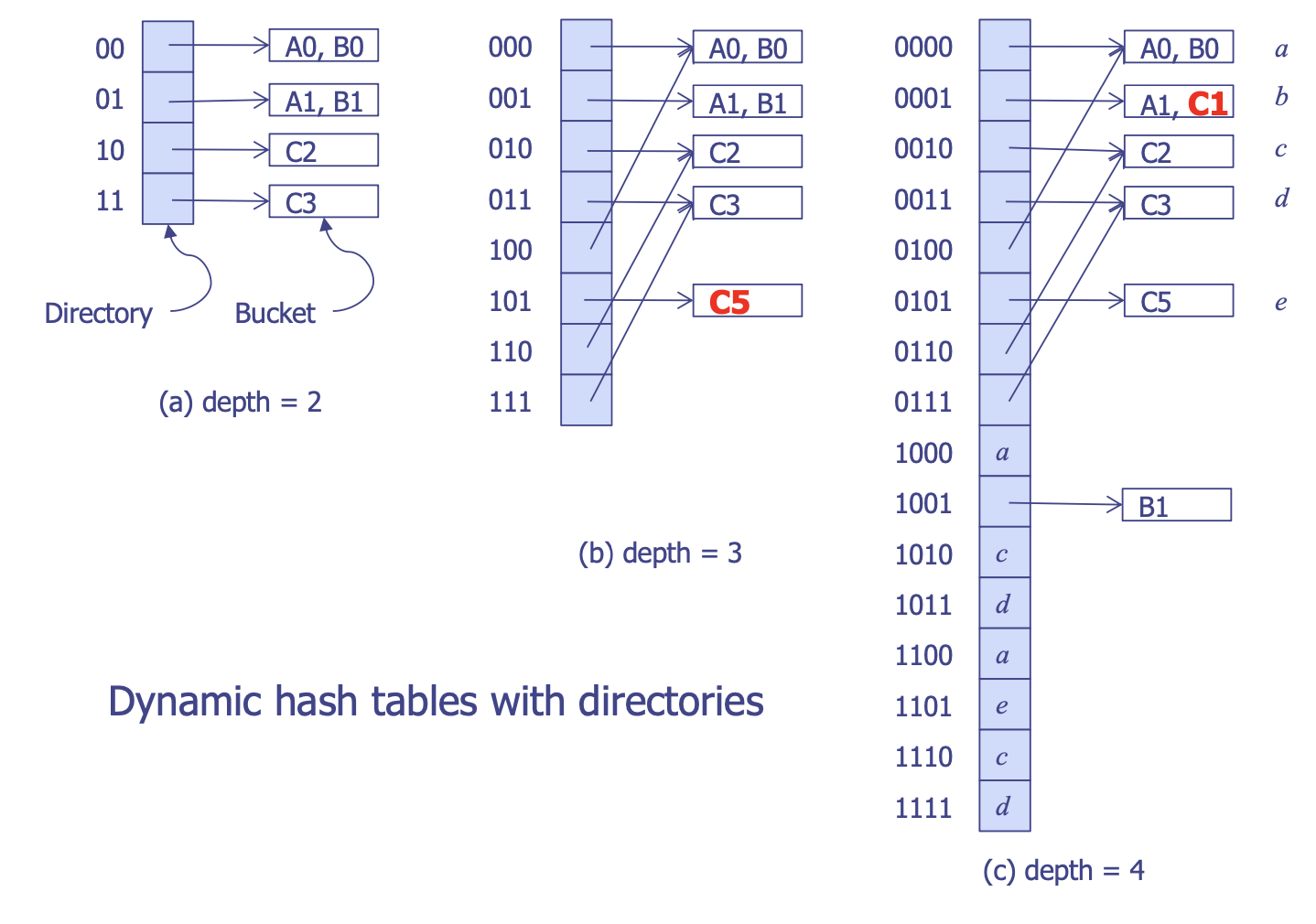
• 버킷 포인터에 대한 디렉토리 d 사용: 디렉토리 크기는 디렉토리 인덱스를 알아내기 위한 해시 함수 $h(k)$가 가지는 비트 개수에 따라 달라짐
• $h(k, n)$일 때 디렉토리 크기는 $2^n$으로 결정
• $h(k)$의 비트 개수는 디렉토리 패스(directory path)라고 불림
• 추가로 Directoryless 기법도 존재

import Foundation

struct DirectoryHash {
    private var directories = Array(repeating: [String](), count: 4)
    private var curDepth = 2
    private let bucketSize = 2
    
    private func getHashValue(_ key: String) -> Int {
        // 각 키의 비트 값은 사전에 미리 딕셔너리로 기록
        let hashDict = ["A0" : "100000", "A1" : "100001", "B0" : "101000", "B1" : "101001", "C1" : "110001", "C2" : "110010", "C3" : "110011", "C5" : "110101"]
        guard let bits = hashDict[key] else { return -1 }
        let bitsArray = Array(bits).map{String($0)}
        var LSBString = ""
        for idx in (bitsArray.count-curDepth+1)..<(bitsArray.count) {
            LSBString += bitsArray[idx]
        }
        guard let LSB = Int(LSBString) else { return -1 }
        return LSB
    }
    
    mutating func insert(_ key: String) {
        let hashValue = getHashValue(key) % directories.count
        
        if hashValue == -1 {
            return
        }
        
        if directories[hashValue].count < bucketSize {
            directories[hashValue].append(key)
        } else {
            let newDepthDirectories = Array(repeating: [String](), count: Int(pow(2.0, Double(curDepth))))
            directories += newDepthDirectories
            curDepth += 1
            relocate(hashValue)
            insert(key)
        }
    }
    
    mutating func relocate(_ hashValue: Int) {
        var removedKeys = [String]()
        for key in directories[hashValue] {
            let newHashValue = getHashValue(key)
            if newHashValue != hashValue {
                removedKeys.append(key)
            }
        }
        for key in removedKeys {
            guard let removedIdx = directories[hashValue].firstIndex(of: key) else { continue }
            directories[hashValue].remove(at: removedIdx)
        }
        for key in removedKeys {
            insert(key)
        }
    }
    
    func printDirectories() {
        for directoryItem in directories.enumerated() {
            if !directoryItem.element.isEmpty {
                print("idx: \(directoryItem.offset)", terminator: " ")
                for item in directoryItem.element {
                    print(item, terminator: " ")
                }
                print()
            }
        }
    }
}

var directoryHash = DirectoryHash()
directoryHash.insert("A0")
directoryHash.insert("B0")
directoryHash.insert("A1")
directoryHash.insert("B1")
directoryHash.insert("C2")
directoryHash.insert("C3")
directoryHash.printDirectories()
// idx: 0 A0 B0
// idx: 1 A1 B1
// idx: 2 C2
// idx: 3 C3
directoryHash.insert("C5")
directoryHash.printDirectories()
// idx: 0 A0 B0
// idx: 1 A1 B1
// idx: 2 C2
// idx: 3 C3
// idx: 5 C5
directoryHash.insert("C1")
directoryHash.printDirectories()
// idx: 0 A0 B0
// idx: 1 A1 C1
// idx: 2 C2
// idx: 3 C3
// idx: 5 C5
// idx: 9 B1

• 특정 키값이 입력될 때 해당 LSB를 읽을 수 있도록 문자열 딕셔너리로 가볍게 구현, 딕셔너리 포인터가 가리키는 버킷 역시 최대 사이즈 2의 문자열 배열로 구현