
Priority Queue
- 우선순위 큐: 우선순위를 기준으로 원소를 정렬한 자료구조
Single-Ended PQ
- 최대 힙, 최소 힙을 통해 각각 구현 가능 → 정렬 기준에 대한 한 가지 종류의 우선순위 큐 반환.
end가 그 우선순위를 가장 만족하는 루트 노드를 가리킨다 - 우선순위 큐 메소드: (1). 우선순위 해당 원소 리턴 (2). 원소 삽입 (3). 우선순위 해당 원소 삭제
우선순위 큐를 사용한 자료구조
meldable single-ended pq: 두 개 이상의 우선순위 큐를 병합해 하나의 우선순위 큐로 만들어주는 자료구조 -leftist trees,binomial heaps- 특정 원소 삭제 및 우선순위 감소 가능한 우선순위 큐:
fibonacci heaps,pairing heaps
Double-Ended PQ
- 최소 우선순위 큐 + 최대 우선순위 큐를 하나의 자료 구조 안에서 표현
- 최소 우선순위 원소를 리턴하기
- 최대 우선순위 원소를 리턴하기
- 임의의 우선순위를 가진 원소를 삽입하기
- 최소 우선순위 원소를 삭제하기
- 최대 우선순위 원소를 삭제하기
네트워크 버퍼에 DEPQ가 사용될 수 있다! 우선순위를 가진 패킷을 해당 큐에 받는다고 하자. 가장 먼저 보내야 하는(=우선순위 최대) 패킷은 2번 연산으로, 패킷을 버퍼에 삽입할 때에는 3번 연산으로, 버퍼가 가득 찰 때에는 4번 연산으로 핸들링해야 한다!
Leftist Trees
meldable PQ을 사용하는 효율적인 트리 구조n: 병합될 두 우선순위 큐가 가지고 있는 모든 원소 개수- 연산 속도: 삽입과 삭제 모두 logarithmic, 해당 우선순위 원소를 찾는 비용은 에 가능
힙을 사용할 때 병합은 이 걸린다!
Lefitst Trees의 정의
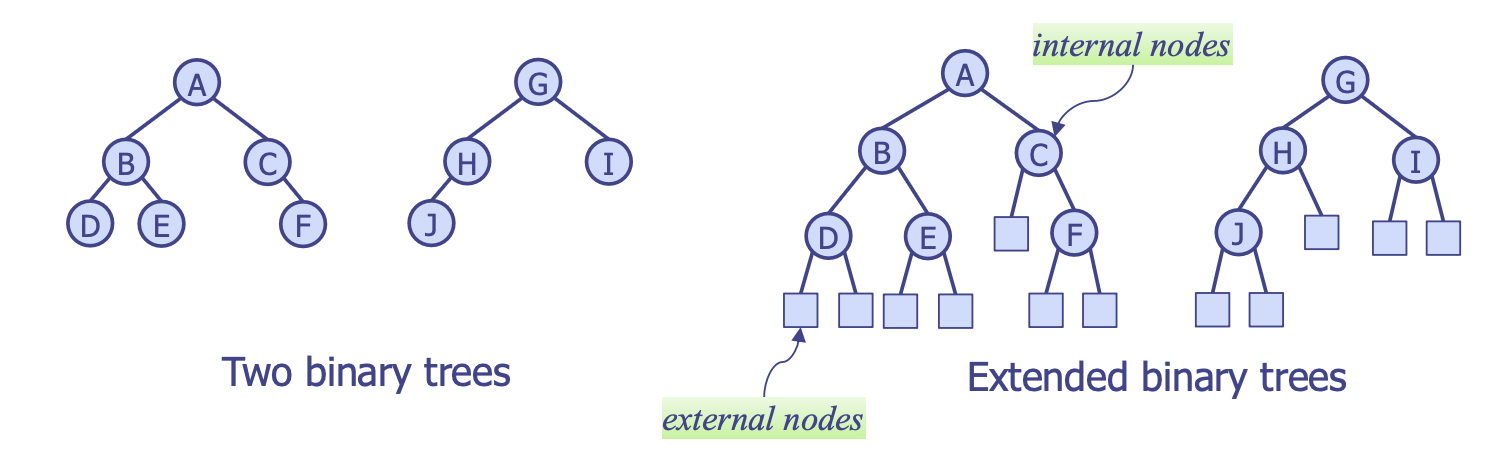
- 확장된 이진 트리(
extended binary tree) 채용 →internal nodes,external nodes두 가지 종류 - 존재하지 않는 노드라 할지라도 전체 모든 노드(
internal nodes)가 자식 노드 두 개를 가질 수 있도록 함
Height-Biased Leftist Trees
- 확장된 이진 트리의 노드
x: (1).leftChild(x)(2).rightChild(x)(3).shortest(x): 노드x에서 출발, 다른external node로 가는 가장 짧은 경로의 길이
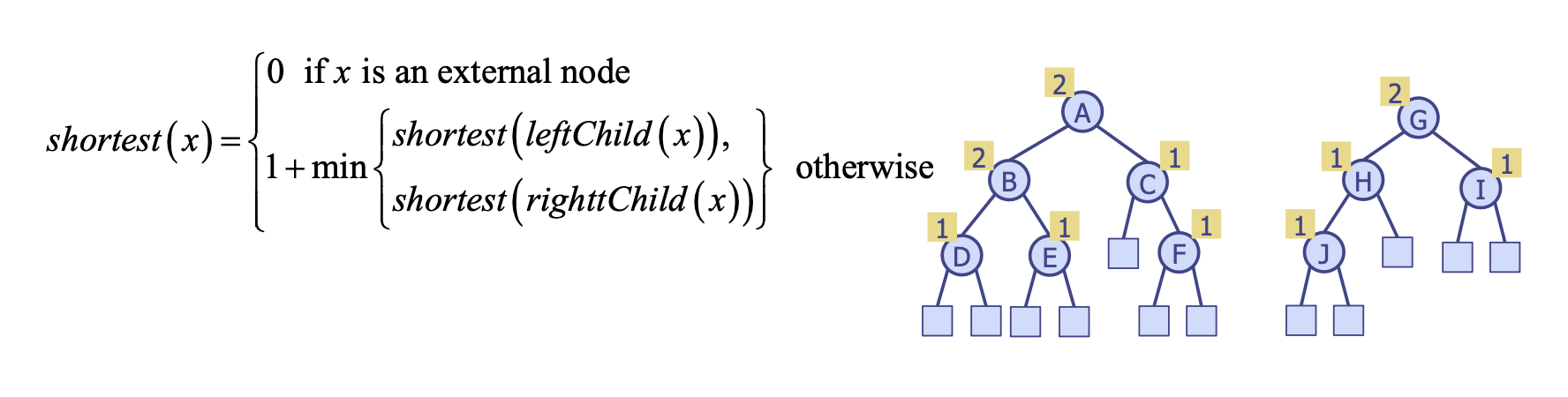
shortest계산: (1).external이라면 0 리턴 (2).internal이라면 두 자식 노드의shortest중 최솟값 + 1 리턴(재귀적 정의)leftist trees는 (존재한다면) 왼쪽 자식 노드의shortest가 우측 자식의shortest보다 언제나 같거나 크다.internal노드n개를 가지고 있는leftist tree의 루트 노드r이 있을 때 이고 루트 노드에서 가장 오른쪽에 치우쳐 있는external노드 경로는shortest(r)의 정의에 따르면 첫 번째 레벨에서는external노드가 없다. 즉 적어도 개의internal노드를 가진다.
Min Leftist Trees
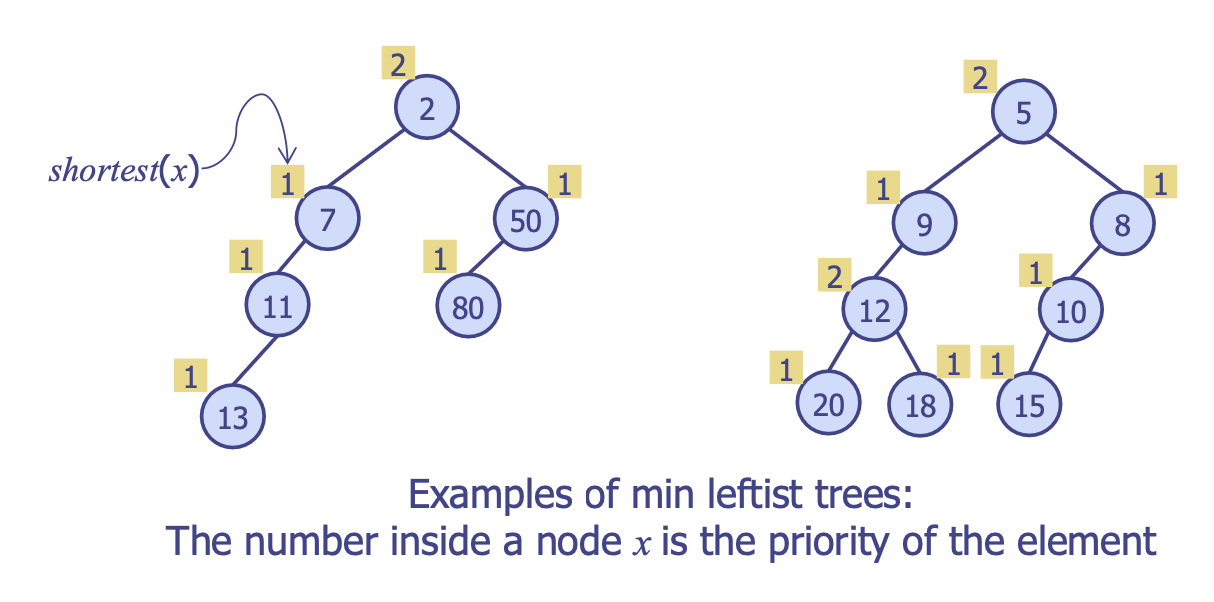
- 각 노드의 키 값이 자식 노드의 키 값보다 우선순위 정렬에 따르는 자료구조
- 최소/최대
leftist trees는 각각 일종의 최소/최대 트리 - 병합 연산을 통해 삽입 및 삭제 연산 가능
- 최소
leftist tree에 원소x를 삽입할 때: (1). 하나의 원소x만 가지고 있는 최소leftist tree를 만들기 (20. 두 최소leftist trees를 병합하기 - 최소
leftist tress에서 최솟값을 삭제할 때: 루트 노드의 우측 서브 트리와 좌측 서브 트리를 병합하고 기존 루트 노드는 리턴
Min Leftist Tree의 병합 연산
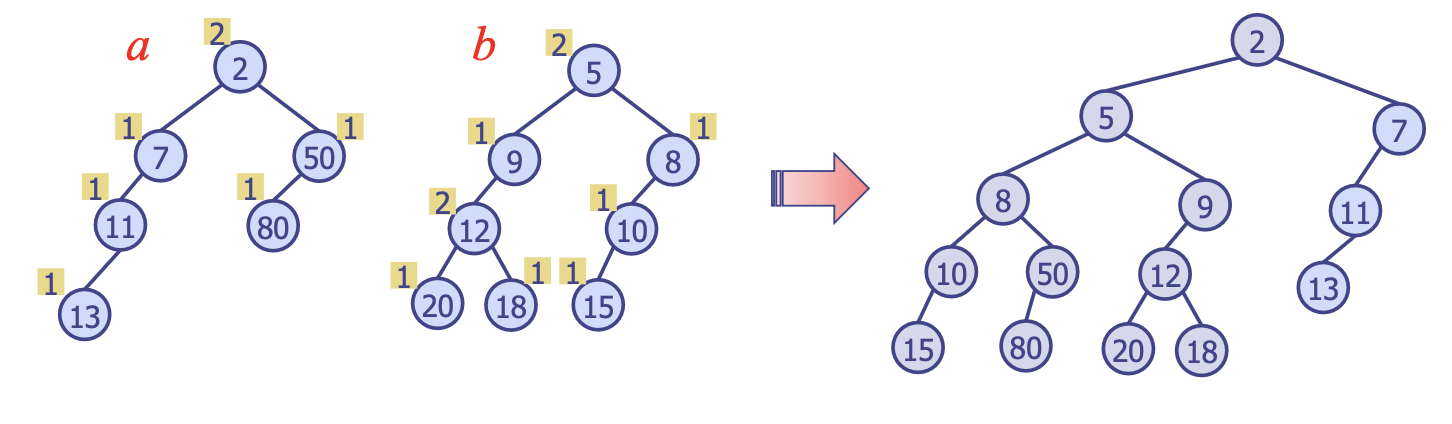
- 병합할 두 이진 트리의 원소를
rightmost경로를 따라 모으면서 이진 트리 만들기 - 해당 이진 트리를
leftist tree로 만들기 위해 필요한 만큼 좌측, 우측 서브 트리를 바꾸기
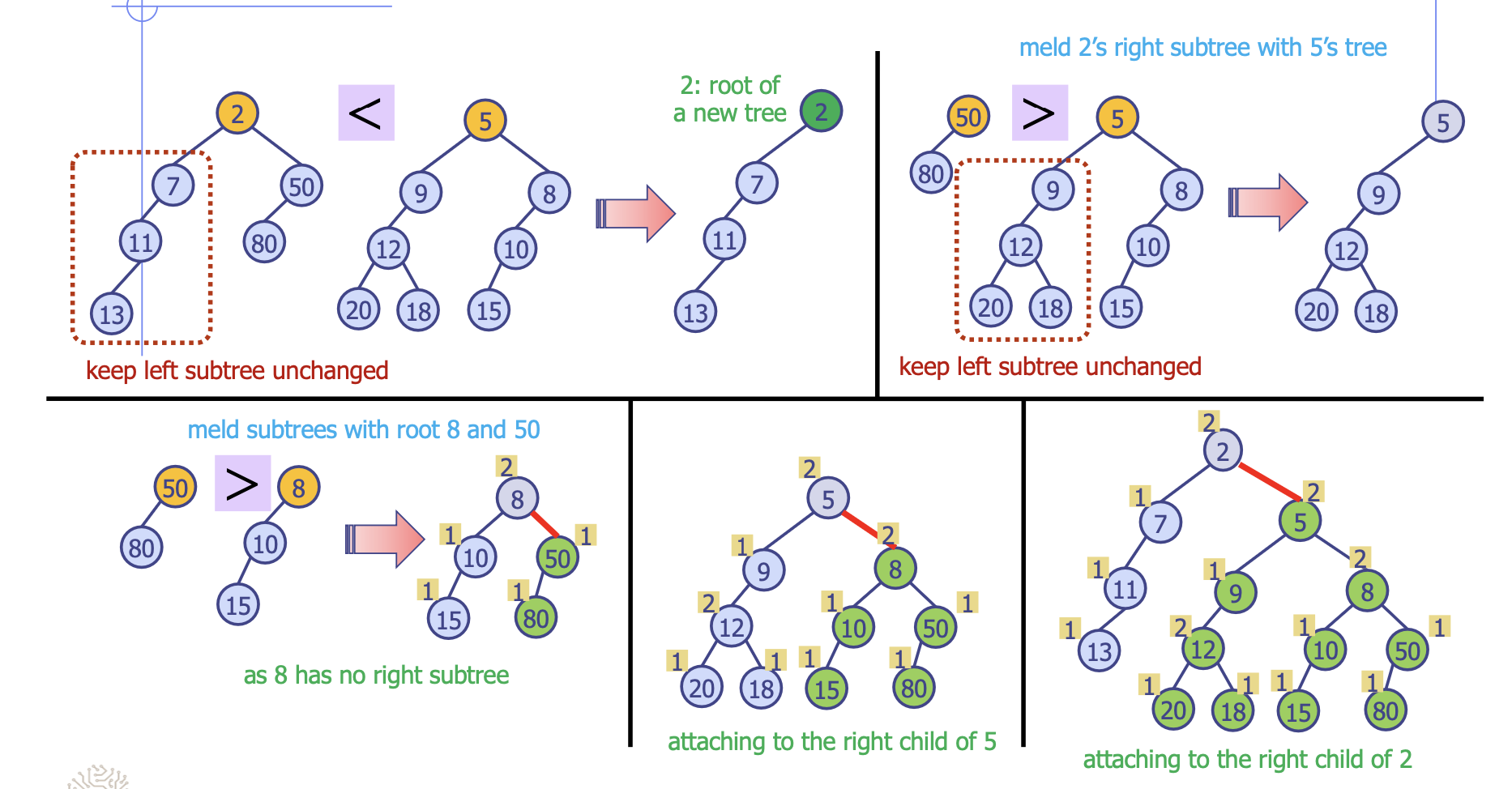
- 재귀적으로
leftists tree의 왼쪽부터 붙을 브런치를 교환하면서 만들어가기
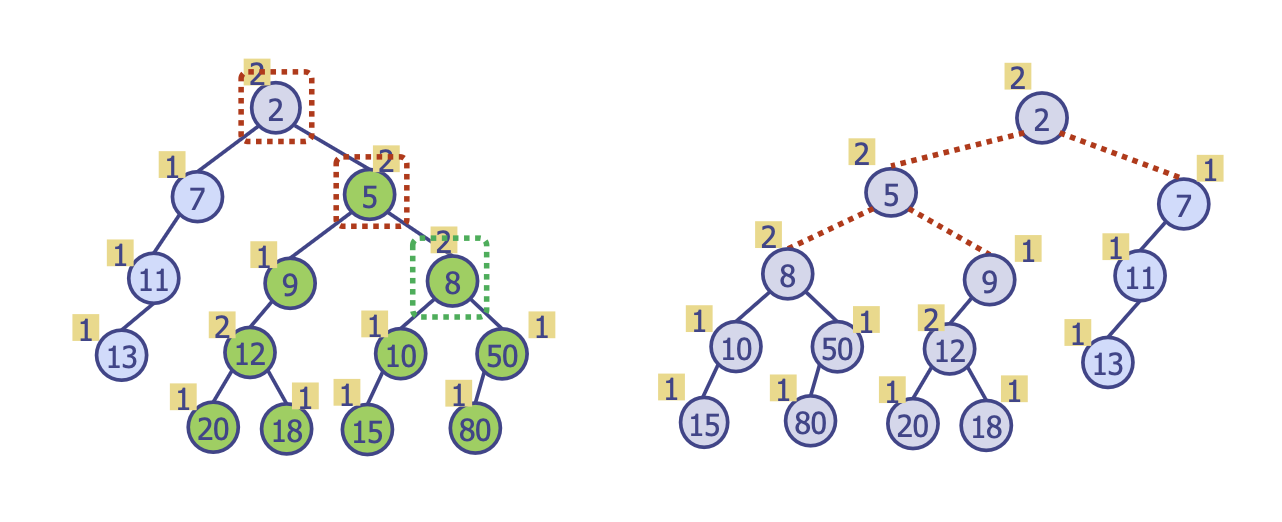
leftist tree를 한 번 구성한 뒤에는 필요 조건인shortest의 경로 길이가 좌측 서브 트리가 우측 서브 트리보다 같거나 커야 한다는 점을 만족할 수 있도록 계속해서 교환하자!
Weight-Biased Leftist Trees
HBLT처럼 트리 내external노드까지의 경로 길이가 아니라 트리를 구성하는 노드의 개수를 고려하는 자료 구조- 특정한 노드
x의 가중치인 는 루트 노드x및 서브트리의internal노드 개수다.
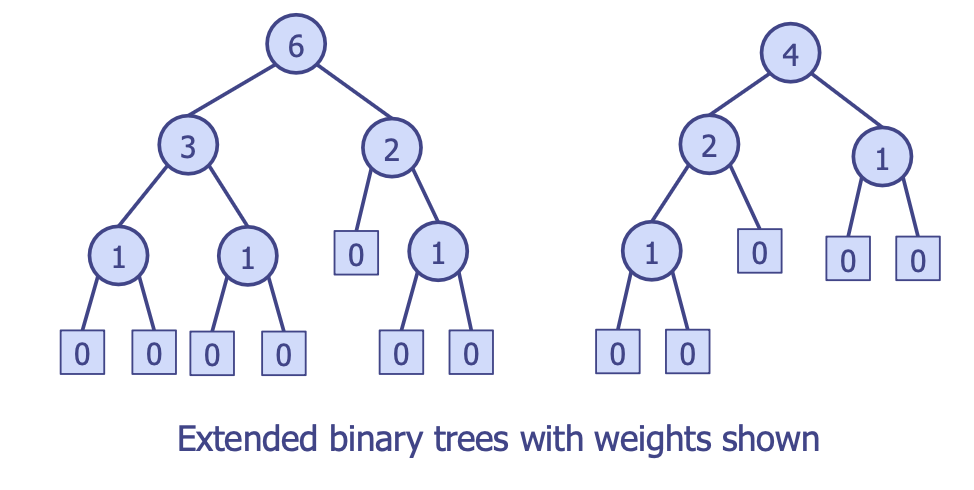
extenral노드일 때에는 가중치 값은 0internal노드일 때에는 자식 노드의 가중치를 합한 데 + 1을 리턴external노드의 가중치 값이 0이기 때문에 리프 노드부터 계산, 루트 노드까지 가중치 값을 계산하는 게 보다 편리하다!- 모든
internal노드에서 좌측 자칙의 가중치 값이 우측 자식 가중치 값 이상이라면WBLT로 간주할 수 있다.최대, 최소
WBLT는 곧WBLT인 최대, 최소 트리이다! WBLT의 특정 노드x는 해당 노드에서 가장 우측에 있는(rightmost)까지의 길이가 을 만족한다.
Binomial Heaps
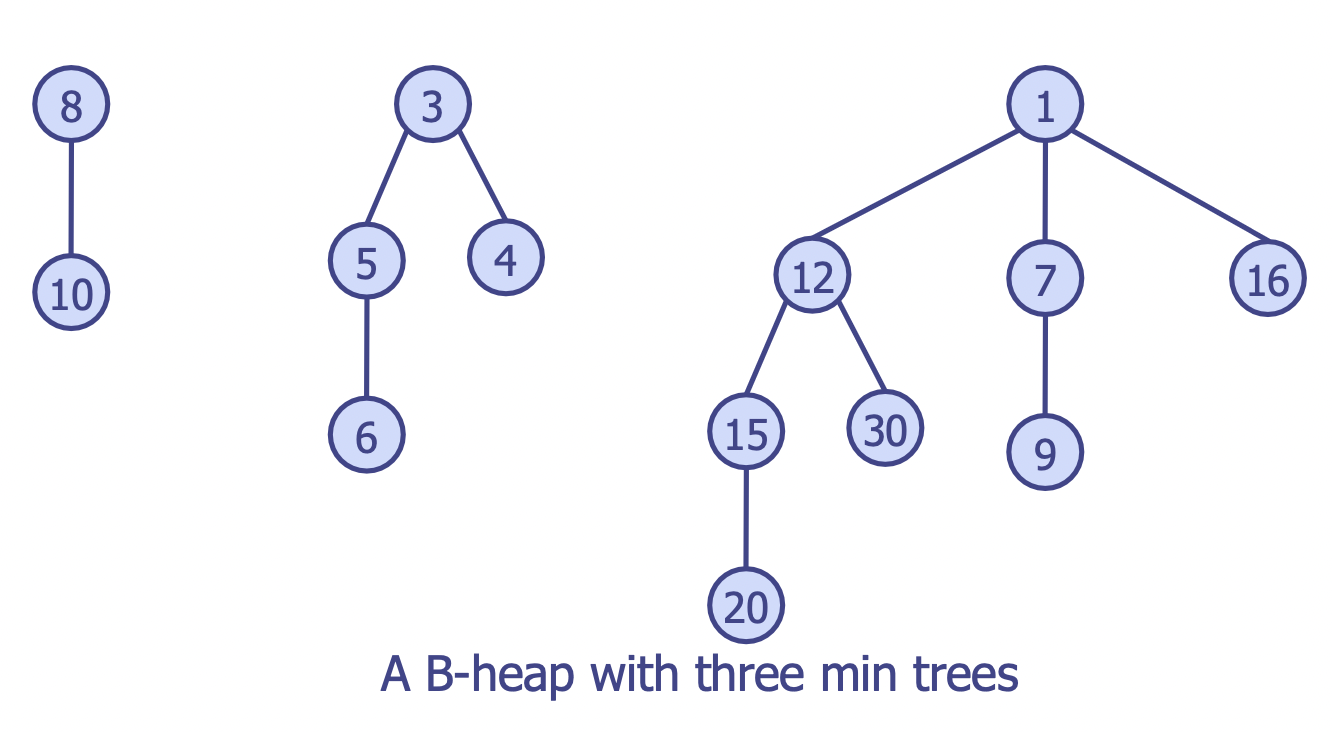
Leftist trees에서 지원 가능한 모든 함수 가능- 삽입, 삭제, 병합 등 개별 연산이 에 가능한
leftist trees에 비해 특정 상황에서는 이 걸릴 수도 있음 → 비용이 큰 연산을 비용이 작은 연산에amortize할 때 시간 복잡도를 또는 에 할 수 있음. - (1). 최소 트리의 집합 - 최소 이진 힙 (2). 최대 트리의 집합 - 최대 이진 힙
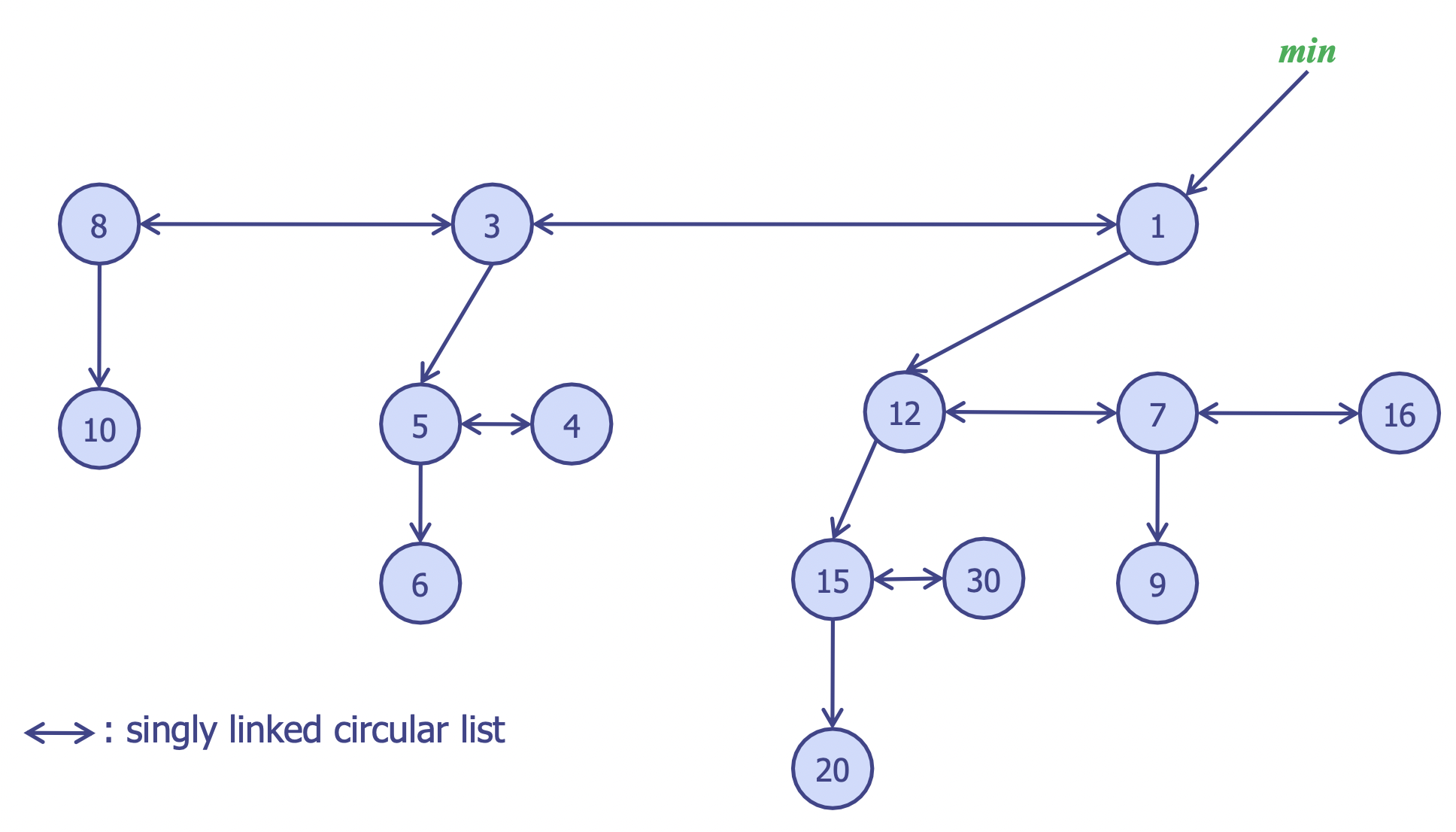
- 이진 힙 노드: (1). degree: 자식의 개수 (2). child: 자식 노드에 대한 포인터 (3). link: sibling과 단일 연결 원형 리스트로 구성 (4). data
- 노드의 모든 자식: 단일 연결 원형 리스트로 구성 및 포인터
- 최소 트리의 루트: 단일 연결 원형 리스트로 링크
- 가장 키 값이 작은 최소 트리의 루트 노드에 대한 단일 포인터
min이 해당 이진 힙을 포인터로 가리키고 있음
Insertion
- 원소
x노드 삽입 min이 가리키고 있는 원형 리스트에 해당 노드 삽입min이 0이거나 해당 노드x의 키 값이 더 작을 때에만min값이 새로 갱신됨- 시간 복잡도
Melding
- 두 개의 존재하는(
non-empty) 이진 힙을 병합 - 최상단 원형 리스트를 단일 원형 리스트로 병합
- 새로운 이진 힙 포인터는 두 트리 중 최솟값의
min포인터 - 두 원형 리스트를 하나의 원형 리스트로 병합하는 데
constant이기 때문에 결과적으로 병합 연산 또한
Deletion
- 이진 힙의
min이 가리키는 값을 리턴한 뒤 생기는 서로 다른 트리를 다시 이진 힙 상태(각 트리의degree가 서로 다른 상태)로 만드는 과정까지 포함
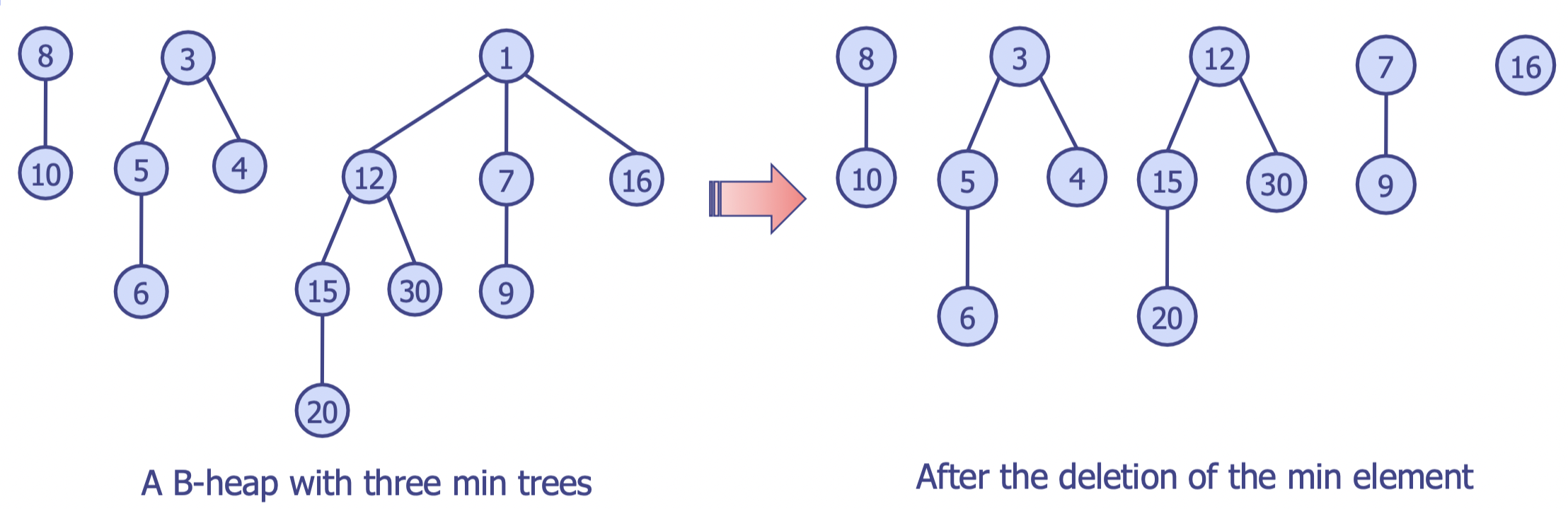
- 현재
min이 가리키고 있는 노드를 리턴, 해당 노드가 루트 노드인 이진 힙의 서브 트리를 분리
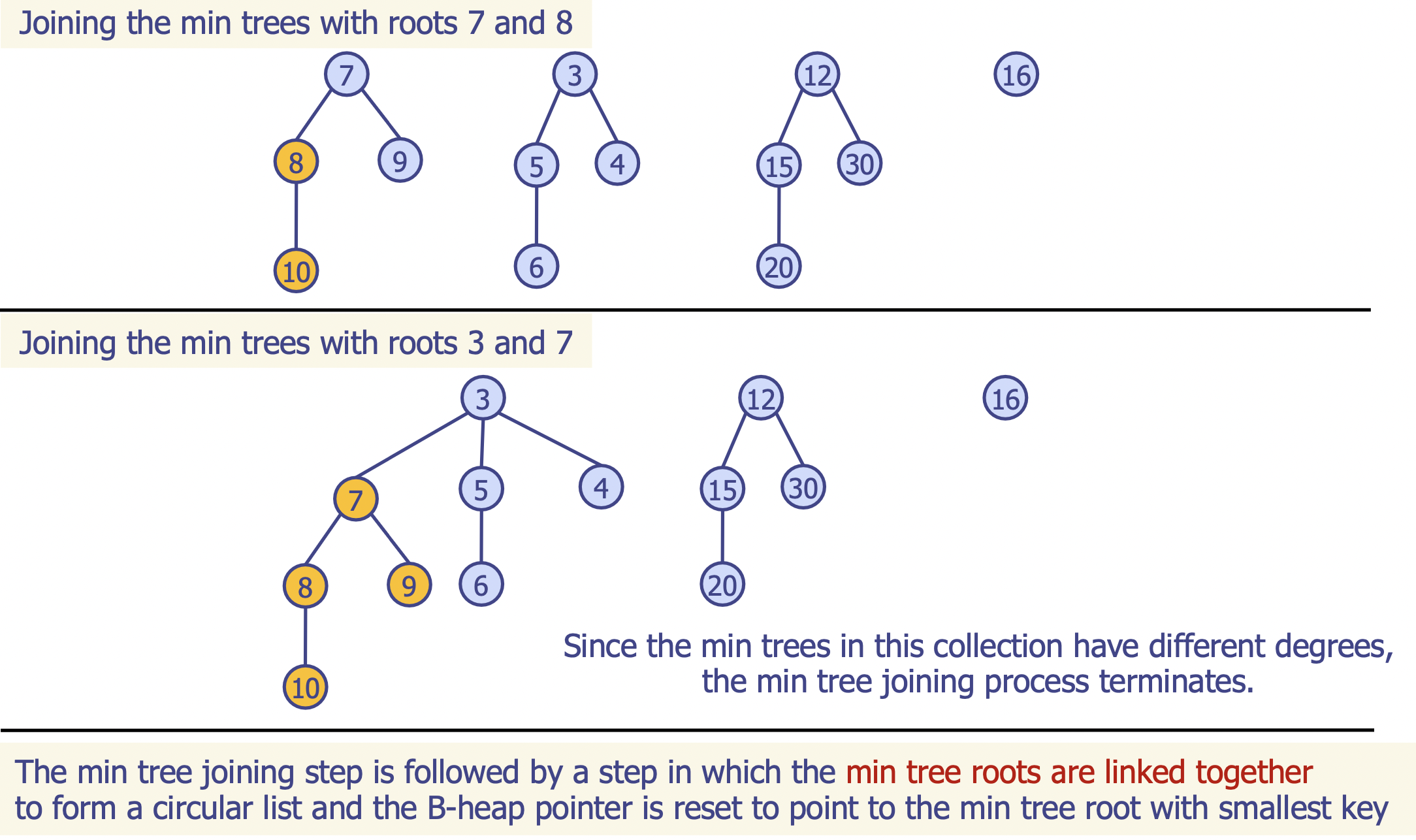
- 같은
degree를 가지고 있는 최소 트리 쌍을 조인 - 이진 힙의 정의(이진 힙 내 서로 다른 트리 루트 노드의
degree가 모두 다른 상태)를 만족할 때까지 반복
Fibonacci Heaps
- 이진 힙의 세 가지 연산(삽입, 최소/최대 삭제, 병합)과 별개의 연산 가능
- 임의의 원소 삭제
- 특정 노드의 키를 낮추기
- (1). 최소 트리의 집합 - 최소 피보나치 힙 (2). 최대 트리의 집합 - 최대 피보나치 힙
Deletion
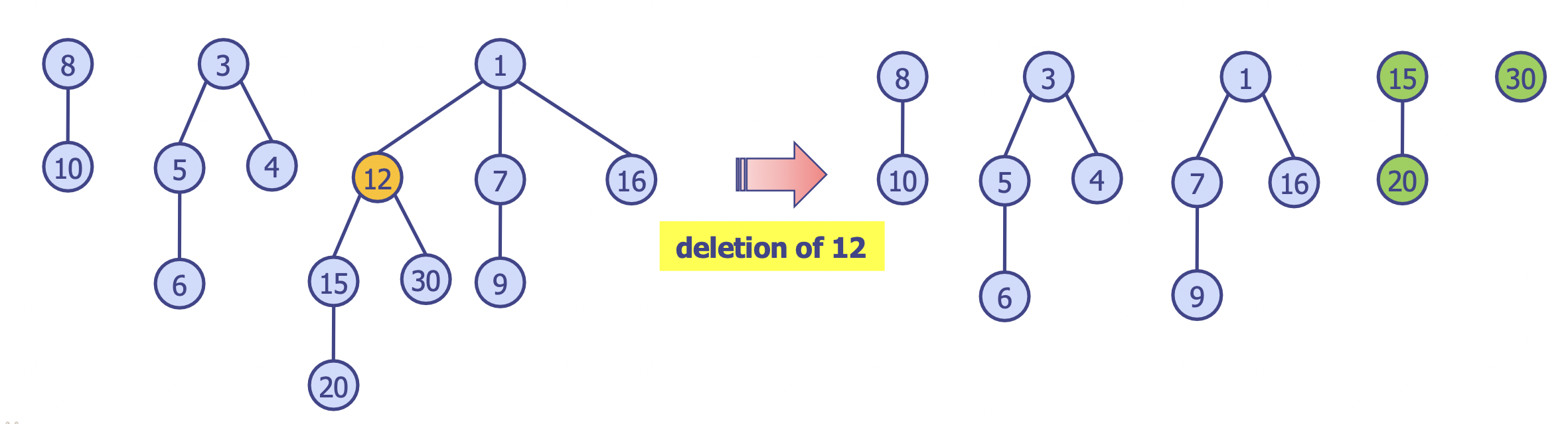
- 피보나치 힙을 구성하는 특정 힙
a에서 특정 노드b를 삭제하는 과정
a와b가 같다면delete min연산을 수행b노드가 들어 있는 이중 연결 리스트에서 해당 노드 삭제b의 서브 트리를b가 연결되어 있는 해당 트리에서 분리b를 리턴해당 노드를 분리해서 서브 트리 두 개가 더 만들어졌다 할지라도 이진 힙의 삭제처럼 트리를 조인하지는 않는다!
Decrease Key
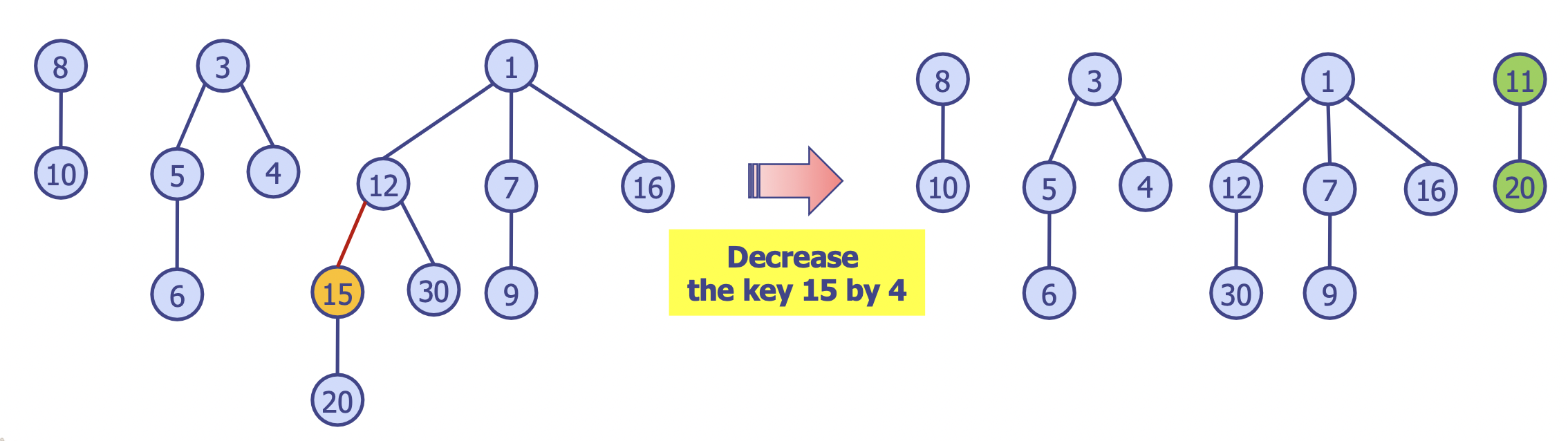
- 특정 노드
b의 키를 감소시키는 과정
b의 키를 감소시키기b가 최소 트리의 루트가 아니고 현재 키 값이 부모 노드보다 작다면b를 이중 연결 리스트에서 삭제, 최소 트리 루트의 이중 연결 리스트에 삽입- 최소 우선순위에 맞추어 포인터를 변경
