문제 설명
n개의 노드가 있는 그래프가 있습니다. 각 노드는 1부터 n까지 번호가 적혀있습니다. 1번 노드에서 가장 멀리 떨어진 노드의 갯수를 구하려고 합니다. 가장 멀리 떨어진 노드란 최단경로로 이동했을 때 간선의 개수가 가장 많은 노드들을 의미합니다.
노드의 개수 n, 간선에 대한 정보가 담긴 2차원 배열 vertex가 매개변수로 주어질 때, 1번 노드로부터 가장 멀리 떨어진 노드가 몇 개인지를 return 하도록 solution 함수를 작성해주세요.
제한사항
노드의 개수 n은 2 이상 20,000 이하입니다.
간선은 양방향이며 총 1개 이상 50,000개 이하의 간선이 있습니다.
vertex 배열 각 행 [a, b]는 a번 노드와 b번 노드 사이에 간선이 있다는 의미입니다.
문제 풀이
문제 이해 및 알고리즘 구상은 다소 간단한 편이다. 1에서 각각의 노드로 도착하는데 걸리는 최단 거리를 저장하고 순회가 끝나면 가장 높은 수를 찾아 그 수의 개수를 찾으면 되는 문제이다. 정리하자면,
- 2~n 까지 순회하며 1에서 올 수 있는 최단 거리 찾아서 저장.
- 거리의 집합 중 최대 값 찾음.
- 최대 값이 집합에 몇 개나 포함 된지 찾음.
이렇게 정리 할 수 있겠다. 그렇다면 최단 거리를 구하는 방법만 안다면 쉽게 풀 수 있을 것이다. 최단거리나 그래프 문제는 c++을 사용하는게 뭔가 좀더 생각하기 편해서 주로 c++을 자주 사용한다.
문제 자체는 쉽지만 최단 거리 알고리즘 자체가 아주 중요하기 때문에 이번 문제를 계기로 한번 정리 해보도록 하겠다.
최단 거리 알고리즘
최단 거리 알고리즘의 경우 크게
- BFS
- 다익스트라 알고리즘
- 벨만-코드 알고리즘
- 플로이드 워쉘 알고리즘
이렇게 4가지로 나눌 수 있다. 사용 상황에 대해 표로 정리하자면 아래와 같은 표로 표현할 수 있다.
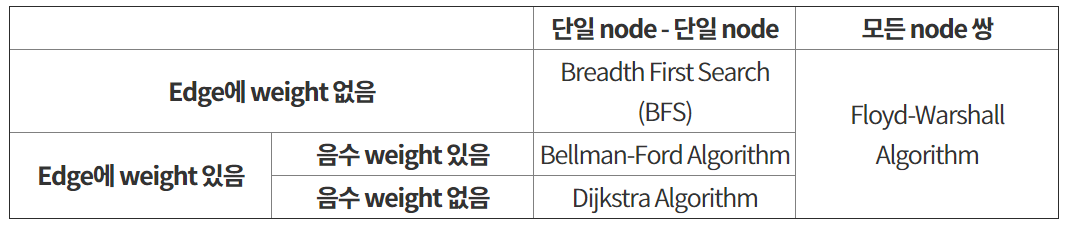
weight은 간선간의 가중치를 의미하고 단일 node - 단일 node 는 특정 출발점이 지정 되고 도착점 역시 마찬가지인 경우를 의미한다.
모든 node 쌍 의 경우에는 말 그래도 모든 쌍의 단일 node - 단일 node에 대해 찾는 것이다. (1,2) , (2,1)... 위의 문제는 1에서 모든 노드로 순회하면 돌면 되기 때문에 BFS를 채택 하였다.
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
int solution(int n, vector<vector<int>> edge) {
int answer = 0;
vector<vector<int>> N(n+1, vector<int>()); //노드 정보
vector<bool> visit(n+1, false); // 방문 기록
vector<int> dist_cnt(n+1, 0); // 간선 거리
queue<int> q; // bfs에 들어갈 큐
for (int i = 0; i < edge.size(); i++)
{
N[edge[i][0]].push_back(edge[i][1]);
N[edge[i][1]].push_back(edge[i][0]);
} // (1,2) = (2,1)이기 때문에 간선 정보를 이렇게 잡아준다.
q.push(1); // 1에서 출발
visit[1] = true;
dist_cnt[1] = 0;
while (!q.empty())
{
int start = q.front();
q.pop();
for (int i = 0; i < N[start].size(); i++) //연결된 애들 다 순회(bfs)
{
if (visit[N[start][i]] == false)//방문 안했다면
{
q.push(N[start][i]);// 다음 출발점으로 지정.
visit[N[start][i]] = true;
dist_cnt[N[start][i]] = dist_cnt[start] + 1;
}
}
}
sort(dist_cnt.begin(), dist_cnt.end());
int max = dist_cnt.back();
for (int i = 1; i <= n; i++)
{
if (dist_cnt[i] == max)
{
answer++;
}
}
return answer;
}
