문제
n가지 종류의 동전이 있다. 각각의 동전이 나타내는 가치는 다르다. 이 동전을 적당히 사용해서, 그 가치의 합이 k원이 되도록 하고 싶다. 그 경우의 수를 구하시오. 각각의 동전은 몇 개라도 사용할 수 있다.
사용한 동전의 구성이 같은데, 순서만 다른 것은 같은 경우이다.
입력
첫째 줄에 n, k가 주어진다. (1 ≤ n ≤ 100, 1 ≤ k ≤ 10,000) 다음 n개의 줄에는 각각의 동전의 가치가 주어진다. 동전의 가치는 100,000보다 작거나 같은 자연수이다.
출력
첫째 줄에 경우의 수를 출력한다. 경우의 수는 231보다 작다.
문제 해결
먼저 문제를 사람의 머리로 생각해도 바로 나오지 않았기에 bf 알고리즘은 아닐 것이라 생각했다. 그렇다면 문제를 작게 나누어 해결하는 DP 문제임을 알 수 있었다.
알고리즘
- 가치의 합이 i ( 1<= i <= k ) 이 되는 경우의 수를 dp 에 저장.
- Dp[K] 출력
코드
N , K = map(int,input().split())
coin = [int(input()) for _ in range(N)]
dp = [0 for _ in range (K+1)] # dp[i] = i원이 되는 경우의 수.
dp[0] = 1 # 동전을 1개만 쓸 때의 경우의 수를 고려하기 위해 선언.
for i in coin : # 코인 순회
for j in range(i,K+1): #dp를 순회하며
if j - i >= 0:
dp[j] += dp[j-i]
print(dp[K])
코드 해설
사실상 for 문이 본체이기 때문에 설명보다 한번 예시를 가지고 시뮬레이션을 진행해 보겠다.

👉 동전이 1원일 경우
먼저 동전이 1원일 경우 i = 1부터 , j = 1 부터 시작하게 된다. j - i = 0 이고 조건을 만족한다.
그러면 dp[1] = dp[1] + dp[0] = 0 + 1 = 1이 된다. (👉 dp[0] = 1로 설정한 이유 : 동전 하나만 사용하는 경우 카운트 위함 )
그러면 for j ~~ 문에 의해 dp[j] 에는 모두 1이 들어가게 된다.
👉 동전이 2원일 경우
i = 2 , j = 2 로 시작하여 dp[2] = dp[2] + dp[0] = 1원으로 2원만들기 + 2원 하나 쓰기 = 1+1 = 2
dp[3] = dp[3] + dp[1] = 1원으로 3원 만들기 + (1원+2원으로 3원 만들기 ) = 1 + 1 = 2
....
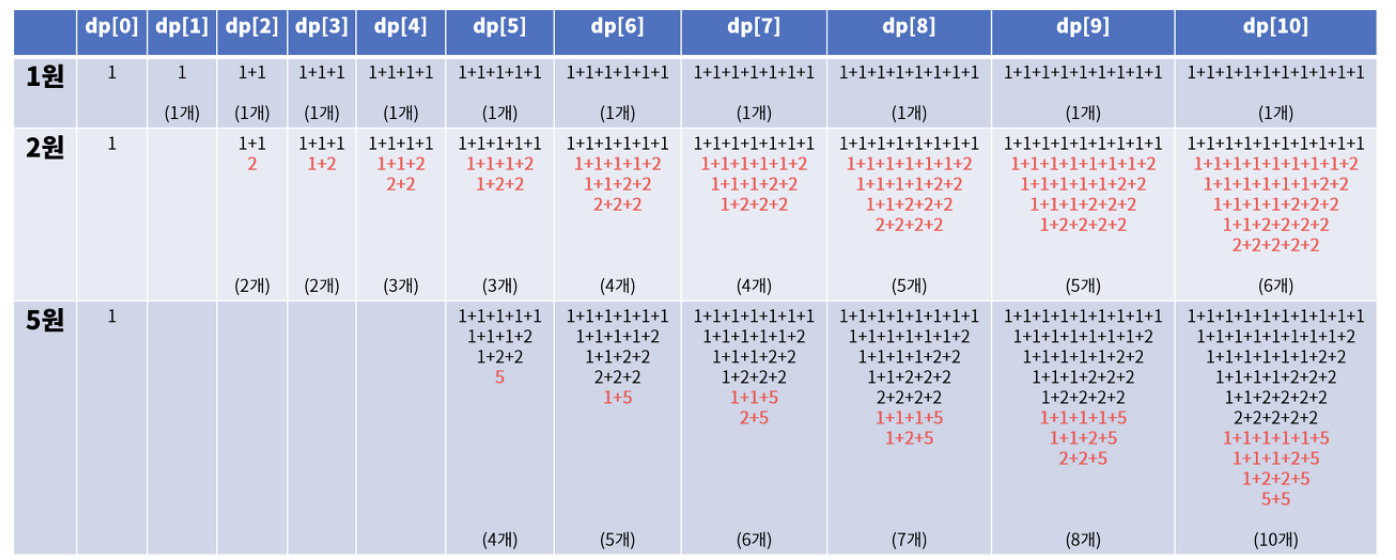
이렇게 진행하다 보면 아래와 같은 표가 나오게 된다. ( 빨간색이 새롭게 추가된 경우 )