이산수학 그래프 기본용어

이산수학 그래프2: 기본 용어

그래프

• 그래프는 정점(Vertex)의 집합과 선(Edge)들의 집합으로 구성되며 G = {V, E}로 표시한다

• 임의의 연결선 e=(u,v)에 대해서 정점(Vertex) u와 v는 서로 인접(adjacent) 했다고 하며,
  e는 정점 u와 정점 v에 접합(incident)했다고 말한다

• 연결선의 두 끝점이 같은 정점(Vertex)이면 이 연결선(Edge)을 루프(loop)라고 한다

• 두 정점의 연결선(Edge)이 두개 이상일때 다중 연결선이라고 한다

• 단순 그래프(simple graph)

  • 루프나 다중 연결선이 없는 그래프

• 차수(degree)

  • 정점u에 접합된 연결선(Edge)의 수
  • deg(u)와 같이 표기하기도 한다
  • 자기 자신을 연결하는 연결선(loop)의 경우 차수를 2로 본다

• 그래프에서 모든 정점의 차수의 합은 모든 연결선 수의 2배이다

• 두 정점 u와 v사이에 연결선이 존재하면 두 정점은 연결(connected)되었다고 한다

• 길이(length): 두 정점의 경로를 구성하는 연결선의 수

• 거리(distance): 두 정점 간의 최단 경로의 길이

• 닫힌 경로(closed path)

  • 시작점과 끝점이 같은 경로
  • 시작점에서 끝점으로 향할시 다시 시작점으로 돌아오는 경로

• 순환(사이클 cycle)

  • 3개 이상의 연결선을 갖는 경로에서 어떤 연결선도 중복되지 않는 닫힌 경로

• 부분 그래프(subgraph)

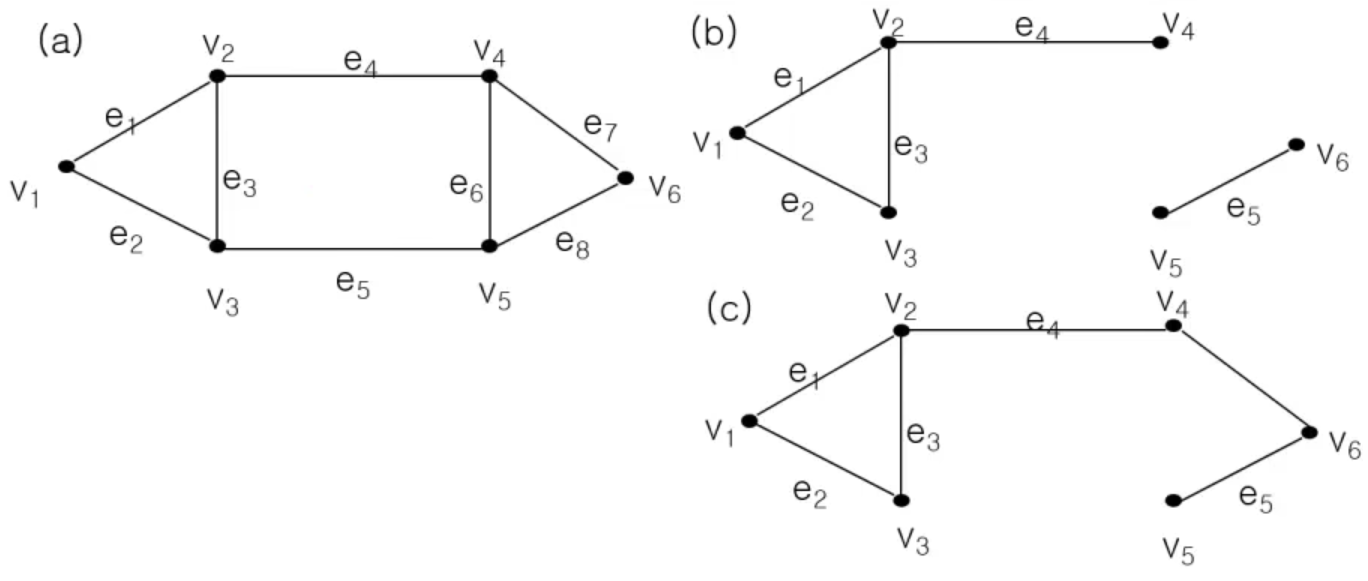
  • 그래프 G={V, E}가 있을때 V'⊆V이고, E'⊆E인 그래프 G'={V', E'}를 G의 부분그래프라고 한다
    

• 동형 그래프(isomorphic graph)

  • 그래프 G = {V, E}와 G' = {V', E'} 에 대하여, 다음 조건을 만족하는 함수가 1:1관계의 함수이면 두 그래프 G와 G'는 동현 그래프라고 한다
    함수 f: v→ v' (v∈V, v'∈V')
    (x,y) ∈ E ↔ (f(x), f(y)) ∈ E'
    그리고 이 관계가 성립하는 함수 f를 동형(isomorphic)이라고 한다
    

• 완전 그래프(complete graph)

  • 그래프 G={V, E}가 모든 정점 사이에 연결선이 존재하면 G는 완전 그래프라고 한다
    

• 이분 그래프(bipartite graph)

  • 인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프
    

• 정규 그래프 (regular graph)

  • 그래프 G={V, E}의 모든 정점의 차수가 같으면, G를 정규 그래프라고 한다.
  • 차수가 4인 정규그래프
    

• 평면 그래프(planar graph)

  • 그래프 G=(V, E)의 연결선들이 서로 교차하지 않고 평면상에 그릴수 있는 그래프G를 평면그래프라고 한다
    

• 비평면 그래프

  • 평면그래프와 반대로 교차하지 않고는 그릴수 없는 그래프

• 면(face)

  • 연결선에 따라 구분된 영역을 면이라고 한다

• 방향그래프 (directed graph)

  • 그래프 G={V,E}에서 연결선의 두 정점이 순서쌍일때 G를 방향 그래프라고 한다