이산수학

\[이산수학 강좌 1강 - 이산수학 개요 (Discrete Mathematics Tutorial For Beginners 이산수학 (Discrete Mathematics)불연속적 수학참과 거짓으로 살펴보는 컴퓨터 수학보편적인 컴퓨터 수학왜 필요한가이산수학이란 불연속적인

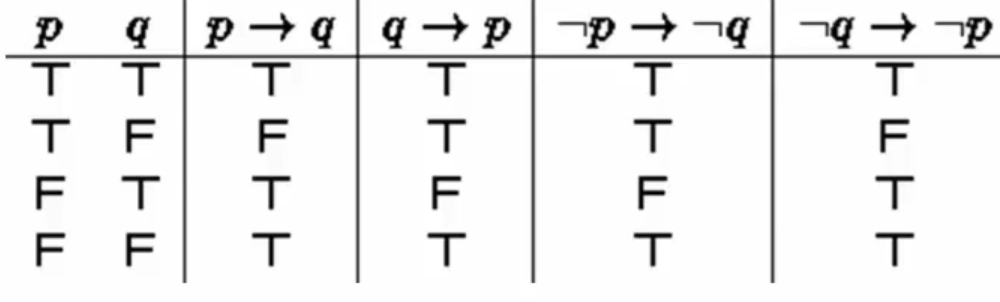
이산수학 강의, 명제1-1참 혹은 거짓을 판명할 수있는 선언적인 문장종류사실명제: 관찰, 측정, 실험으로 판단되는 명제ex)서울은 대한민국의 수도이다논리명제: 수학, 형식의 명제(컴퓨터에서 다루는 명제)복합명제: 단순명제의 조합으로 만들어지는 명제부정, Not(￢ )명

이미 "참"으로 알고있는 명제로부터 새로운 "참"인 명제를 찾아내는 과정을 통해 새로운 지식을 얻는 것 (위키백과: 어떠한 판단을 근거로 삼아 다른 판단을 이끌어 내는 것'이라고 할 수 있다.)올바른 추론의 규칙 == 논리전제(이미 "참"으로 알고있는 명제) → 결론

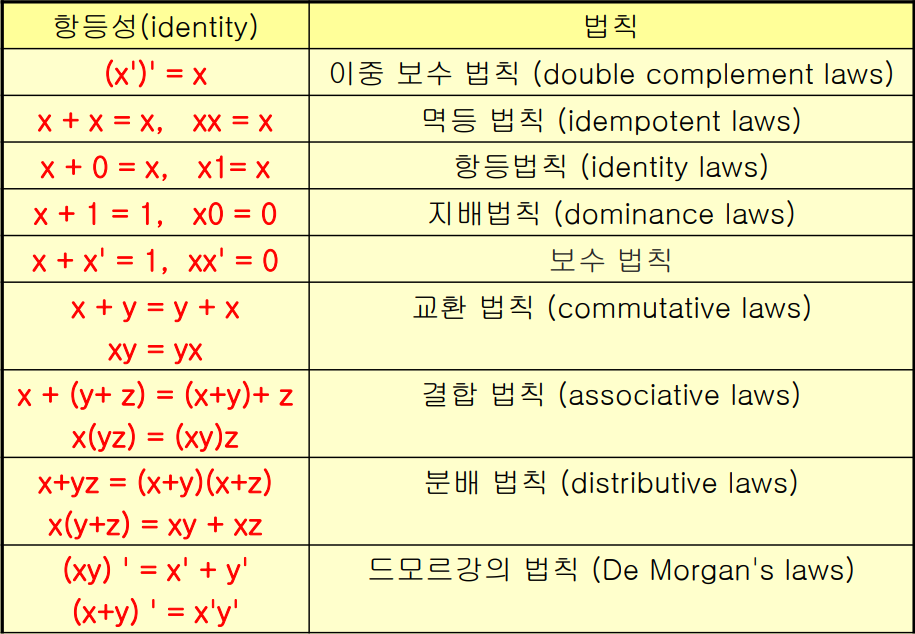
논리회로설계 문제를 푸는 과정논리회로설계 문제 → 입력,출력 정의 → 부울함수 정의 → 부울식 생성 → 부울식 최소화 → 논리회로 ⇒ 논리회로설계 문제를 풀기위해 부울대수 필요어떤 명제의 참과 거짓을 이진수 1과 0에 대

문제를 해결하기 위한 절차를 기술한 것순서대로 정의된 절차분명한 순서가 있어야 한다한 동작을 실행하면 다음 동작이 무엇인지 분명해야 한다명확성모든 동작은 명확하게 정의되어야 한다모든 동작은 실행 가능해야 한다반드시 원하는 결과가 나와야 한다일정한 시간 안에 실행되어야

이산수학 그래프1: 오일러 순환과 해밀턴 순환그래프는 정점(Vertex)의 집합과 선(Edge)들의 집합으로 구성되며 G = {V, E}로 표시한다차수(degree)정점u에 접합된 연결선(Edge)의 수deg(u)와 같이 표기하기도 한다자기 자신을 연결하는 연결선(lo

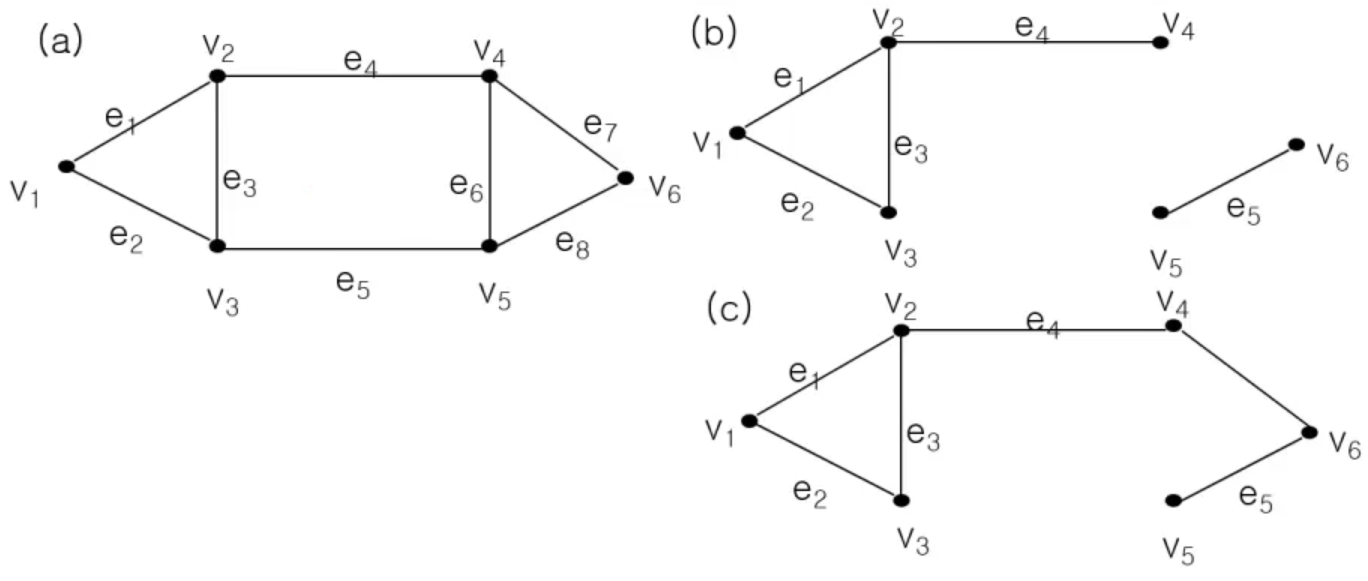
이산수학 그래프2: 기본 용어그래프는 정점(Vertex)의 집합과 선(Edge)들의 집합으로 구성되며 G = {V, E}로 표시한다임의의 연결선 e=(u,v)에 대해서 정점(Vertex) u와 v는 서로 인접(adjacent) 했다고 하며,e는 정점 u와 정점 v에 접

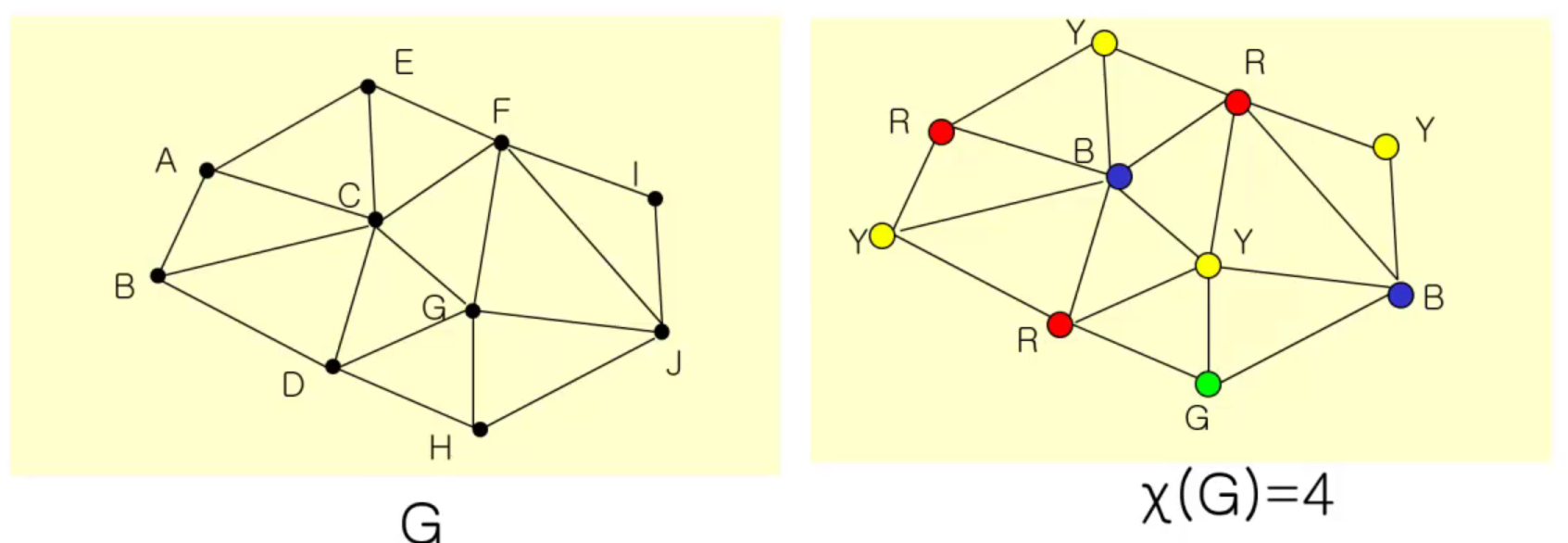
이산수학 그래프3: 그래프 채색(coloring)인접하고 있는 정점들을 서로 다른 색을 갖도록 하면서 그래프의 모든 정점에 색을 당색상수그래프 채색에 필요한 최소한의 색의 수x(G)로 표시한다 (ex. 4개 필요한 경우 x(G)=4)완전 그래프에서의 색상수x(k5) =

이산수학 그래프4: 최소신장 트리(minimum spanning tree)그래프 G = {V, E} 에서 V의 모든 정점을 포함하면서 순환(cycle)이 존재하지 않는 부분 그래프(subgraph)를 신장 트리라고 한다최소 신장 트리 ( Minimum Spanning

이산수학 그래프5: 최단경로 알고리즘(1)One → One : MST알고리즘One → all : 다익스트라, 벨만포드all → all : 플루이드워샬한 정점에서 다른 모든 정점으로의 최단경로를 찾는 알고리즘방향그래프, 비방향그래프 모두 적용 가능가중치값이 음수가 아니어

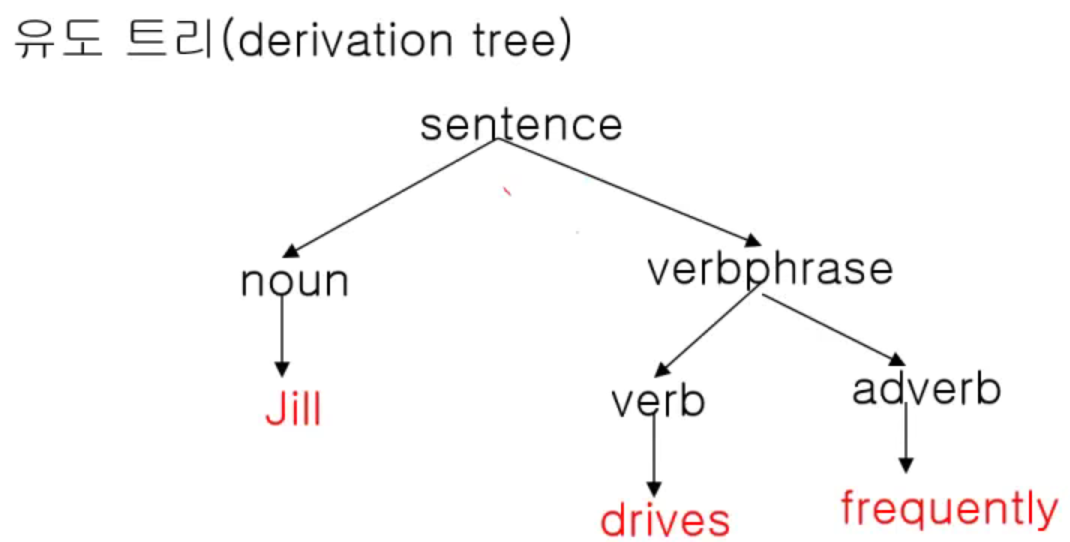
이산수학: 형식언어와 오토마타1- 형식언어와 문법S: 기호들의 집합S\*: S로부터 만들어지는 모든 유한 문자열들언어의 세가지 구성요소알파벳: 기호들의 집합 S가 반드시 존재한다.Syntax(문법): S로부터 몬장들의 집합 S\*를 형성하는 규칙이 반드시 존재한다Sem

이산수학: 형식언어와 오토마타2 - 정규식과 정규문법I : 기호(symbol)들의 집합(알파벳)I\* : 집합 I의 기호들을 결합하여 만들어지는 유한 크기를 갖는 모든 문자열의 집합λ : 공 문자열(empty string)αβ : 문자열 α와 문자열 β의 연결 (con

이산수학: 형식언어와 오토마타3- 유한상태기계(finite state machine)플립플롭이 대표적인 예시임유한 상태 기계 (S, I, F)S: 상태의 집합 (a set of states) I: 입렵값의 집합 (a set of inputs) f: 상태 추이 함수(