언어
- S: 기호들의 집합
- S*: S로부터 만들어지는 모든 유한 문자열들
- 언어의 세가지 구성요소
- 알파벳: 기호들의 집합 S가 반드시 존재한다.
- Syntax(문법): S로부터 몬장들의 집합 S*를 형성하는 규칙이 반드시 존재한다
- Semantics(의미론): 규칙에 합당하게 만들어진 문장들이 어떤 의미를 갖는지를 결정할 수 있어야 한다
- 문법: 문장의 적합한 구성에 대한 규정 / 나는 가고있다 빠른 사람 (문법에 맞지않음)
- 의미론: 문장의 적합한 의미에 대한 규정 / 소리가 걸어간다 (의미론적으로 맞지않음)
형식언어
- 특정한 법칙들에 따라 적절하게 구성된 문자열들의 집합
- 심벌(symbol): 기호
- 알파벳(alphabet): 기호들의 유한 집합
- 문자열(String): 알파벳에 포함된 기호들이 나열된 것
- 공 문자열(empty String): 길이가 0인 문자열, λ로 표시 (공집합과는 다르다.)
구 구문 문법 (phase-structure grammar)
- G = (V,T,S,P)
- V: 기호의 집합 = (단말기호(T), 비단말기호(N)로 이루어짐, V=T∪N)
- T: 단말 기호(terminal symbol) = 최종적으로 문자열로 나타내어지는 것
- S: 시작기호(start symbol, seed) = 여기서부터 문자열이 생성 됨
- P: 생성규칙(production rule) (⇒로 표시)
ex1)
⇒ (비단말기호들로 이루어짐, 이런형태가 생성규칙임)
⇒ Jill
⇒ Jill drives frequently (단말 기호 생성완료)
-
유도트리를 이용해 생성과정 표현
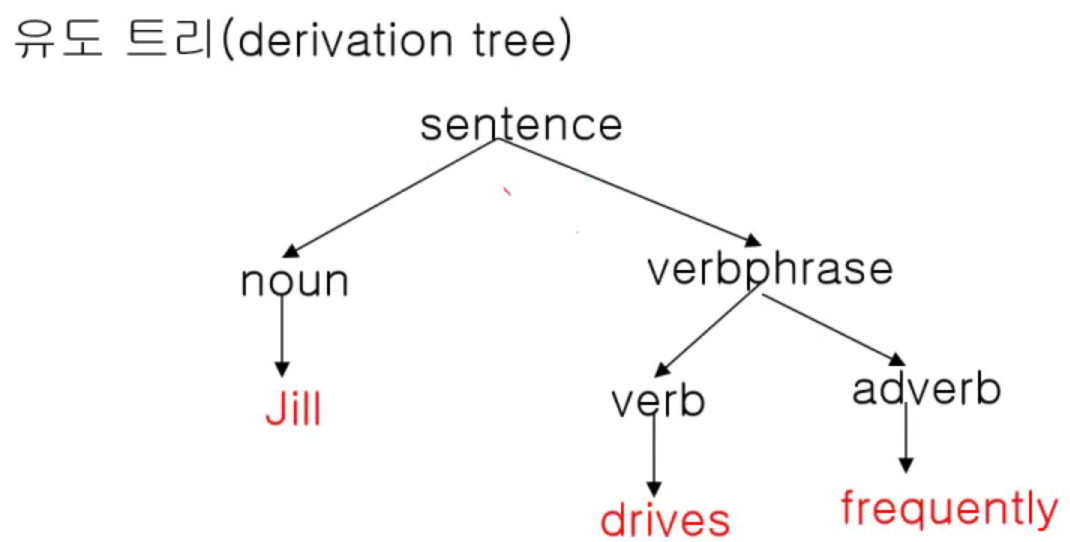
ex2)
G = (V,T,S,P)
N = {S},
T = {a, b}, V = T∪N
P = {S ⇒ aSb, S ⇒ ab}
a^3b^3은 이 문법에서 만들어지는가?
S⇒ aSb ⇒ aaSbb ⇒ aaabbb
생성 가능함
언어와 문법
- L(G): 문법 G의 언어
- 문법 G를 사용하여 만들어질 수 있는 문장들의 집합
예)
G = (V,T,S,P)
N = {S, A},
T = {a, b}, V = T∪N
P = {S ⇒ aA, S ⇒ b, A⇒aa}
S ⇒ aA ⇒ aaa
S ⇒ b
2가지 경우가 존재
따라서 문법 G로부터 유도되는 언어는
L(G) = {aaa, b}
이다
- 문법의 종류
- 유형0 문법 (비제한 문법)
- 생성에 아무 제약이 없다
- 왼쪽편에 여러개의 비단말 기호가 나올 수 있음
- 유형1 문법 (문맥 의존 문법: context sensitive grammar)
- αAβ ⇒ αγβ
- α, β ∈ (N∪T), A∈N, γ∈(N∪T) - {λ}
- 왼쪽편에 여러개의 비단말 기호가 나올 수 있음
- 왼쪽꺼가 오른쪽과 연관되어 대체됨(그래서 문맥의존 이라함)
- 유형2 문법 (문맥 자유 문법: context free grammar)
- A⇒α, A∈N (비단말 기호), α∈(N∪T)*
- 왼쪽편에 한개의 비단말 기호만 가능
- 오른쪽 편에 아무거나 나와도 가능
- 유형3 문법(정규 문법: reqular grammar)
- A⇒aB 혹은 A⇒a 혹은 A⇒λ, A, B∈N, a∈T
- 왼쪽편에 한개의 비단말 기호만 가능
- 오른쪽 편에 정해진 형태만 가능
- 유형0> 유형1> 유형2> 유형3
- 프로그래밍 언어의 경우 유형 2, 유형 3로 전부 표현됨
- 유형0 문법 (비제한 문법)
문법의 표현
-
BNF(Backus-Naur Form) 형식
-
문법 다이어그램(syntax diagram)
-
유도 트리(derivation tree)
-
BNF형식
-
비단말 기호는 <a>로 표시한다
-
생성 ⇒ 은 ::=로 표시한다
-
하나의 비단말 기호로부터 생성되는 여러 개의 문자열은 | 으로 구분한다
예시)
<v> ::= a<w>
<w> ::= bb<w>|c
-
-
문법 다이어그램
- 비단말 기호는 사각형으로, 단말 기호는 원으로 그린다.
- 생성 과정은 화살표로서 표시한다.
- 하나의 비단말 기호로부터 생성되는 여러 개의 문자열은 병롤로 놓고 화살표로 표시한다
