Graph
그래프는 데이터의 요소들이 노드(Node)로 표현되고, 이 노드들 사이의 관계를 간선(Edge)으로 연결한 구조를 가진다.
컴퓨터 과학에서 그래프는 네트워크, 소셜 미디어 상호작용, 웹사이트의 페이지 구조 등 다양한 현실 세계의 문제를 모델링하는 데 널리 사용된다.
Graph Search Algorithm
그래프를 효과적으로 탐색하고 분석하는 것은 알고리즘의 세계에서 중요한 주제 중 하나이다.
그래프 탐색 알고리즘은 그래프의 모든 노드를 체계적으로 검사(탐색)하기 위한 방법을 제공하며,
이를 통해 경로 찾기, 사이클 검출, 연결 요소 찾기 등의 다양한 문제들을 해결할 수 있다.
그래프 탐색 알고리즘은 크게 두 가지로 나눌 수 있다.
- 깊이 우선 탐색 (Depth-First Search, DFS)
- 너비 우선 탐색 (Breadth-First Search, BFS)
DFS는 노드를 가능한 한 깊숙이 탐색하다가 막히면 되돌아가 다른 경로를 탐색하는 방식으로, 미로 찾기나 퍼즐 게임같은 문제에 적합하하다.
반면, BFS는 레벨별로 노드를 탐색하며 최단 경로를 찾는 데 유용하게 사용된다.
깊이 우선 탐색 (Depth-First Search, DFS)
DFS는 그래프의 모든 노드를 방문하기 위한 그래프 탐색 알고리즘이다.
이 방법은 노드를 방문하고, 갈 수 있는 한 깊게 노드를 탐색해 나가다가 더 이상 탐색할 수 없는 지점에 도달하면,
가장 최근에 탐색했던 분기점으로 돌아가서 다른 경로를 탐색하는 방법으로 진행된다.
이러한 방식 때문에 'Backtracking'이라고도 불린다.
DFS를 구현하는 방식에는 크게 재귀(recursion)를 이용하는 방법과 스택(stack)을 이용하는 방법이 있다.
재귀를 이용한 DFS
재귀를 이용해 DFS를 구현할 때에는 현재 노드를 방문 처리하고, 현재 노드에 인접한 노드 중에서 방문하지 않은 노드에 대해 재귀적으로 진행한다.
재귀 호출은 스택의 동작을 모방한다.
아래 함수는 dict로 표현된 그래프(graph)와 현재 노드(v) 그리고 방문 여부를 확인할 리스트(visited)를 인자로 받아
DFS를 수행한 뒤 노드 방문 순서를 리스트 형태로 return한다.
def recursive_dfs(graph:dict, v:int, visited:list) -> list:
visited.append(v) # 현재 노드 방문 처리
for i in graph[v]: # 현재 노드와 인접 노드
if i not in visited: # 방문하지 않은 노드라면
recursive_dfs(graph, i, visited) # 재귀적으로 dfs 진행
return visited # 방문 순서 return
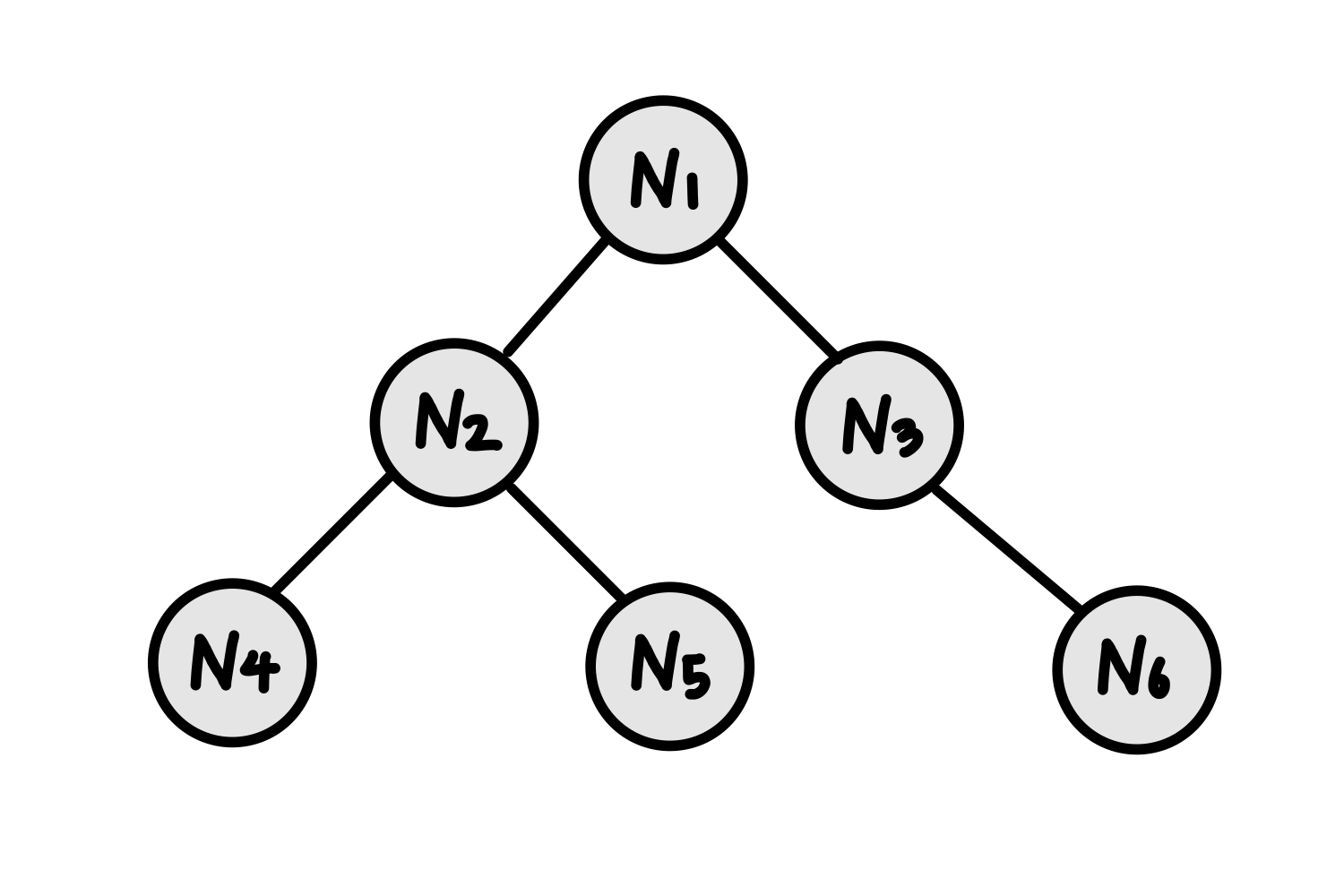
# test case (위의 그림에 나오는 그래프를 인접 리스트로 표현)
graph = {
1: [2, 3],
2: [1, 4, 5],
3: [1, 6],
4: [2],
5: [2],
6: [3],
}
print(recursive_dfs(graph, 1, [])) # [1,2,4,5,3,6]스택을 이용한 DFS
스택을 사용해 DFS를 구현할 때에는 초기 시작 노드를 스택에 넣어놓고, 스택이 빌 때까지 다음의 과정을 반복한다.
스택에서 하나의 노드를 꺼내(pop) 방문 처리하고, 해당 노드에 인접한 노드 중 방문하지 않은 노드를 스택에 추가(push)한다.
def stack_dfs(graph:dict, v:int) -> list:
visited = [] # 방문 여부 리스트
stack = [start] # 스택에 초기 시작 노드 추가
while stack: # 스택이 빌 때까지 반복
vertex = stack.pop() # 스택에서 하나의 노드를 꺼냄
if vertex not in visited: # 방문하지 않은 노드라면
visited.append(vertex) # 방문 처리
stack.extend(reversed(graph[vertex])) # 인접한 노드들의 방문 순서를 지키기 위해 역순으로 스택에 추가(extend)
return visited # 방문 순서 return
# test case
graph = {
1: [2, 3],
2: [1, 4, 5],
3: [1, 6],
4: [2],
5: [2],
6: [3],
}
print(stack_dfs(graph, 1) # [1,2,4,5,3,6]DFS의 활용
DFS는 여러가지 문제 해결에 사용된다. 예를 들어, 연결 요소 찾기, 사이클 검출, 경로 탐색, 그래프의 레이아웃 계산 등에 사용될 수 있다.
그래프의 구조를 파악하는 데 특히 유용하며, 퍼즐 게임이나 미로 찾기 같은 문제에서도 널리 사용된다.
너비 우선 탐색 (Breadth-First Search, BFS)
BFS도 그래프의 모든 노드를 방문하는 데 사용되는 알고리즘으로, 시작 노드에서 가장 가까운 노드부터 차례대로 모든 노드를 방문하는 형식이다.
BFS는 주로 큐(queue)를 사용하여 각 노드를 순차적으로 탐색하고, 각 노드와 인접한 노드들을 다시 큐에 추가하는 방식으로 그래프를 탐색한다.
너비 우선 탐색 알고리즘은 최단 경로를 찾거나 그래프를 레벨별로 탐색할 때 유용하다.
BFS의 기본 원리
- 큐 초기화 : 시작 노드를 큐에 넣는다.
- 노드 방문 및 큐에서 제거 : 큐의 맨 앞 노드를 꺼내 방문 처리한다.
- 인접 노드 탐색 : 방문한 노드와 인접한 모든 노드를 확인하고, 아직 방문하지 않은 노드를 큐에 추가한다.
- 반복 실행 : 큐가 비어있을 때 까지 위의 과정을 반복한다.
BFS 구현 (using deque)
from collections import deque
def bfs(graph:dict, start:int, visited:list) -> list :
dq = deque([start]) # 시작 노드를 큐에 추가
visited.append(start) # 시작 노드 방문 처리
while dq: # 큐가 빌 때 까지 반복
v = dq.popleft() # 큐의 맨 앞 노드 pop
for i in graph[v]: # pop한 노드와 인접한 노드들
if i not in visited: # 방문하지 않은 노드라면
dq.append(i) # 큐에 추가하고
visited.append(i) # 방문 처리
return visited
# test case
graph = {
1: [2, 3],
2: [1, 4, 5],
3: [1, 6],
4: [2],
5: [2],
6: [3],
}
print(bfs(graph, 1, [])) # [1,2,3,4,5,6]
위의 코드에서 collections 모듈의 deque 객체를 사용하는 이유는 list 객체의 pop() 함수 사용보다 deque의 popleft() 함수가 효율적으로 동작하기 때문이다.
deque.popleft() vs. list.pop(0)
collections 모듈의 deque 객체는 양쪽 끝에서 요소를 추가하거나 제거할 수 있도록 설계된 자료구조로, 이중 연결 리스트로 구현된다.
deque.popleft()는 deque의 맨 앞 요소를 제거하는 연산으로, 이 연산은 상수 시간인 O(1)에 수행된다. 따라서 요소의 수에 관계없이 항상 일정한 성능을 유지한다.
반면, Python의 list 객체는 동적 배열로 구현되어 있다. list.pop(0)을 사용하면 리스트의 첫 번째 요소를 제거하고, 나머지 요소들을 한 칸씩 옆으로 이동시켜야 한다. 이 작업은 O(N)의 시간 복잡도를 가지며, 리스트의 크기가 클수록 느려진다.
BFS의 활용
- 최단 경로 찾기 : BFS는 가중치가 없는 그래프에서 두 노드 간의 최단 경로를 찾는 데 사용될 수 있다.
또한, 레벨 별로 탐색하므로 계층적 구조를 갖는 문제 해결에 적합하다. - 연결 요소 : 그래프 내에서 각각 독립적으로 연결된 부분을 찾는 데 사용된다.
- 사이클 검증 : BFS를 이용하여 그래프 내 사이클의 존재 여부를 확인할 수 있다.
with GPT-4

