수열 기본

수열

규칙성을 가지고 나열되어 있는 수들

수열의 합

Sn = a1 + a2 + a3 + ....

특정 항의 값

an = Sn - S(n-1)

---

📝등차수열 이론

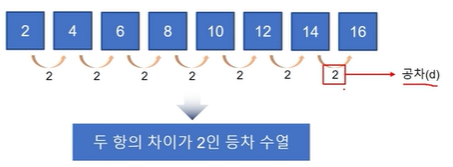
등차수열

연속된두 항의 차이가 일정한 수열

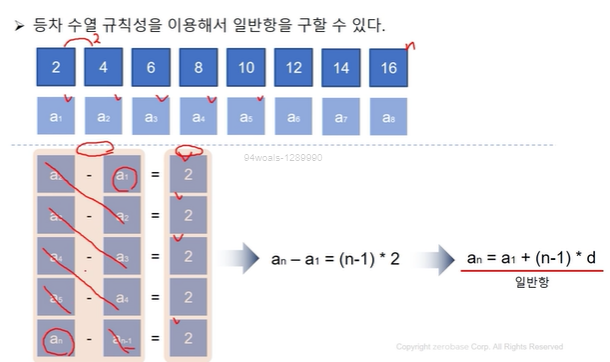
(1) 등차수열 일반항

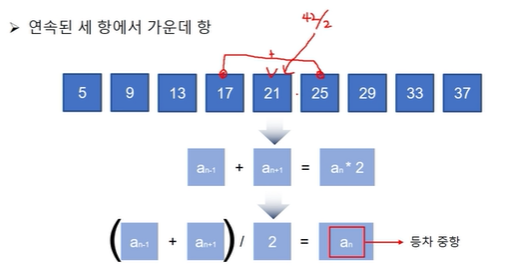
(2) 등차 중항

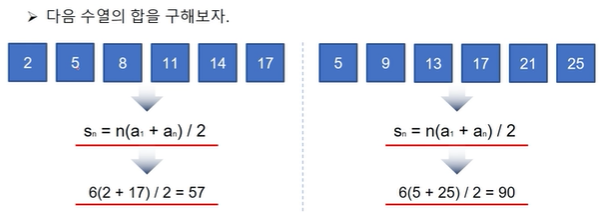
(3) 등차수열의 합

** 실습

---

💻 파이썬

등차수열 (n번째 항 값)

Q> 다음 수열을 보고 n번째 항의 값을 출력하는 프로그램을 만들어보자.

• an = {2,5,8,11,14,17,20,23,26,29, ...}
  
  

🏷️ 풀이 방법(1)

inputN1 = int(input('첫번째 항 a1 입력 : '))
input0 = int(input('공차 d 입력 : '))
inputN = int(input('알고싶은 n항 입력 : '))

valueN = 0
n = 1

while n <= inputN:
    if n == 1:
        valueN = inputN1
        print('{}번째 항의 값 : {}' .format(n, valueN))
        n += 1
        continue

    valueN += input0
    print('{}번째 항의 값 : {}' .format(n, valueN))
    n += 1

print('{}번째 항의 값 : {}' .format(inputN, valueN))

첫번째 항 입력
공차 입력
알고싶은 n(몇 번쨰에 해당하는 n값) 입력

n번째 항의 값을 valueN 이라는 변수를 사용하겠다, 선언
첫 번째 항부터 시작해야 하기 때문에, n은 1부터 시작, 선언

n이 알고싶은 항(inputN)값 보다 작거나 같을 떄 까지 반복한다
    첫번쨰 항의 경우
        '첫번째 항'과 동일하다, 할당
        '첫번째 항'의 값 출력
        n에 1을 더해주고
        위로 다시 올라감

    n이 2(2번째 항) 부터
    출력 : '첫번쨰 항' + 공차 = 2번쨰 항의 값
    n에 1을 더해줌
    
n번째 항 값 출력

🏷️ 풀이 방법(2)

inputN1 = int(input('첫번째 항 a1 입력 : '))
input0 = int(input('공차 d 입력 : '))
inputN = int(input('알고싶은 n항 입력 : '))

valueN = 0

valueN = inputN1 + (inputN-1) * input0
print({}번째 항의 값 : {}' .format(inputN, valueN))

(1) 첫번째 항 입력
(2) 공차 입력
(3) 알고싶은 n(몇 번쨰에 해당하는 n값) 입력

(4) n번째 항의 값을 valueN 이라는 변수를 사용하겠다, 선언

(5) 틍차수열의 공식 활용 : an = a1 + (n-1)d
(6) n번째 항 값 출력

등차수열 (합)

Q> 다음 수열을 보고 n번째 항 까지의 합을 출력하는 프로그램을 만들어보자.

• an = {2,5,8,11,14,17,20,23,26,29, ...}
  
  

🏷️ 풀이 방법(1)

inputN1 = int(input('첫번째 항 a1 입력 : '))
input0 = int(input('공차 d 입력 : '))
inputN = int(input('알고싶은 n항 입력 : '))

valueN = 0
sumN = 0 ✔️
n = 1

while n <= inputN:
    if n == 1:
        valueN = inputN1
        sumN += valueN ✔️
        print('{}번째 항의 값 : {}' .format(n, valueN))
        n += 1
        continue

    valueN += input0
    sumN += valueN ✔️
    print('{}번째 항의 값 : {}' .format(n, valueN))
    n += 1

print('{}번째 항의 값 : {}' .format(inputN, valueN))

(추가) sumN = 0 
(추가) sumN += valueN

🏷️ 풀이 방법(2)

inputN1 = int(input('첫번째 항 a1 입력 : '))
input0 = int(input('공차 d 입력 : '))
inputN = int(input('알고싶은 n항 입력 : '))

valueN = 0
sumN = 0 ✔️

valueN = inputN1 + (inputN-1) * input0
sumN = inputN * (inputN1 + valueN) / 2 ✔️
print('{}번째 항의 값 : {}'.format(inputN, valueN))

(1) 첫번째 항 입력
(2) 공차 입력
(3) 알고싶은 n(몇 번쨰에 해당하는 n값) 입력

(4) n번째 항의 값을 valueN 이라는 변수를 사용하겠다, 선언
(5) n번째 항 까지의 합을 sumN으로 선언

(6) 틍차수열의 공식 활용 : an = a1 + (n-1)d
(7) 틍차수열 합 공식 활용 : sn = n(a1 + an) /2
(8) n번째 항까지의 합 값 출력

---

참고/출처 제로베이스 데이터 스쿨