📝등비수열 이론

등비수열

연속된두 항의 비가 일정한 수열

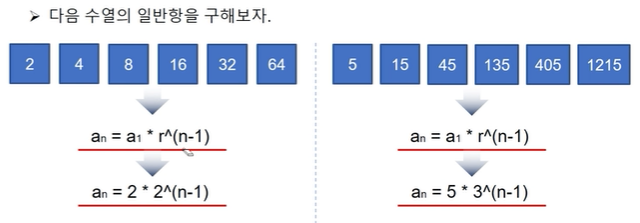
일반항

an = a1 * r^(n-1)

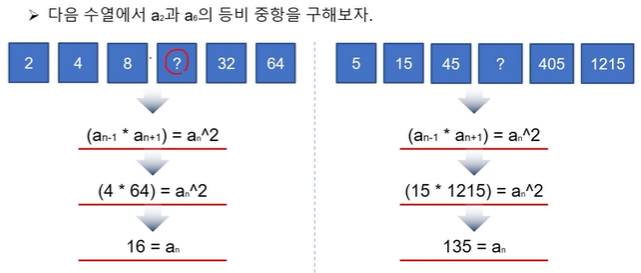
등비중항

an^2

등비수열 합

sn = a1 * (1-(r^n) / (1-r)

---

💻 파이썬

등비수열 (n번째 항 값)

다음 수열을 보고 n번째 항의 값을 출력하는 프로그램을 만들어보자.

• an = {2,4,8,16,32,64,128,256...}

🏷️ 풀이 방법(1)

inputN1 = int(input('a1  입력 : '))
inputR = int(input('공비 r  입력 : '))
inputN = int(input('n  입력 : '))

valueN = 0
n = 1

while n <= inputN:
    if n == 1:
        valueN = inputN1
        print('{}번째 항의 값 : {}' .format(n,  valueN))
        n += 1
        continue

    valueN *= inputR # == ( valueN = valueN * inputR)
    print('{}번째 항의 값 : {}'.format(n, valueN))
    n += 1
    
print('{}번째 항의 값 : {}'.format(inputN, valueN))

1번째 항 입력 요청
공비 입력 요청
알고싶은 n항 의 값 요청

n에 해당되는 최종 값을 valueN으로 선언
무한루프에 빠지지 않기 위해 n 선언

n이 '알고싶은 n항 의 값'보다 작거나 같을 때 까지 반복
    n이 1인 경우 = 1항인 경우  (조건)
        사용자가 입력한 1번쨰 항은 valueN과 같다
        바로 출력
        무한루프에 빠지지 않기 위해 +1
        위로 올라감

    n이 2가 되는 순간, 공비를 곱하고  다시 자신에게 할당 함
    출력
    무한루프에 빠지지 않기위해 +1

🏷️ 풀이 방법(2)

✔️ 공비수열 공식 활용 : an = a1 * r^(n-1)

inputN1 = int(input('a1  입력 : '))
inputR = int(input('공비 r  입력 : '))
inputN = int(input('n  입력 : '))

valueN = 0
n = 1

valueN = inputN1 * (inputR **(inputN-1)) ✔️
print('{}번째 항의 값 : {}'.format(inputN, valueN))

---

등비수열 (합)

Q> 다음 수열을 보고 n번째 항 까지의 합을 출력하는 프로그램을 만들어보자.

• an = {2,4,8,16,32,64,128,256...}
  
  

🏷️ 풀이 방법(1)

inputN1 = int(input('a1  입력 : '))
inputR = int(input('공비 r  입력 : '))
inputN = int(input('n  입력 : '))

valueN = 0
sumN = 0 ✔️
n = 1

while n <= inputN:
    if n == 1:
        valueN = inputN1
        sumN += valueN ✔️
        print('{}번째 항의 값 : {}' .format(n,  valueN))
        n += 1
        continue

    valueN *= inputR # == ( valueN = valueN * inputR)
    sumN += valueN ✔️
    print('{}번째 항의 값 : {}'.format(n, valueN))
    n += 1

print('{}번째 항의 값 : {}'.format(inputN, valueN))

(추가) sumN = 0 
(추가) sumN += valueN

🏷️ 풀이 방법(2)

inputN1 = int(input('a1  입력 : '))
inputR = int(input('공비 r  입력 : '))
inputN = int(input('n  입력 : '))

valueN = 0
sumN = 0
n = 1

sumN = inputN1 * (1 - (inputR ** inputN)) / (1-inputR)
print('{}번째 항까지의 합: {}' .format(inputN, int(sumN) )) #정수로만 보고싶을 때

# or
# print('{}번째 항까지의 합: {}' .format(inputN, isumN )) - 실수여도 상관 없을 때 

(1) 첫번째 항 입력
(2) 공비 입력
(3) 알고싶은 n(몇 번쨰에 해당하는 n값) 입력

(4) n번째 항의 값을 valueN 이라는 변수를 사용하겠다, 선언
(5) n번째 항 까지의 합을 sumN으로 선언

(6) 등비수열의 공식 활용 : an = a1 * r^(n-1)
(7) 등비수열 합 공식 활용 : sn = a1 * (1-r^n) / (1-r)
(8) n번째 항까지의 합 값 출력

---

참고/출처 제로베이스 데이터 스쿨