고유값(eigen value)

행렬의 선형 변환은 행렬 A, 또 다른 행렬 W가 있다고 하면

AW에 대해 행렬 W에 대해 선형 변환 A를 해주었다. 라고 말한다.

---

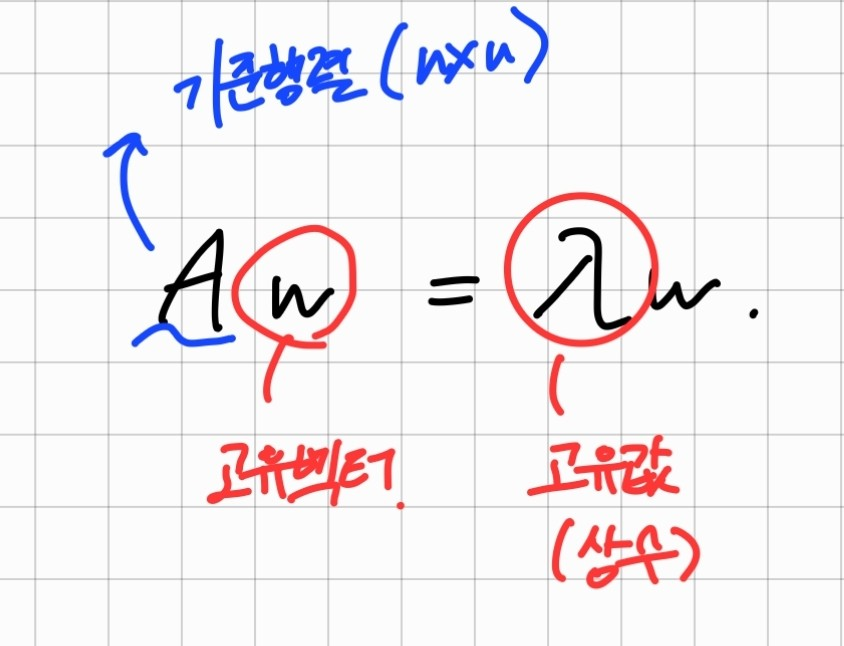
Aw = λw라는 식을 본다면 w 에 대해서 선형 변환 A를 한 값이 기존의

행렬 w에 상수(λ)배를 한 값과 같아질때, w를 고유벡터, λf를 고유값이라고 한다.

벡터를 기준으로 생각하면 벡터의 크기만 변하고 방향은 전혀 바뀌지 않았다는 말이 된다.

고유값은 정방행렬 ( N x N ) 행렬에서만 존재할 수 있는 제약조건이 있다.

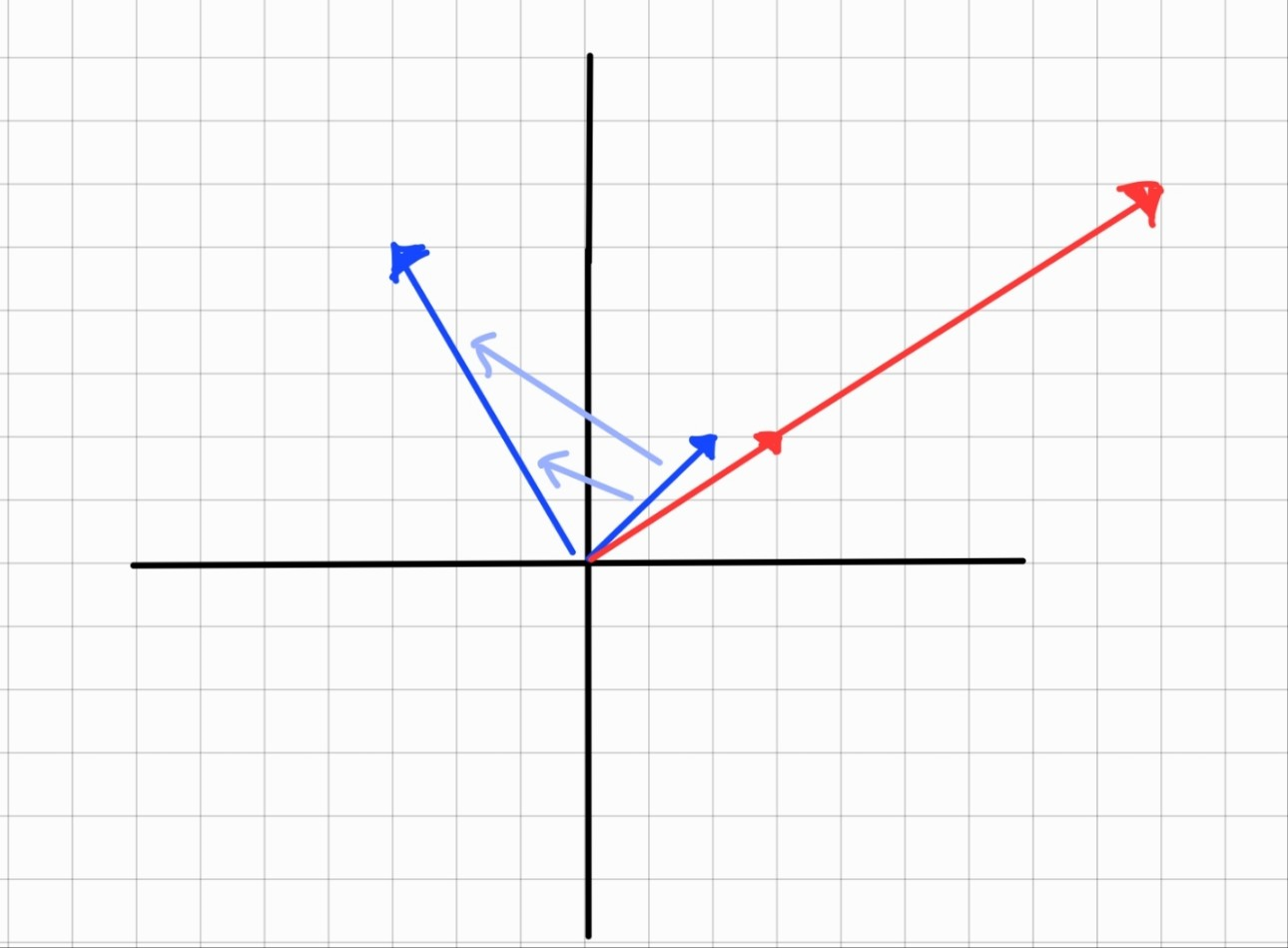
다음과 같은 벡터를 봤을때 보통의 벡터는 파란색처럼 선형 변환을 하면

크기와 방향이 전부 변한다.

하지만 빨간색처럼 방향이 같고, 크기만 다른( 정수배 ) 경우 고유값과
고유 벡터가 존재한다고 말 할 수 있다.

딥러닝에서 언제 중요할까?

PCA와 같은 차원축소기법에서 고차원 데이터를 저차원 공간으로 변환하기 위한 데이터의 주 성분을 찾는 과정에서도 이용이 됩니다.

행렬 연산을 하는 과정에서 계산에 대한 COST가 줄어든다.

PCA와 같은 차원축소기법에서 고차원 데이터를 저차원 공간으로 변환하는 과정에서 사용된다.

위와 같은 말로 고차원 데이터의 특징값을 추출하여 연산을 가볍게 하고 모델의 크기를 줄여 학습 효율을 높일 수 있습니다.