통계/수학
1.고유값(eigen value)
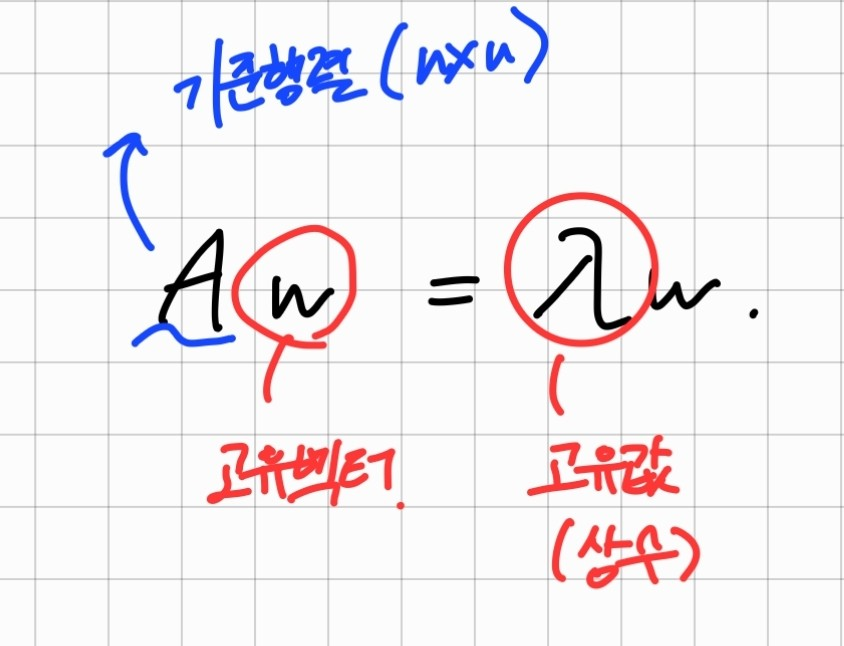
행렬의 선형 변환은 행렬 A, 또 다른 행렬 W가 있다고 하면 AW에 대해 행렬 W에 대해 선형 변환 A를 해주었다. 라고 말한다. Aw = λw라는 식을 본다면 w 에 대해서 선형 변환 A를 한 값이 기존의 행렬 w에 상수(λ)배를 한 값과 같아질때, w를 고유벡
2.샘플링 / 리샘플링
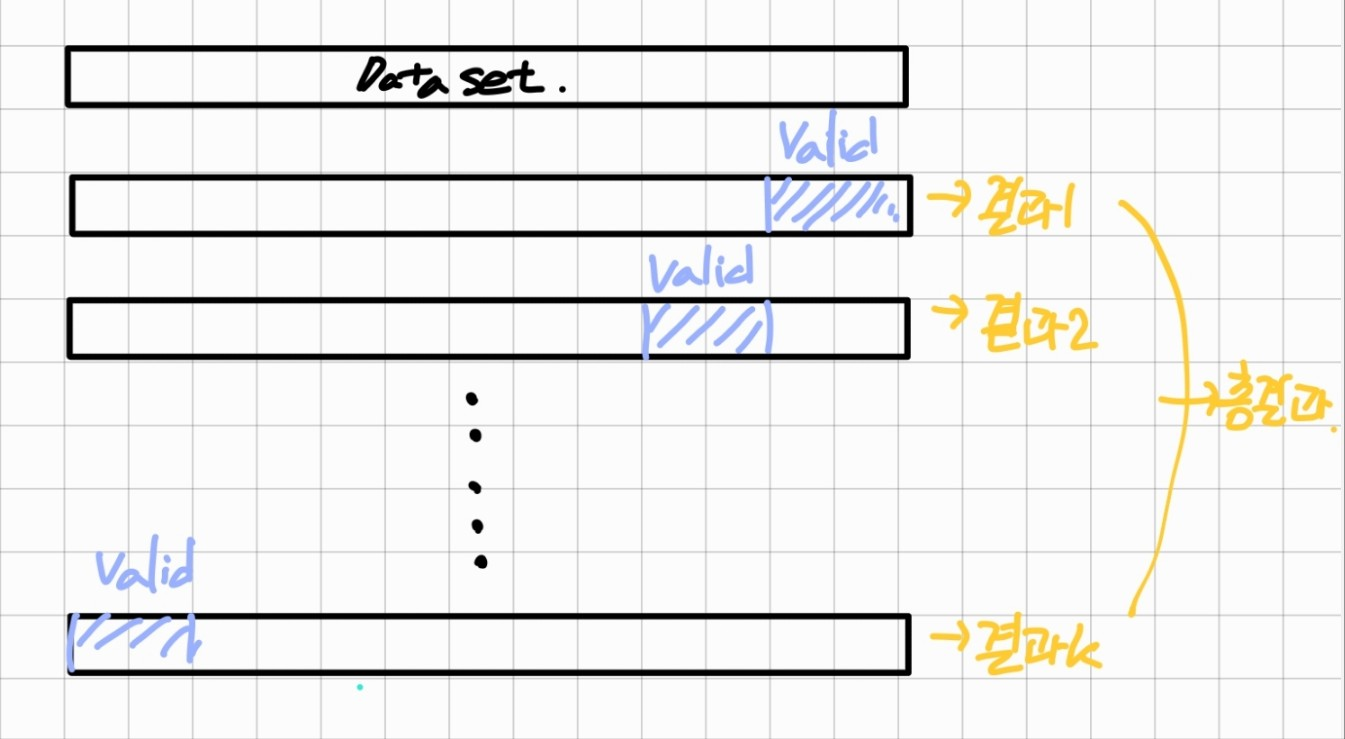
샘플링은 모집단에서 임의의 표본들을 뽑아내는 것으로 표본 추출을 의미한다. 샘플링을 하는 이유는 모집단을 전부 조사하는 것이 불가능하기 때문이다. 따라서 샘플링을 이용하여 모집단에 대한 추론을 수행한다. 추출된 표본은 가능한 모집단을 대표할 수 있는 것이 좋으며, 완
3.확률 변수와 확률 모형
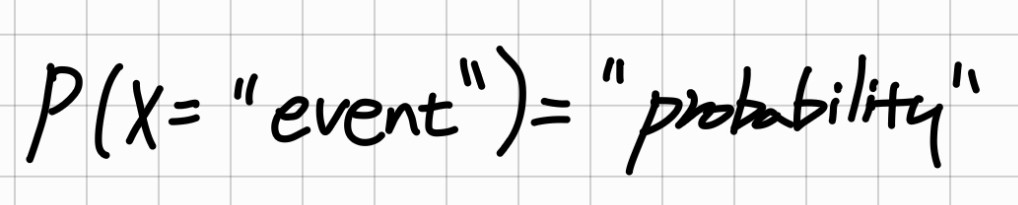
확률 변수는 EVENT 자체를 정의하는 것입니다. 확률로 표현할 수 있는 것은 정말 다양하기에 변수라는 용어를 사용합니다. 확률이 정의된 Sample space가 있고, 확률 변수를 0 $\\preceq x \\preceq 1 $ 사이로 지정하는 함수를 확률 함수라고
4.누적분포함수와 확률 밀도 함수
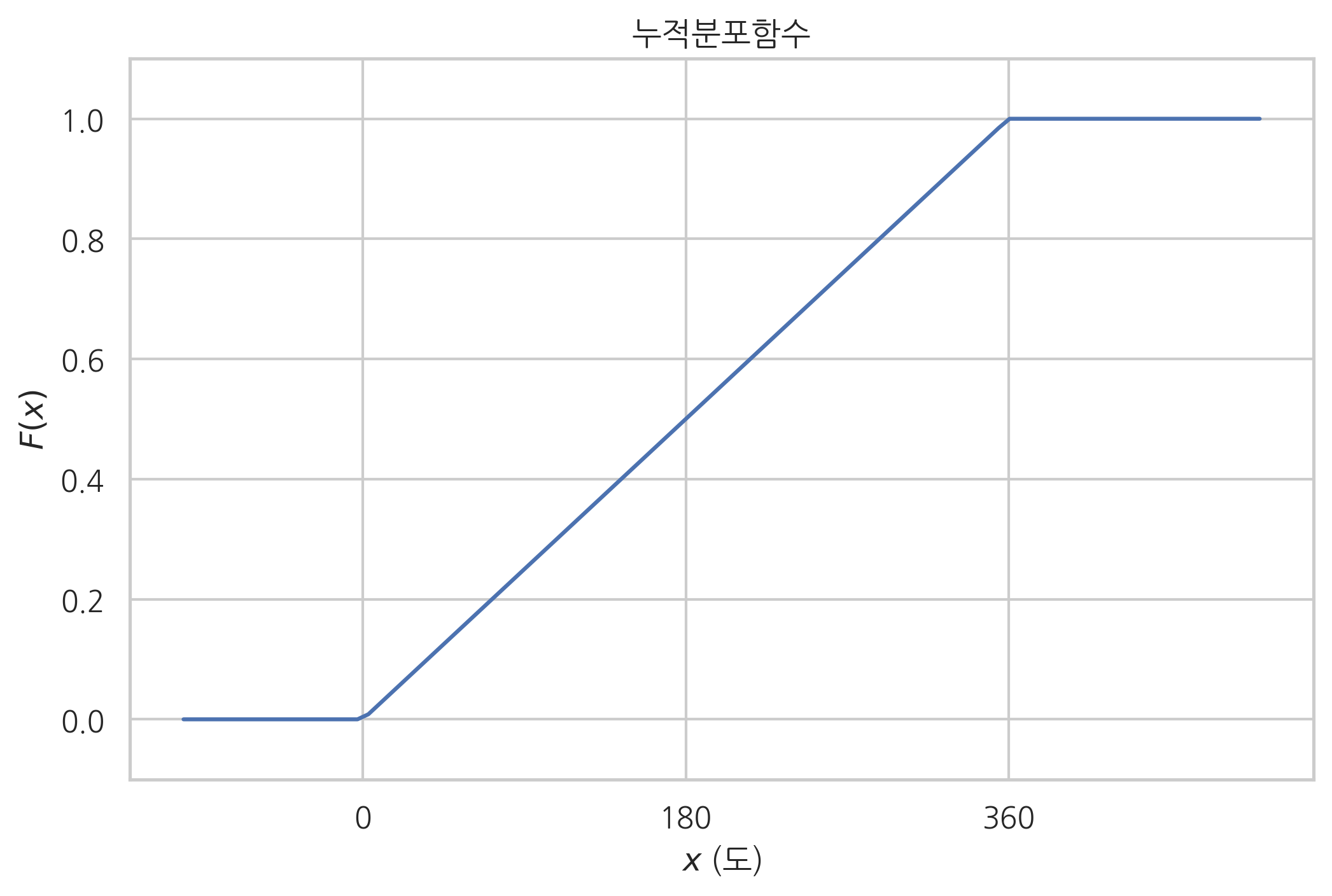
기존의 사건을 표현하기 위해서는 $ a \\leq X \\leq b $ 와 같은 방식으로 두개의 숫자가 반드시 필요했습니다. 하나의 숫자로 interval을 정의하는 방법에 대해 고민하다 나온것이 시작점을 전부 \-$\\infty$ 음의 무한대로 고정하는 것입니다.
5.조건부 확률이란.

Bayesian theory 에 입각한 확률론인 베이지안 확률론에서는 두 사건 A와 B의 관계를 알고 있다면 사건 B가 발생하였했다는 사실로부터 기존에 알고 있는 사건 A에 대한 확률 P(A)를 좀 더 정확한 확률로 바꿀 수 있는 방법을 알려준다. 이를 위해서는 결합확
6.공분산과 상관계수

다변수 확률변수 간의 상관 관계를 숫자로 나타낸 것이 공분산(covariance)과 상관계수(correlation coefficient 이다.) 표본 공분산의 경우 식으로 표현하면 다음과 같다. $$ s{xy} = \\frac{1}{N}\\sum{i=1}^N(x{i}
7.신뢰 구간
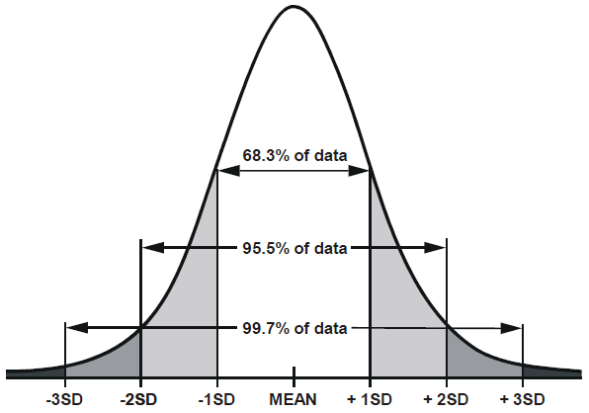
신뢰 구간
8.중심 극한 정리

중심극한 정리