DX9을 이용한 3D Game 프로그래밍 입문 - Part.1 수학적 준비

3- 공간의 벡터

벡터를 방향을 가진 선분으로 표현하며,벡터의 속성으로는 '길이'와 '가리키는 방향'의 두 가지가 있다.
즉, 벡터는 크기와 방향을 모두 가지는 물리적 양을 모델링하는 데 매우 유용 하다.

위치는 벡터의 속성이 아니므로, 다른 위치에 있더라도 동일한 길이와 방향을 가리키는 두 개의 벡터는 동일한 것으로 취급된다. 즉 평행하며 같은 길이를 가진 벡터는 서로 동일한 것으로 보면 된다.

벡터의 위치는 벡터의 속성을 변경하지 않으므로, 좌표 시스템의 원점에 꼬리가 일치하도록 벡터들을 평행하게 배치할 수 있따. 벡터의 꼬리가 원점과 일치하면 벡터가 표준점에 위치한 것이 된다.

즉, 벡터가 표준점 내에 위치하면 머리점의 좌표를 확인하는 방법으로 벡터를 기술할 수 있게 된다. 우리는 이 좌표들을 벡터의 성분이라 한다.

-NOTE-
표준점 내에 위치한 벡터의 머리 좌표를 이용하여 벡터를 기술할 수 있다는 점 때문에 포인트와 벡터를 혼돈하는 일이 있을 수 있다. 두 가지의 차이점을 강조하기 위해서 포인트와 벡터의 정의를 다시 한 번 확이하도록하자. 포인트는 좌표 시스템 내의 한 위치를 나타내는 데 반해 벡터는 크기와 방향을 가지고 있다.

영벡터 : 모든 성분에 0을 가짐. 영벡터는 굵은 0으로 표시된다 0 - (0,0,0).

-3의 표준 기저 벡터 : i,j,k로 표현되며 좌표 시스템의 x,y,z 축을따라 진행하고 모두 1의 크기를 가진다 i = (1,0,0), j =(0,1,0),
k = (0,0,1)

-NOTE-
크기로 1을 가지는 벡터를 단위 벡터라고 부른다.

D3DX 라이브러리에서는 3-공간 낸의 벡터를 표현하기 위해 D3DXVECOTR3 클래스를 이용한다.

스칼라 양과 마찬가지로 벡터역시 D3DXVECOTR3 클래스 선언에서 볼 수 있는 것처럼 자신의 산술 연산을 가지고 있다.

-NOTE-
우리가 가장 관심을 가지고 있는 것은 3D 벡터이지만, 떄로는 3D 그래픽 프로그래밍에서도 2D 와 4D 벡터를 이용할 필요가 있다. D3DX 라이브러리는 2D와 4D 벡터를 표현하기 위해 D3DVECTOR2와 D3DXVECTOR4 클래스를 제공하고 있다. 다른 차원의 벡터라고 하더라고 3D 벡터와 동일하게 크기와 방향의 두 가지 속성을 가지며, 오직 차원에만 차이가 있다. 부가적으로 벡터의 산술 연산 역시 R3에만 정의된 벡터 외적을 제외하고는 어떤 차원의 벡터에도 범용화될 수 있다. 즉, 외적을 제외하고는 우리가 설명할 3D 벡터의 모든 연산을 2D와 4D 심지어 N-차원 벡터에까지 적용할 수 있다.

벡터 상등

기하하적으로는 같은 방향과 같은 길이를 가지는 두 벡터는 동일한 것으로 보게 되지만, 대수적으로 벡터가 동일한 차원이고 대응되는 성분이 같은 경우에 두 벡터를 동일한 것으로 본다.

코드에서는 오버로드된 동등 연산자를 이용해 두 벡터가 같은지를 확인할 수 있다.

-NOTE-
부동 소수점 수를 비교할 때는 주의를 기울여야 한다. 부동 소수점의 부적황성 때문에 같은 것으로 생각되는 수라도 조금 다를 수 있기 때문이다. 따라서 두 수가 대락젹으로 같은지를 확인해야 한다. 이를 위해 매우 작은 값인 EPSILON 상수를 버퍼로 이용하는데. 두ㅜㅅ의 거리가 EPSILON보다 작을 경우 같은 것이라 말하게 된다. 다른 말로 하면, EPSILON은 부동 소수점의 부정확성을 위한 허용 한계를 제공하는 것이다. 다음의 함수는 두 개의 부동 소수점이 같은지를 테스트하는 데 EPSILON을 이용하는 방법을 보여주고 있다.

const float EPSILON = 0,001f;
bool Equals(float lhs, float rhs)
{
	return fabs(lhs -rhs) < EPSILON ? true : false;
}

D3DXVECTOR 3 클래스를 이용할 때는 오버로드된 비교 연산자가 이 작업을 대신하므로 우리가 직접 신경 쓸 필요는 없지만, 부동 소수점을 비교하는 방법에 대해서는 반드시 기억하고 있어야 한다.

벡터의 크기 게산

기하학적으로 벡터의 크기는 방향을 가진 선분의 길이이다. 벡터의 성분이 주어졌다고 할 때, 다음과 같은 식을 이용해 벡터의 크기를 대수학적으로 계산해낼 수 있다.

(1) ||U|| = 루트 (각 성분의 제곱의 합)

D3DX 라이브러라를 이용할 때는 D3DXVec3Length(&D3DVECTOR3) 함수를 통해 벡터의 크기를 계산할 수 있다.

벡터의 정규화

벡터의 정규화는 벡터의 크기를 1로 만들어 단위 벡터가 되도록 하는 것이다. 다음과 같이 벡터의 각 성분을 벡터의 크기로 나누면 정규화가 된다.

D3DX 라이브러리를 이용할 때는 다음 함수를 통해 벡터를 정규화할 수 있다.

D3DXVECTOR3 D3DXVec3Normalize(
D3DXVECTOR3 pOut, // 결과
CONST D#DXVECCTOR3* pV //정규화하려는 벡터
);

-NOTE-
이 함수는 결과를 가리키는 포인터를 리턴하므로 이를 다른 함수의 인자로 전달할 수 있다. D3DX 수학 함수는 대부분의 경우 특별히 언급하지 않는 한 결과를 가리키는 포인터를 리턴한다.

벡터 더하기

대응되는 성분을 더하면 두 개의 벡터를 더할 수 있다. 더하고자 하는 벡터는 반드시 동일한 차원을 가져야 한다는 것을 기억하자.

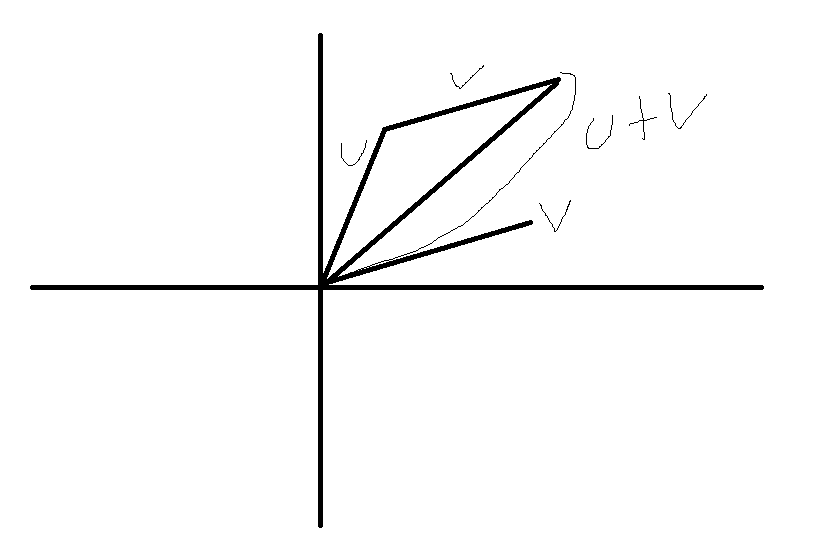
코드 내에서 벡터를 더하기 위해서는 오버로드된 덧셈 연산자를 이용한다.

벡터 빼기

더하기와 비슷하게 벡터의 대응되는 성분을 빼는 방법으로 벡터 빼기를 수행할 수 있다. 벡터는 반드시 동일한 차원을 가져야 한다.

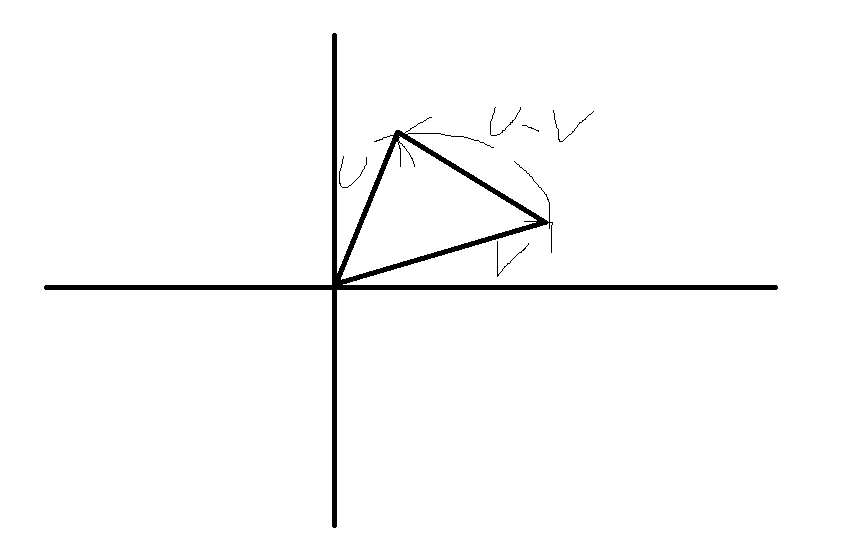
위 그림에서 알 수 있는 것처럼 벡터 빼기는 V의 머리에서 U의 머리까지의 벡터를 리턴한다. 만약 U와 V의 성분을 포인트의 좌표로 생각한다면, 벡터 빼기를 이용해 한 포인트에서 다른 포인트 까지의 벡터를 얻을 수 있다. 포인트 간의 방향을 기술하는 벡터를 얻어야 하는 경우가 많기 때문에 벡터 뺴기는 상당히 유용한 작업이다.

스칼라 곱

벡터는 스칼라로 곱하는 것이 가능하며, 짐작할 수 있겠지만 이를 통해 벡터의 배율이 변경된다. 음수로 곱을 수행하지 않는 이상 벡터의 방향은 변하지 않으며,음수를 이용하는 경우에는 벡터의 방향이 뒤집힌다.

D3DXVECTOR3 클래스는 * 스칼라 곱 연산자를 제공한다.

내적

내적은 벡터 대수학에서 정의하는 두 가지 곱셈 중 하나이며 다음과 같이 계산된다.

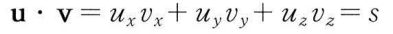
위의 식은 분명한 기하학적 의미를 보여주고 있지 않다. 코사인의 법측일 이용하면 두 벡터 간의 내적이 벡터 크기 배율을 가진 벡터 간 각도의 코사인임을 알 수 있따. 따라서 U와 V가 모두 단위 벡터일 경우 U V의 내적은 두 벡터 간 각도의 코사인이 된다.

만약 U . V = 0 라면 U 와 V는 수직이다.

만약 U . V > 0 라면 두 벡터 간의 각도 세타는 90도 보다 작다.

만약 U . V < 0 라먄 두 벡터 간의 각도 세타는 90도 보다 크다.

다음의 D3DX 함수를 이용하면 두 벡터 간의 내적을 계산할 수 있다.

FLOAT D3DXVecDot (
CONST D3DXVECTOR3 pV1; //왼쪽 피연산자
CONST D3DXVECTOR3 pV2; //오른쪽 피연산자
);

외적

벡터 수학이 정의하는 두번째 형식의 곱은 외적이다. 스칼라로 계산되는 내적과는 달리 외적은 다른 벡터로 계산되는데, u와 v 두 벡터의 외적을 수행하면 다른 벡터인 p를 얻으며, 이는 u와 v에 서로 직각을 이룬다. 즉,p는 u에 직각이며, p는 v에 직각이다. 외적은 다음과 같이 계산한다.

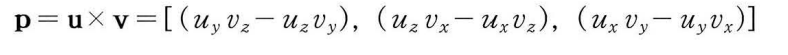
다음의 D3DX 함수를 이용하면 두 벡터 간의 외적을 계산할 수 있다.

D3DXVECTOR3 D3DXVec3Cross(
D3DXVECTOR3 pOut, //결과를 리턴한다.
const D3DVECTOR3 pV1 //왼쪽 피연산자
const D3DXVECTOR3 pV2 //오른쪽 피연산자
);

외적은 교환법칙 성립하지 않는다.

행렬

m x n 행렬은 m행과 n열을 가지는 일반적인 수 배열이다.
때로는 한 개의 행이나 열 만을 가지는 행렬이 있을 수 있는데, 이와 같은 행렬을 행 벡터 혹은 열 벡터라고 부른다.

행렬의 곱

행렬 곱AB를 얻기 위해서는 A의 열 수와 B의 행 수가 반드시 같아야 한다.

행렬의 곱은 일반적으로 교환적이지 않다.

항등 행렬

항등 행렬이라 불리는 특수한 행렬이 있다. 이는 중심 대각선을 제외하고 모든 항목이 0인 정방 행렬을 말하며, 중심 대각선의 항목들은 모두 1이다.

항등 행렬은 곱셈의 항등성을 가진다. 즉 곱셈의 교환법칙이 성립한다.

역행렬

행렬에는 나누기와 비교할 수있는 연산은 없지만 곱하기와 반대의 의미를 가지는 역 연산이 존재한다. 다음의 리스트는 역행렬에 대한 몇 가지 중요한 사항을 정리한 것이다.

• 정방 행렬만이 역행렬을 가질 수 있다. 즉, 역행렬에 대해 이야기할 때는 정방 행렬에 대해 이야기하는것과 같다.

• 모든 정방 행렬이 역행렬을 가지지는 않는다.

• 행렬과 역행렬을 곱하면 항등 행렬을 얻는다 : 행렬을 자신의 역행렬과 곱할때는 상호 교환적이다.

D3DXMATRIX* WINAPI D3DXMatrixInverse(

D3DXMATRIX *pOut, // 역행렬 결과

FLOAT *pDeterminant, //행렬식, 필요한 경우에 이용되며 그렇지 않으면 0전달

CONST D3DXMATRIX *pM // 뒤집을 행렬

);

행렬의 전치

행렬의 열과 행을 교환하면 행렬의 전치를 수행할수있다. 즉 mn행렬의 정치는 nm 행렬이다.

D3DX 행렬

Direct3D 애플리케이션을 프로그래밍할 때는 44 행렬과 14 행 벡터만을 이용한다. 두 가지 크기의 행렬만을 이용한다는 것은 다음과 같은 행렬 곱이 정의된다는 뜻이다.

• 벡터-행렬 곱. v가 14 행 벡터이고 T가 44 행렬이라면, 곱 vT가 정의되며, 그 결과는 1*4 행 벡터가 된다.

• 행렬-행렬 곱, T가 44 행렬이고 R이 44 행렬이라면, 곱 TR과 RT가 정의되며, 두 가지 모두 4*4 행렬이 된다. 행렬 곱은 상호 교환적이지 않으므로 곱 TR이 곱 RT와 같을 필요는 없다.

D3DX에서 1*4 행 벡터를 나타내기 위해,우리는 보통 D3DXVECTOR3와 D3DVECTOR4벡터 클래스를 이용한다. 물론, D3DXVECTOR3은 4개가 아닌 3개의 성분만을 가지고 있지만, 네번째 성분은 일반적으로 1이나 0으로 취급된다.

D3DX에서 4*4 행렬을 나타내는 데는 다음과 같이 정의된 D3DXMATRIX 클래스가 이용된다.

D3DMATRIX 클래스는 행렬의 동일함 확인이나 더하기,빼기,스칼라로 행렬 곱하기,형 변환, 그리고 무엇보다도 두 개의 D3DMATRIX를 곱하는 등의 유용한 연산자들을 다수 포함하고 있다.

D3DXMATRIX 클래스의 또 다른 주요 연산자로 괄호 연산자가 있으며, 이를 이용해 편리하게 행렬의 항목에 접근할 수 있다.

괄호 연산자를 이용할 때는 C의 배열과 마찬가지로 0으로 시작하는 인덱스를 지정한다는 것을 기억하자. 예를 들어, 행렬의 ij= 11 항목에 접근하기 위해서는 다음과 같은 코드를 사용한다.

D3DXMATRI M ;
M(0,0) = 5.0F; // ij = 11 항목을 5.0f로 지정한다.

D3DX 라이이브러리는 이외에도 유용한 함수들을 포함하고있다.

D3DXMATRIX D3DXMatrixIdentity(
D3DMATRIX pout //항등으로 지정될 행렬
);

D3DMATRIX D3DMatrixTranspose(
D3DXMATRIX pOut //결과로 얻어진 전치 행렬
CONST D3DMATRIX *pM //전치할 행렬
);

D3DXMATRIX WINAPI D3DXMatrixInverse(
D3DXMATRIX pOut, // 역행렬 결과
FLOAT pDeterminant, //행렬식, 필요한 경우에 이용되며 그렇지 않으면 0전달
CONST D3DXMATRIX pM // 뒤집을 행렬
);

기본적인 변환

Direct3D를 이용한 프로그래밍에서는 변환을 표현하기 위해 4*4 행렬을 이용하며, 기본적인 방식은 다음과 같다.

44 행렬 x의 각 항목에 특정한 변환을 나태는 값으로 채운 다음, 14 행 벡터 V의 열에 포인트의 좌표나 벡터를 넣는다.

44 행렬을 이용하는 것은 이 크기를 이용해 우리가 원하는 모든 변환을 표현할 수 있기 때문이다. 실제로 이동이나 투영 반사 등과 같이 33 행렬로는 표현할 수 없는 변환들이 있다.

앞서 우리는 14 행 벡터의 열에 포인트의 좌표나 벡터의 성분을 넣는다고 하였다. 하지만 포인트나 벡터는 3D가 아닌가! 14 행 벡터를 이용하는 이유는 무엇일까? 벡터-행렬 곱을 정의하기 위해서는 4ㅇD 행벡터에 3D 포인트/벡터를 보충해야 한다. 즉,13 행 벡터와 44 행렬의 곱은 정의할 수가 없다.

w성분을 1로지정하면 포인트 0으로 지정하면 벡터

때로는 행렬 변환 과정에서 벡터의 W성분을 바꾸어 0도아니고 1도아닐수도있다.

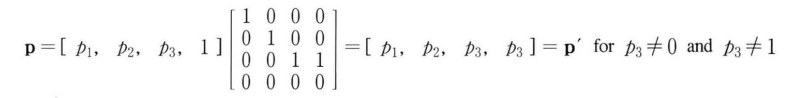
w = p3임을 지정, w는 0과1일 모두 아닐때 우리는 3-공강 내의 벡터와는 다른 동치 공간 내에 벡터를 가진 것이 된다. 이때 벡터의 각 성분을 w성분으로 나누면 동치 공간의 벡터를 3D로 매핑할 수 있다.
예를 들어, 동치 공간 내의 벡터 (x,y,z,w)fmf 3D벡터 x로 매핑하기 위해서는 다음과 같이 작성한다.

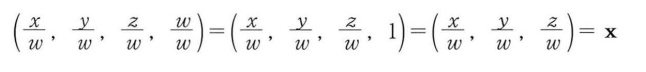
동치 공간에서 3D 공간으로의 매핑은 3D 그래픽 프로그래밍에서 원근 투영을 구현하는 데 이용된다.

-NOTE-
포인트 (X,Y,Z)를 (X,Y,Z,1)로 쓴다는 것은 기술적으로 4-공간 내의 4D 평면에 3D 공간을 묘사하는 것과 같다(3D 내의 평면이 2D 공간인 것처럼 4D 내의 평면은 3D 공간이다.)따라서 W를 다른 것을 ㅗ지정할 때는 W=1 평면을 떠나게 된다. 우리의 3D 공간과 대응되는 평면으로 돌아오기 위해서는 각 성분을 W로 나누어 3D 평면에 투영해야 한다.

이동행렬

(X,Y,Z,1) 벡터를 다음과 같은 행렬로 곱하면 X축으로 PX, Y축으로 PY, Z축으로 PZ단위 만큼 이동시킬 수 있다.

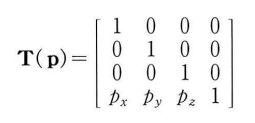
다음은 이동 행렬을 구성하느 D3DX 함수이다.

D3DMATRIX D3DXMatrixTranslation (
D3DXMATRIX pOut //결과
FLOAT X //X축으로 이동할 단위의 수
FLOAT Y //Y ""
FLOAT Z //Z ""
);

이동 벡터 P의 부호를 바꾸는 것으로 간단하게 이동 행렬의 역행렬을 얻을 수 있다.

회전행렬

다음의 행렬을 이용하면 X,Y,Z 축에서 벡터 라디안을 회전시킬 수 있다. 각도는 회전축을 내려다 볼 때 시계 방향으로 측정한다.

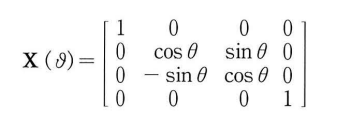
다음은 X축회전 행렬을 구성하는 D3DX 함수이다

D3DMATRIX D3DMatrixRotationX(
D3DMATRIX pOut // 결과
FLOAT Angle // 라디안으로 측정한 회전각
);

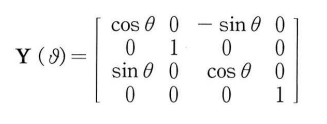
다음은 Y축회전 행렬을 구성하는 D3DX 함수이다

D3DMATRIX D3DMatrixRotationY(
D3DMATRIX pOut // 결과
FLOAT Angle // 라디안으로 측정한 회전각
);

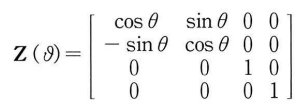
다음은 Y축회전 행렬을 구성하는 D3DX 함수이다

D3DMATRIX D3DMatrixRotationZ(
D3DMATRIX pOut // 결과
FLOAT Angle // 라디안으로 측정한 회전각
);

행렬 R의 역은 전치 R이다. 이와 같은 행렬은 직각이라 말할 수 있다.

크기 변형 행렬

다음의 행렬을 벡터와 곱하면 x축으로 qx단위만큼 y축으로 qy단위 만큼 z축으로 qz단위만큼 벡터의 크기를 변경할 수 있다.

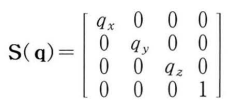
다음은 크기 변형 행렬을 구성하는 D3DX 함수이다.

D3DMATRIX D3DXMatrixScaling(
D3DMATRIX pOut, //결과
FLOAT SX //X축 크기 변형 단위
FLOAT SY //Y축 크기 변형 단위
FLOAT SZ //Z축 크기 변형 단위
);

크기 변형 행렬의 역은 각 크기 변형 인자의 역으로 얻어진다.

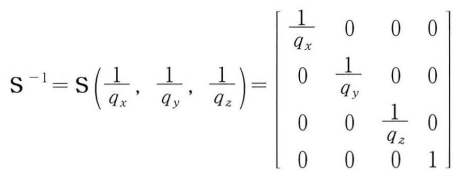
변환 조합하기

하나의 벡터에 일련의 변환을 적용해야 하는 경우가 많다. 예를 들ㅇ어 벡터의 배율을 변경하고 회전시킨 다음, 이를 원하는 우치로 이동하고자 한다면 어떻게 해야 할까?

크기 변형과 회전,이동을 위한 변환 순서를 차례를 적용하면 다음과 같은 결과를 얻는다.

행렬의 한 가지 중요한 이점은 행렬 곱을 이용하여 몇가지 변환을 하나의 행렬로 결합할 수 있다는 것이다. 여기에서 변환을 위해 곱한 순서는 최종적으로 적용되는 변환의 순서가 된다.

여러 개의 변환을 하나의 변환으로 결합하는 능력은 성능에도 영향을 준다. 다수의 벡터에 동일한 크기 변형,회전,이동 변환을 적용해야 한다고 가정해보자(3D 그래픽 에서는 흔한 작업이다). 하나의 행렬로 세 개의 변환을 한 번에 수행할 수 있다. 이와 같은 작업 방식은 벡터-행렬 곱 연산의 수를 획기적으로 줄여줄 수 있다.

벡터 변환을 위한 몇 가지 함수들

D3DX 라이브러리는 포인트와 벡터 변환을 위한 두 개의 함수를 제공한다. D3DXVec3TransformCoord 함수는 포인트를 변환하며, 벡터의 네번째 성분이 1로 인식된다고 가정한다.
D3DXVec3TransformNormal 함수는 벡터를 변환하며 벡터의 네번째 성분이 0으로 인식된다고 가정한다.

D3DVECTOR3 D3DVec3TransformCoord(
D3DVECTOR3 pOut //결과
CONST D3DVECTOR3 pV //변환할 포인트
CONST D3DMATRIX pM //변환 행렬
);

D3DVECTOR3 D3DVec3TransformNormal(
D3DVECTOR3 pOut //결과
CONST D3DVECTOR3 pV //변환할 벡터
CONST D3DMATRIX pM //변환 행렬
);

평면

평면은 하나의 벡터 n과 평면 상의 포인트 p0으로 표현된다. 벡터 n은 평면의 법선 벡터라고 부르며 평면과 수직을 이룬다.

n . (p - p0) = 0
: p0이 평면 상의 포인트일 때,(p - p0)으로 구성한 벡터가 평면의 법선 벡터와 직각일 경우, 포인트p 역시 평면 상에 위치한다.

특정 평면을 표현하는 데 있어 법선 n과 평면 상의 알려진 포인트 p0은 고정된다. 따라서 위의 식을 다음과 같이 작성하는 것이 일반적이다.

n . p +d =0

-NOTE-
평면의 법선 벡터 n이 단위 길이일 경우, d = -n . p0으로 원점에서 평면까지의 부호를 가진 가장 짧은 거리를 얻을 수 있다.

D3DXPLANE

코드에서 평면을 표현할 때는 법선 벡터 n과 상수 d를 보관하는 것으로 충분하며, (n,d)로 표기하는 4D벡터의 하나로 생각해도 된다. D3DX 라이브러리는 다음과 같은 구조체를 평면으로 표현하다.

a,b,c는 각각 평면의 법선 벡터 n의 성분이 되며,d는 위 식의 d이다.

포인트와 평면 공간 관계

n . p +d =0 식은 평면에서 포인트의 상대적 위치를 테스트하는 데 매우 유용하다. 예를 들어,평면 (n,d)가 있다고 할때,포인트 p가 평면과 어떤 관계에 있는지를 확인할 수 있다.

n . p +d =0 p는 평면과 공면에 있다.

n . p +d > 0 라면, p는 평면의 앞쪽 양의 절반 공간에 있다.

n . p +d < 0 라면, p는 평면의 뒤족 음의 절반 공간에 있다.

-NOTE-
만약 평면의 법선 벡터 n이 단위 길이라면, n . p +d로 평면에서 포인트 p까지의 부호를 가진 가장 짧은 거리를 얻을 수 있다.

다음의 D3DX 함수는 특정 평면과 포인트를 위한 n . p +d를 계산한다.

FLOAT D3DXPlanedDotCoord(
CONST D3DXPLANE pP //평면
CONST D3DXVECTOR3 pV //포인트
);

평면 구축

법선과 평면의 부호 거리를 곧바로 지정하는 방법 이외에도 이를 계산하는 두 가지 방법이 있다. 법선 N과 평면 상의 알려진 포인트 P0이있다고 하면, d성분은 다음과 같이 풀어낼 수 있다.
d = -n . p0

D3DX 라이브러리는 이 계산을 위해 다음의 함수를 제공한다.

D3DXPLANE D3DXPlaneFromPointNormal (
D3DXPLANE pOut, //결과
CONST D3DVECTOR3 pPoint //평면 상의 포인트
CONST D3DVECTOR3 pNormal //평면의 법선
);

평면을 구축하는 두번째 방법은 평면 상의 세 개의 포인트를 지정하는 것이다.

P0,P1,P2 포인트가 있다면 평면상의 두 개의 벡터를 구성할 수있다.

U = P1 - P0
V = P2 - P0
이제 평면상에 있는 두 벡터의 외적을 얻으면 평면의 법선이 계산된다. 왼손 엄지 손가락의 법칙을 기억하자

n = u * v (외적)

이제, -(n . p0) = d가 된다.

d3dx 라이브러리는 평면 상의 주어진 세 개의 포인트를 이용해 평면을 계산하는 다음과 같은 함수를 제공한다.

D3DXPLANE D3DXPlaneFromPoints(
D3DXPLANE pOut //결과
CONST D3DXVECTOR3 pV1 //평면상의 포인트1
CONST D3DXVECTOR3 pV2 //평면상의 포인트2
CONST D3DXVECTOR3* pV3 //평면상의 포인트3
);

평면 정규화

때로는 평면의 법선 벡터를 정규화해야 하는 상황이 있다. 법선 벡터의 길이가 상수 d에 영향을 주기 때문에,법선 벡터를 정규화하면 d역시 다시 계산해야한다.

다음은 평면의 법선 벡터를 정규화하기 위해 사용되는 D3DX 함수이다.

D3DXPLANE D3DXPlaneNormalize(
D3DXPLANE pOut //정규화된 결과 평면
CONST D3DXPLANE *pP //입력 평면
);

편명 변환

평면 (n,d)를 4D 벡터로 취급하고 원한는 변환 행렬의 역-전치와 곱함으로서 평면을 변환할수 있음을 보여주었다. 평면의 법선 벡터는 반드시 먼저 정규화되어야 한다는 데 주의하자.

이를 위해, 다음과 같은 D3DX 함수가 사용된다.
D3DXPLANE D3DXPlaneTransform(
D3DXPLANE pOut //결과
CONST D3DXPLANE pP //입력 평면
CONST D3DXMATRIX pM //변환 행렬
);

평면에서 특정 포인트와 가장 가까운 포인트

공간에 하나의 포인트 p를 가지고 있고 p와 가장 가까운 평면(n,d) 상의 포인트 q를 찾으려 한다고 가정해보자. 여기에서는 평면의 법선 벡터가 단위 길이라고 가정하며, 이러한 가정은 문제를 조금이나마 단순하게해준다.

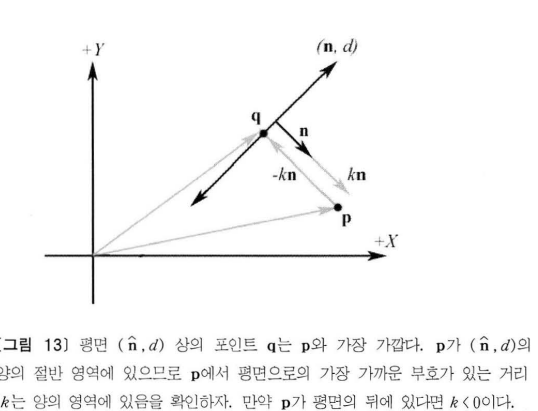
[그림 13] d에서 q= p + -kn이며, k는 p에서 평면으로의 부호가 있는 가장 짧은 거리이고,포인트 p와 q사이의 가장 짧은 부호가 있는 거리이기도 하다는 것을 알 수 있다. 평면의 법선 벡터 n이 단위 길이일 경우 n . p + d로 평면과 포인트 p간의 가장 짧은 부호가 있는 거리를 얻을 수 있다는 것을 기억하자.

광선

우리가 개발하는 게임 내의 플레이어가 걷는 도중에 적에게 총을 발사한다고 가정해보자. 특정 위치에서 어떤 방향으로 발사된 총알이 타겟에 맞았는지를 확인하는 방법은 무엇일까? 한 가지 방법은 총알을 모델링하고 적을 경계 구체로 모델링하는 것이다(경계 구체는 물체의 외각을 단단하게 포함하는 구체이며 물체의 대력적 부피를 나타낼 수 있다.)

관점과 방향을 이용하면 광선을 표현할 수 있다. 광선의 매개 변수 표시 방정식은 다음과 같다.

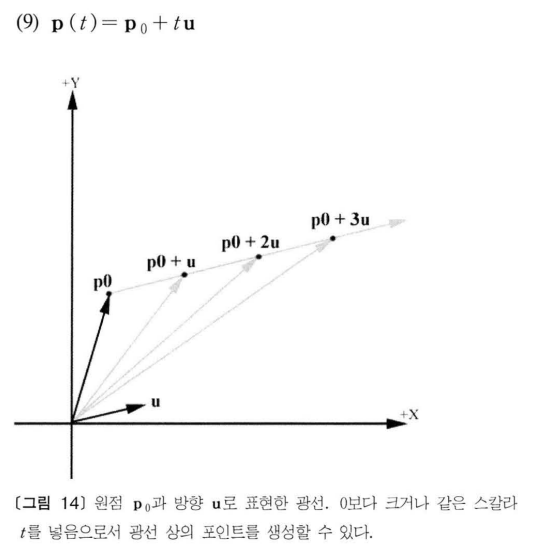
p0 : 광선의 원점
u : 광선의 방향
t : 매개 변수

t에 다른 값을 넣으면 광선 상의 다른 포인트를 계산할 수 있다. 매개 변수 t는 반드시 [0,무한) 범위 내에 있어야 하며, 0보다 작은 값을 이용하면 광선 뒤쪽에 포인트가 만들어짐.

광선 평면 교차

광선 p와 평면 n .p +d =0가 있다고 할때,광선이 평면과 교차하는지의 여부와 교차점의 포인트를 구하기 위해서는 평면 방적시에 광선을 넣고 평면 방정식을 만족시키는 매개 변수 t를 풀어내면된다.

만약 t가 범위 [0,무한) 내에 있지 않으면, 광선은 평면과 교차하지 않는다.

만약 범위 내에있다면 평면 방정식을 만족시키는 매개 변수를 광선 방정식에 넣어 교차점을 얻을 수 있다.

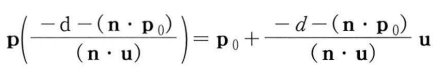
요약

*크기와 방향을 가지는 물리학적 양을 수학적으로 모델링하기 위해서는 벡터를 이용한다. 기하학적으로 벡터는 방향을 가진 선분이라고 말할 수 있으며, 좌표 시스템의 원점에 꼬리가 일치하도록 벡터를 표준 위치로 이동시킨 다음, 이렇게 표준 위치에 옮긴 벡터의 머리 좌표를 표시하면 대수학적으로 벡터를 표기할 수 있다.

변환을 나타내는 데는 44 행렬을 이용하며, 포인트와 벡터를 나타내는 데는 14 동치 행렬을 이용한다. 14 행 벡터와 44 변환 행렬의 벡터-행렬 곱은 새로이 변환된 14 행 벡터를 결과로 만들어낸다. 행렬-행렬 곱을 통해 여러 개의 변환 행렬을 하나의 변환 행렬로 결합하는 것이 가능하다.

*벡터와 포인트를 나타내는 데는 모두 4D 동치 벡터를 이용한다. 벡터를 표기할 때는 w성분에 0을 지정하며, 포인트를 표기할 때는 w성분에 1을 지정한다. 만약 w가 0,1이 아닐 때는 각 성분을 w로 나누어 3-공간으로 매핑할 수 있는 동치 공간 내의 벡터 (x,y,z,w)를 가진 것이다.

*평면은 3D 공간을 두 개의 부분으로 나눈다: 양의 절반 공간은 평면의 앞쪽에 위치하며, 음의 절반 공간은 평면의 뒤쪽에 위치한다. 평면은 평면과 상대적인 포인트의 위치를 테스트하는 데 유용하다(다른 말로 하면,포인트가 특정 평면의 어떤 절반 공간에 있는지 알 수 있다).

• 광선은 원점과 방향 벡터를 이용해 매개적으로 표현할 수 있다. 광선은 빛 줄기나 총일이나 로켓과 같이 선형 경로를 따르는 발사체를 모델링하는 데 상당히 유용하다.