행렬(matrix)은 벡터를 원소로 가지는 2차원 배열입니다.
벡터가 공간에서 한 점을 의미한다면 행렬은 여러 점들을 나타냅니다.
행렬끼리 덧셈
같은 모양을 가지면 덧셈, 뺄셈을 계산할 수 있습니다.
행렬끼리 곱셈
행렬 곱셈은 2가지로 나뉩니다.
- Element Wise Product : 요소 끼리의 곱셈 (성분곱)
- Dot Product : i 번째 행벡터와 j 번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산합니다. (여기서 말하는 내적은 수학에서 말하는 내적과는 다르므로 주의!)
보통 Matrix Multiplication 은 Dot Product 를 의미합니다. 넘파이의 np.inner() 함수를 사용해서 행렬곱을 계산할 수 있습니다.
임성빈 교수님의 Lecture Note에서는 행렬을 이해하는 새로운 방법에 대해 소개하고 있습니다.
행렬을 벡터공간에서 사용되는 연산자(Operator)로 이해하고, 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다고 설명합니다.

행렬곱을 통해 패턴을 추출할 수 있고 데이터를 압축할 수도 있다.
역행렬
어떤 행렬 A의 연산을 거꾸로 되돌리는 행렬을 역행렬(inverse matrix)이라 부른다. 역행렬은 행과 열의 숫자가 같고 행렬식(determinant)이 0이 아닌 경우에만 계산할 수 있다.
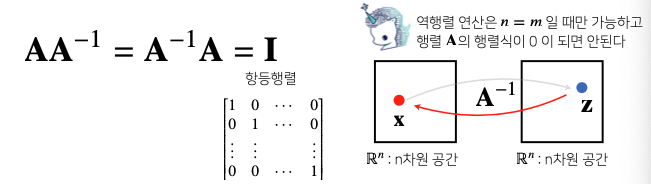
만약 역행렬을 계산할 수 없다면 유사역행렬(pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose) 역행렬을 이용한다.

