Table of Contents
- 미분이란?
- 미분은 어디에 쓸까?
- 변수가 벡터라면?
미분이란?
미분(differentiation)은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에서 제일 많이 사용되는 기법이다.
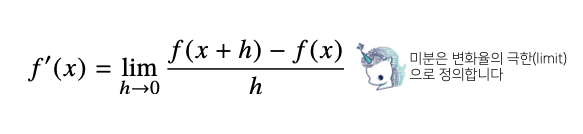
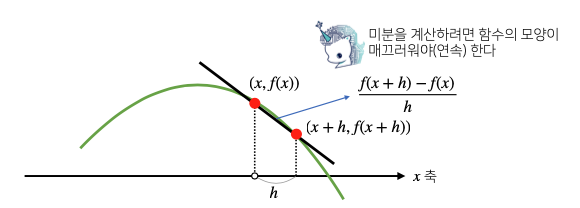
미분은 함수 f 의 주어진 점 (x, f(x)) 에서의 접선의 기울기 를 구한다. 미분이 가능하려면 연속함수 모양이어야 한다.
미분은 어디에 쓸까?
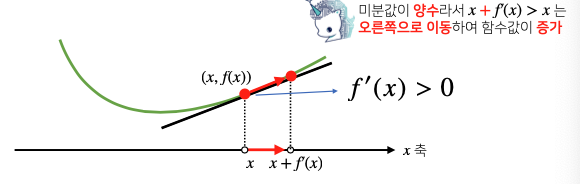
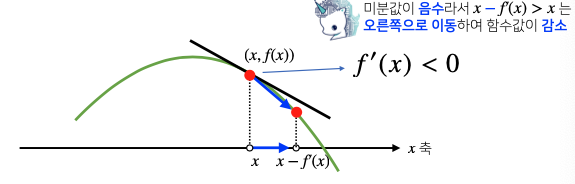
한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수값이 증가 또는 감소 하는지 알 수 있다.
증가시키고 싶다면 미분값을 더하고
감소시키고 싶으면 미분값을 빼면 된다.
미분값을 더하면 경사상승법(gradient ascent) 라 하며 극대값 의 위치를 구할 때 사용한다. 목적함수를 최대화 할때 사용한다.
미분값을 빼면 경사하강법(gradient descent) 라 하며 함수의 극소값 의 위치를 구할 때 사용한다.
미분값을 더하거나 빼면서 경사하강/상승 방법을 사용하면 어느 순간 극값에 도달하여 움직임을 멈추게 된다. 미분값이 0에 가까워 지면 더하거나 빼도 이동을 하지 않는다.
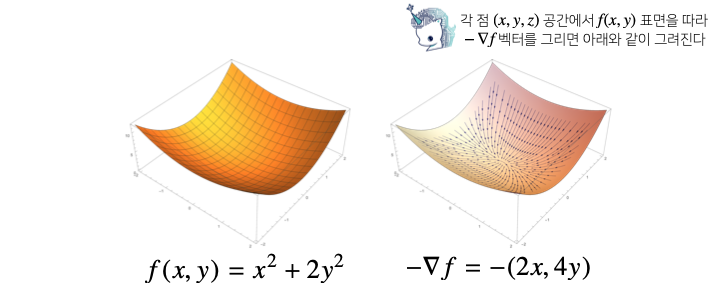
변수가 벡터라면?
벡터가 입력인 다변수 함수의 경우 편미분(partial differentiation)을 사용한다.
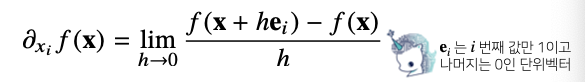
각 변수 별로 편미분을 계산한 그레디언트 벡터를 이용하여 경사하강/경사상승법에 사용할 수 있다.
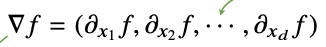
앞에 보이는 기호는 "nabla" 라 부른다.
앞서 사용한 미분값인 f'(x) 대신 그레디언트 벡터를 사용하여 변수 x = (x1, x2, .... , xd) 를 동시에 업데이트 가능하다.