Intro
나는 수학이 좋았다. 수학과에 대한 미련을 접고 난 후 갈 곳을 잃었다. 그 당시 재수학원 원장님께 상담결과 ‘너는 프로그래밍이랑 잘 맞을 것 같은데?’ 이 한마디에 그래서 20살까지 독수리타법을 치던 내가 아무것도 모른채 컴공과를 가게되었다.(너무 너무 감사합니다🙏)
하지만 내가 생각하던 프로그래밍과 학교에서 배우는 수업은 조금 달랐고 생각보다 흥미가 있지 않았다. 코딩을 하며 흥미를 느낀 것은 의외로 FE개발을 접해보면서였고, 여러 고민끝에 FE로 진로를 정하게 되었다.
하지만 FE 엔지니어가 되어야겠다 생각을 하며 공부를 하였지만 수학 관련된 생각을 한 적이 없었다.
다시 나를 돌아보니 내가 수학을 좋아하는 이유는 ‘증명’ 때문이었다.
가능한 모든 케이스 검증을 통한 증명이 아닌, 이미 증명된 공리를 이용한 새로운 증명 때문이었다.
이를 프로그래밍에 대입해보면 선배들의 경험적으로 발생하는 케이스들을 체크한 후 가장 좋은 방법이되었던 best practice가 아닌
이미 테스트 완료된 된 것들을 이용해서 새로운 것을 만들면 테스트 통과를 한 효과를 지닌다는 것이고, 이는 아주 명쾌하게 다가왔다. (이는 순수함수로 인해 불변성이 보장되기 때문에 발생하는 부수효과라고 생각한다.)
구글의 정보의 늪에서 허우적거리다가 함수형 프로그래밍을 대수적 관점으로 설명해준 글을 보게되었고 배워보고 싶은 욕망이 아주 강하게 들었다.
프로그래밍이 어려운 이유는 예상치 못한 에러를 마주하기 때문이라고 생각한다.
내가 수학을 좋아했던 이유, 프로그래밍을 하면서 마음 한켠에 찝찝함이 남아있던 이유를 함수형 프로그래밍 패러다임을 공부해보며 답을 찾을 수 있을 것 같다는 기대감이 들었다.
정리
아래내용은 아주아주아주 얕은 내 지식으로 여러 글들을 읽으며 정리해본 내용이다.
아주 얕은 지식으로 작성된 글이며 반박 시 여러분 말이 95%확률로 맞으며 언제든지 환영합니다.
객체지향 프로그래밍과 함수형 프로그래밍의 가장 큰 차이는 무엇이 중심인가 라고 생각한다.
- 객체지향 : 객체가 중심
- 함수형 : 행동이 중심
내가 생각한 함수형 프로그래밍의 핵심은 작게 나누고 작은 단위가 증명되었다면 그것들을 이용해 합성한 것도 보장된다는 것이다. (지지고 볶으며 패배한 아토믹 디자인 패턴과도 결이 맞는 느낌쓰?)
- A, B함수가 테스트를 성공한다면(증명이 되었다면)
- A와 B를 이용해서 만든 C함수의 성공이 보장된다 (A, B는 C에게 공리가 된다.)
이다.
이를 통해 구현된 프로그램은 예외 케이스를 만들지 않고 에러가 사라질 것이라고 생각했다.(물론 100%에러가 없다는건 말이 안되겠지만..)
물론 모든 경우의 함수를 합칠 수 있는 건 아니다. 함수를 합성하기 위해서는 정의역(x)값과 공역(y)값이 일치해야 한다.
이는 수학에서의 합성함수와 동일한 이론이다.

수학에서의 정의역, 공역의 범위로 될 수 있는 것들은 정수, 유리수, 무리수, 허수 등 의 범주가 있다.
이를 프로그래밍 세계로 가져와보면 정의역 공역의 범위로 될 수 있는 것이 바로 타입이다.
이게 프로그래밍을 대수관점으로 바라볼 수 있게되는 핵심이라고 생각하다.
타입과 수학과의 표기 차이를 보면
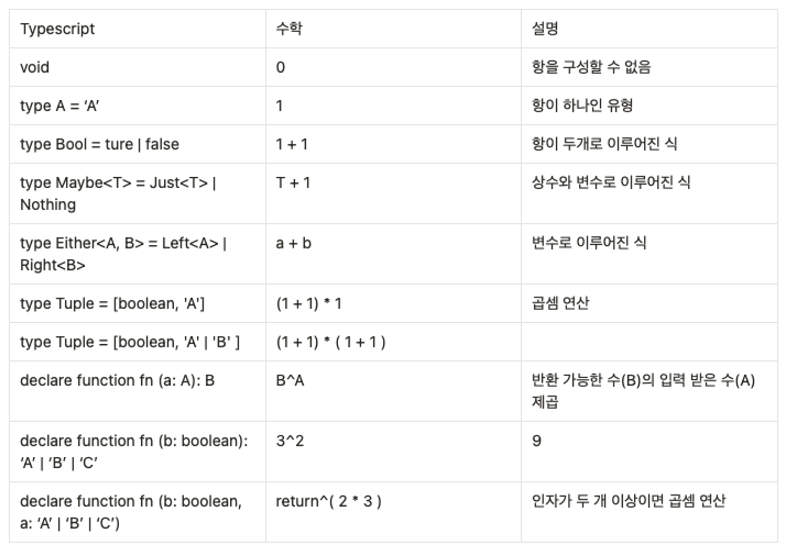
이렇게 나타내진다.
이런 제약조건들로 모든 것을 순수함수의 합성을 만들 수 있는 것은 아니다. 또한 이러한 순수 함수의 합성들로 구성되어있다고 해도 모든 경우를 커버할 수 없다.
그래서 펑터, 모다드, 어플리케이티드 펑더 등의 개념이 필요해진것이다.
어떻게 하면 안전하게 함수를 합성할 수 있을까? 의 글에서의 예시를 빌리자면
function getFirstLetter (s: string): string {
return s[0];
}이러한 순수함수가 있을 때
getStringLength(getFirstLetter(''));처럼 빈문자열을 넣어준다면 에러가 나게되고 이것도 하나의 사이트 이펙트이다 라고 설명하고 있다.
사실 getFirstLetter 의 공역은 string이 아니라 string | undefined 이기 때문이라고 설명해주며 이와 같은 경우를 위해
function getFirstLetter (s: string): string|undefined {
return s[0];
}
function getStringLength (s: string|undefined): number {
if (!s) {
return -1;
}
return s.length;
}
// 위의 방식을 우아하게 하면
function safety <T, U>(x: T|undefined, fn: (x: T) => U) {
return x ? fn(x) : x;
}
safety<string, number>(getFirstLetter('Hi'), getStringLength);
safety<string, number>(getFirstLetter(''), getStringLength);처럼 예외 처리를 통해 해결할 수 있다고 설명해주었다.
이글을 보고 이런 생각이 들었다.
수학에서의 함수를 생각해보면 정의역에 들어가는 값에 제한이 붙는다.
f(x) = 2/x 이런 함수를 생각해보면 뒤에 항상 (단, x는 0이 아님)
빈문자열이 들어가는 경우는 ‘단, x는 0이 아님’ 과 같은 경우 아닐까? 이런 조건이 있는 경우 함수 내부에서 판단해주는 것이 아닌 함수에 값을 넣는 내가 0이 아닐 때만 넣어줘야한다.
이를 프로그래밍 세계에 대입해보면 함수 내부에서 처리해주는게 아닌 사용하는 곳에서 이런 경우를 배제하고 보내주는게 맞지 않을까? 생각이 들었다.
하지만 이는 명령형 프로그래밍에 가깝고 함수형 프로그래밍의 상위 개념인 선언형이라는 맞지 않다는 생각이 들었다…
그리고 펑터 라는 개념을 설명해주셨다. (슈뢰딩거의 고양이 느낌 같기도 하고..?)
내가 이해하기로는 순수함수를 감싸 예외처리를 해주는 역할이라고 까지만 이해가 되었다,,, 어려워ㅠ
찍먹 후기
순수함수는 그냥 우리가 수학에서 배우던 수학적인 함수이다.
즉, 수학에서의 함수를 프로그래밍에 그대로 적용하면 순수한 함수의 특성인 “함수의 결과는 함수의 인자에만 영향을 받는다”라는 조건과 “함수 외부의 상태를 변경하거나 영향을 받아선 안된다”라는 조건이 자연스럽게 충족되는 것이다.
⇒ 불변성
이 두문장에 가장 함수형 프로그램을 공부하는데 가장 잘 와닿았다.
함수형 프로그래밍의 장점은 순수함수를 사용함으로 따라오는 것들이고, 순수함수의 장점은 불변성이라고 생각한다.
그러면 항상 함수형 프로그래밍이 OOP보다 좋은것이냐? 이건 절대 아니다.
순수함수에서 불변성이 지키기 위해서는 비용이든다.
Array, Object같은 자료형은 태생 부터가 상태값 변경을 위해 생성되었다. 이런 태생을 거스르고 불변성을 유지하기 위해서는 비용을 내야한다. 기존의 상태값을 복사해서 변경하는 것이다.
만약 기존의 상태값에 많은 정보가 담겨져 있다면 불변성을 유지하는 비용으로 상태를 복사하는 값을 많이 치뤄야 한다. 이는 퍼포먼스가 중요한 서비스에서는 맞지 않는 방법이다.
데브코스 1차 멘토님의 말씀이 생각났다.
대부분 많은경우에서 퍼포먼스보다 중요시되는 것은 가독성과 일관성이다.
비슷한 논리로 발전된 하드웨어 덕분에 퍼포먼스에대한 고민을 내려놓고 유지보수 측면에서본다면 함수형 프로그래밍이 두각을 나타내는 부분이 분명있을 꺼라고 생각한다.
이번에 함수형 프로그래밍을 공부해 보면서 스스로 목표는 함수형 프로그래밍의 패러다임을 이해하고 비용을 치루면서라도 불변성이 더 중요한 부분을 리팩토링해보는 것을 목표로 정했다.
데나무숲 v2 리팩토링 가즈아ㅏ
참고
대수로 다룬 함수형 프로그래밍 : https://moonsupport.oopy.io/post/30
함수형 사고 : https://moonsupport.oopy.io/post/30
순수 함수 : https://evan-moon.github.io/2019/12/29/about-pure-functions/
불변성 : https://evan-moon.github.io/2020/01/05/what-is-immutable/
안전한 합성 함수 : https://evan-moon.github.io/2020/01/27/safety-function-composition/
