개요
DFS / BFS 는 탐색 알고리즘으로써 역할을 하는데, 여기서 탐색이란 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정 이다. 이들을 구현하기 위해서는 스택과 큐라는 자료구조를 활용한다.
자료구조란 데이터를 표현하고 관리하고 처리하기 위한 구조 를 의미한다
DFS
DFS는 Depth-First Search, 깊이 우선 탐색이라고도 부르며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘 이다. 그래프란 노드(정점) 과 간선으로 표현되며, 그래프를 탐색한다는 것은 하나의 노드를 시작으로 다수의 노드를 방문하는 것을 말한다.
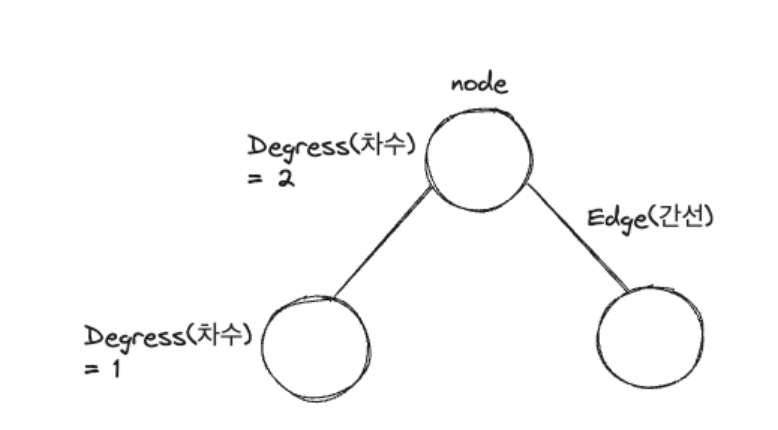
그림 출처: 사이트
DFS 동작 과정
1. 탐색 시작 노드를 스택에 삽입하고 방문 처리
2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리를 한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
3. 2번 과정을 더 이상 수행할 수 없을 때까지 반복한다.
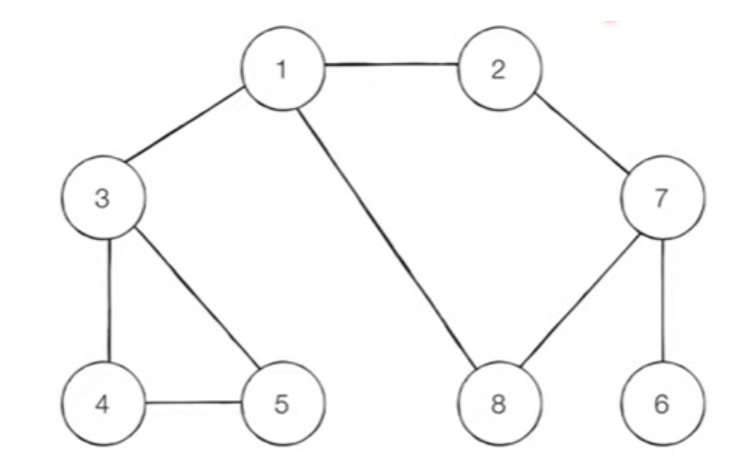
- 관행적으로 번호가 낮은 순서대로 처리하도록 구현하기에 이에 따라 순차적으로 dfs 를 적용해보도록 하자.
- 1번 노드를 탐색 시작 노드로 가정하고, 이를 스택에 삽입한 후 방문 처리를 한다. (스택:
1) - 1번 노드와 연결된 노드는 2, 3 노드인데 숫자가 낮은 2부터 스택에 삽입하고, 방문 처리를 한다. - 1번 노드를 탐색 시작 노드로 가정하고, 이를 스택에 삽입한 후 방문 처리를 한다. (스택:
1, 2) - 다음은 7을 스택에 넣고 방문 처리 (스택:
1, 2, 7) - 다음은 6을 스택에 넣고 방문 처리 (스택:
1, 2, 7, 6) - 그리고 나서 6과 연결된 노드는 없으므로 스택에서 6번 노드를 꺼낸다. (스택:
1, 2, 7) - 위의 과정을 반복하면 결과적으로
1 2 7 6 8 3 4 5순서대로 탐색했다.(= 스택에 들어갔다)
DFS 구현
DFS는 스택을 이용하는 알고리즘이기 때문에, 재귀 함수를 이용하여 구현할 수 있다.
def dfs(graph, v, visited):
visited[v] = True
print(v, end=' ')
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visited = [False] * 9
dfs(graph, 1, visited)재귀 함수의 수행은 스택 자료구조를 이용한다. 재귀 함수는 가장 마지막에 호출한 함수가 먼저 수행을 끝내야 그 앞의 함수 호출이 종료된다. 즉, 컴퓨터 구조 측면에서 연속해서 호출되는 함수는 메인 메모리의 스택 공간에 적재되므로 재귀함수는 스택 자료구조와 내부적으로 동일하다.
BFS
BFS는 너비 우선 탐색 이라는 의미를 가진다. 쉽게 말해 가까운 노드부터 탐색하는 알고리즘이다. DFS는 최대한 멀리 있는 노드를 우선적으로 탐색하는 방식으로 동작한다. 하지만 BFS는 반대이다. 참고로 BFS를 구현하기 위해서는 큐를 사용한다.
알고리즘 동작 순서
1. 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
2. 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리를 한다.
3. 2번 과정을 더 이상 수행할 수 없을 때까지 반복한다.
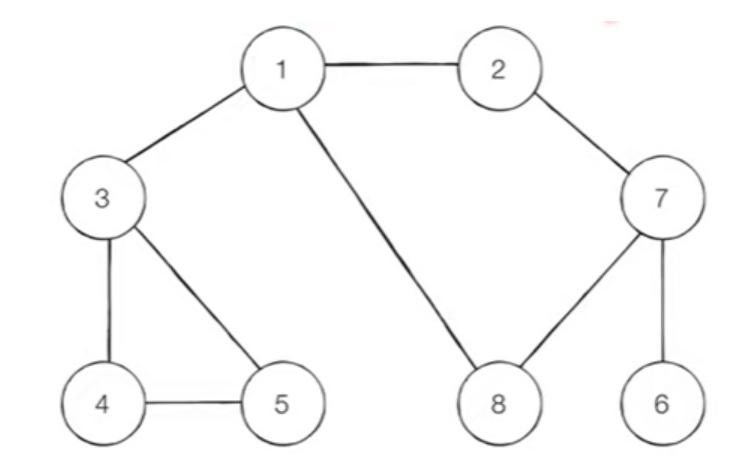
- 1번을 큐에 삽입한다. (큐:
1) - 1번을 큐에서 꺼내고, 1번과 인접한 노드 2, 3, 8을 순서대로 큐에 삽입한다. (큐:
2, 3, 8) - 2번을 큐에서 꺼내고, 인접한 7번 노드를 큐에 삽입한다 (큐:
3, 8, 7) - 3번을 큐에서 꺼내고, 인접한 4, 5번 노드를 큐에 삽입한다 (큐:
8, 7, 4, 5) - 8번을 큐에서 꺼낸다. 이때 8번과 인접한 노드는 더이상 없으므로 패스
- 이 과정을 반복하면
1 2 3 8 7 4 5 6순서대로 노드를 탐색한다. (= 큐에 들어간 순서)
BFS 구현
앞서 말했다시피 BFS는 큐를 이용해서 구현한다
from collections import deque
def bfs(graph, visited):
start = 1
visited[start] = True
q = deque([start])
while q:
v = q.popleft()
print(v, end=' ')
for i in graph[v]:
if not visited[i]:
q.append(i)
visited[i] = True
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visited = [False] * 9
bfs(graph, visited)시간 복잡도
두 시간복잡도는 모두 O(N) 이다. 왜냐하면 두 알고리즘 모두 한번 방문한 곳은 다시 방문하지 않기 때문에 노드의 수만큼 시간 복잡도가 나오게 된다.
참고) 그래프 표현 방식
- 인접 행렬: 2차원 배열로 그래프의 연결 관계를 표현하는 방식
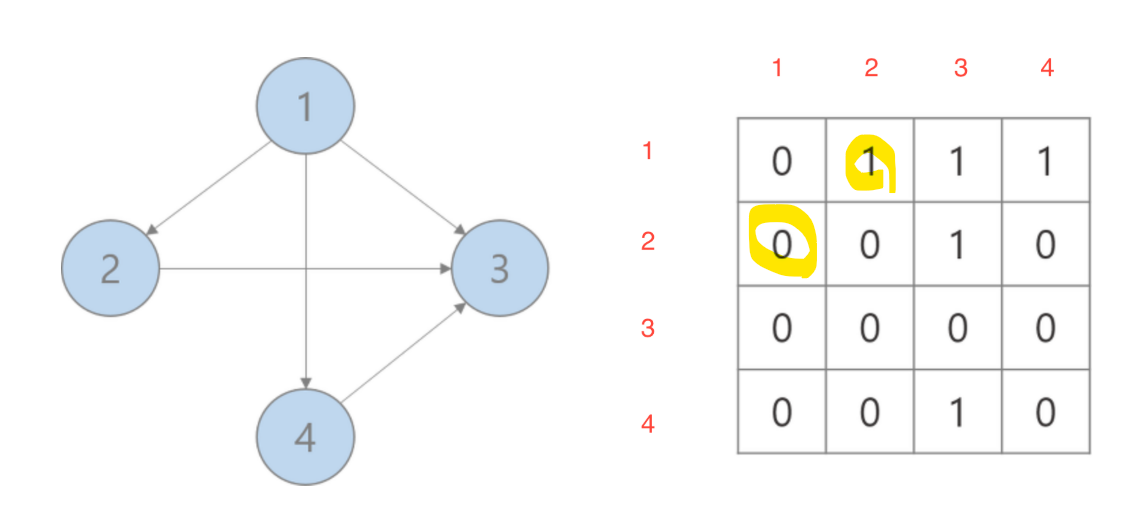
- graph[1][2]의 값이 1로 표현한 것은 1의 노드가 2의 노드를 가르킨다는 것이다. 다시 말해 1번 노드를 통해 2번 노드로 접근할 수 있다.
- graph[2][1]의 값이 0으로 표현된 것은 2의 노드가 1의 노드로 접근을 할 수 없다는 것이다. (0이 아닌 무한으로 표현하기도 함)
- 인접 리스트: 리스트로 그래프의 연결 관계를 표현하는 방식
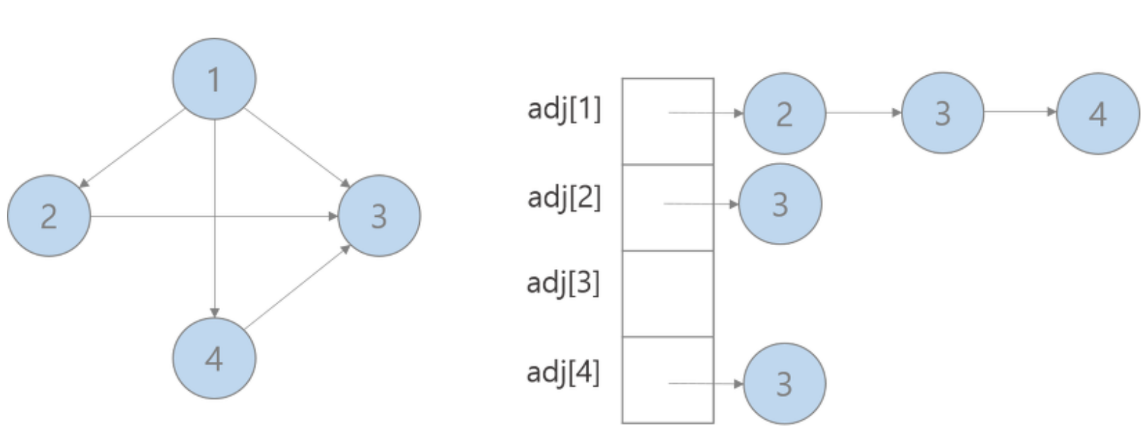
- 인접 리스트에서는 하나의 노드를 기준으로 자기 자신과 (직접적으로) 연결되어 있는 모든 간선 정보를 저장한다.
- 위의 그림에서는 다음과 같이 저장된다.
[[(1, 2), (1, 3), (1,4)], [(2, 3)], [], [(4, 3)]]
