알고리즘
1.그리디 알고리즘

그리디 알고리즘은 어떠한 문제가 있을 때 탐욕적으로 문제를 푸는 알고리즘이다. 이때 탐욕적이라는 말은 현재 상황에서 지금 당장 좋은 것만 고르는 방법을 의미한다. 즉, 현재의 선택이 나중에 미칠 영향에 대해서는 고려하지 않는다.따라서 그리디 문제를 해결하기 위해서는 단
2.DFS / BFS
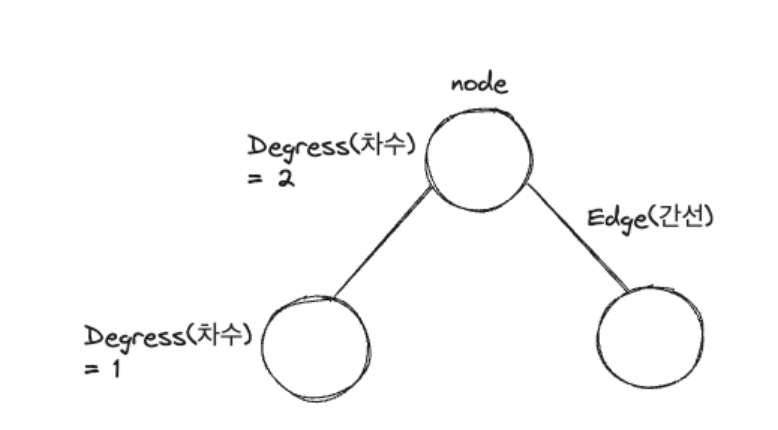
DFS / BFS 는 탐색 알고리즘으로써 역할을 하는데, 여기서 탐색이란 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정 이다. 이들을 구현하기 위해서는 스택과 큐라는 자료구조를 활용한다.자료구조란 데이터를 표현하고 관리하고 처리하기 위한 구조 를 의미한다DFS는
3.정렬 알고리즘

정렬이란 데이터를 특정한 기준에 따라 순서대로 나열 하는 것이다. 이러한 정렬은 이진 탐색의 필수 조건이기도 하다. 정렬 알고리즘은 다양한데, 그중에서 선택, 삽입, 퀵, 계수 정렬에 대해서 알아보도록 하자.데이터가 무작위로 여러개 있을 때, 이 중에서 가장 작은 데이
4.이진 탐색
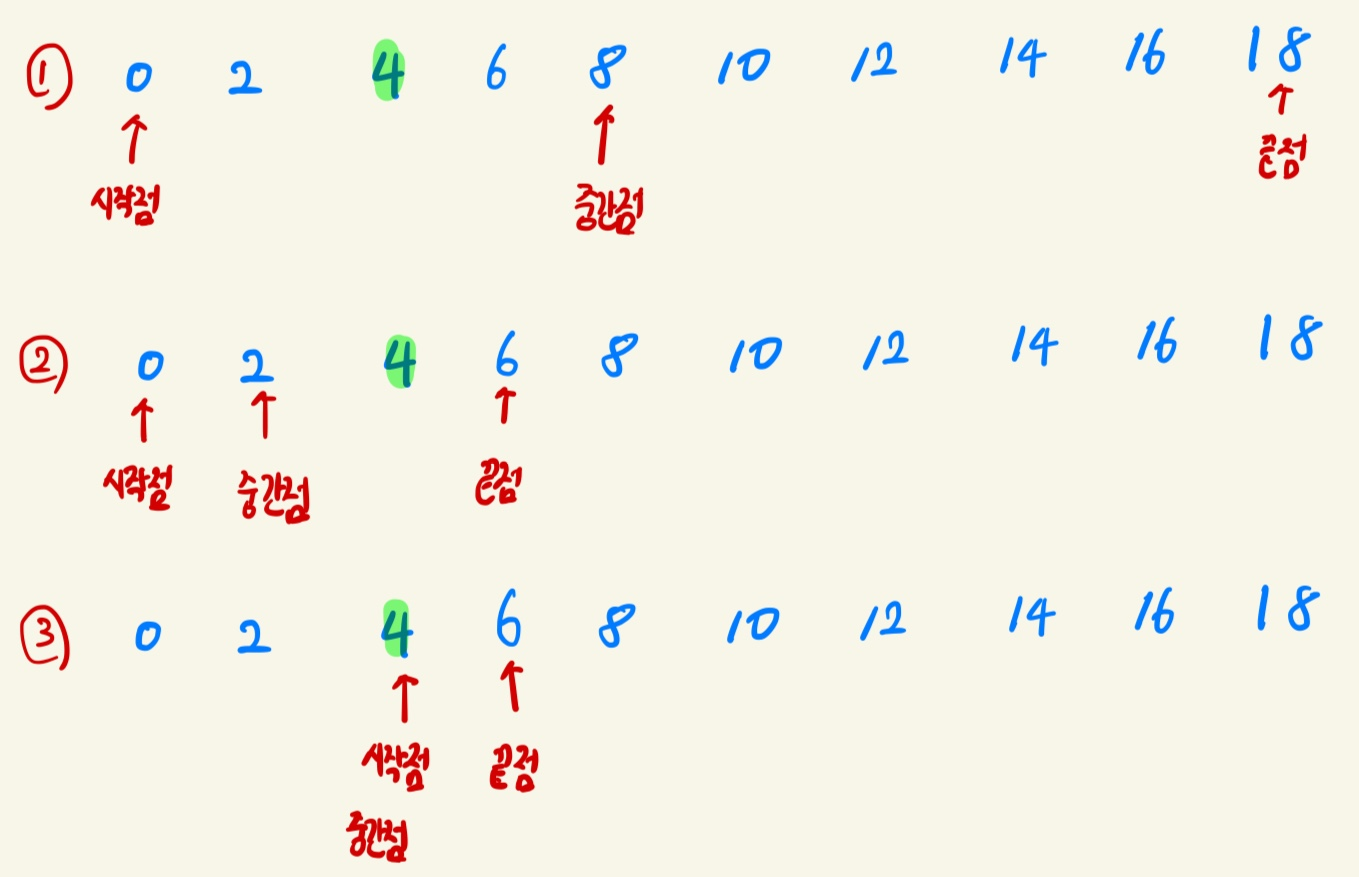
이진 탐색은 배열 내부의 데이터가 정렬되어 있어야만 사용할 수 있는 알고리즘이다. 이는 위치를 나타내는 변수 3개를 사용하는데 탐색하고자 하는 범위의 시작점, 끝점, 중간점이다. 찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾는게
5.다이나믹 프로그래밍
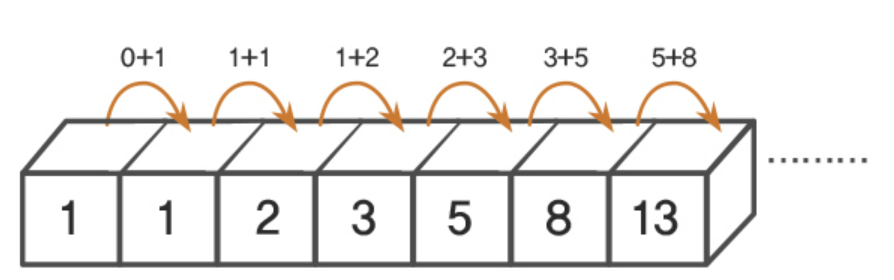
컴퓨터를 활용해도 해결하기 어려운 문제는 무엇일까? 최적의 해를 구하기에 시간이 매우 많이 필요하거나 메모리 공간이 매우 많이 필요한 문제 등이 컴퓨터로도 해결하기 어려운 문제이다. 따라서 우리는 메모리 공간을 약간 더 사용하여 연산 속도를 비약적으로 증가시키는 다이나
6.최단거리
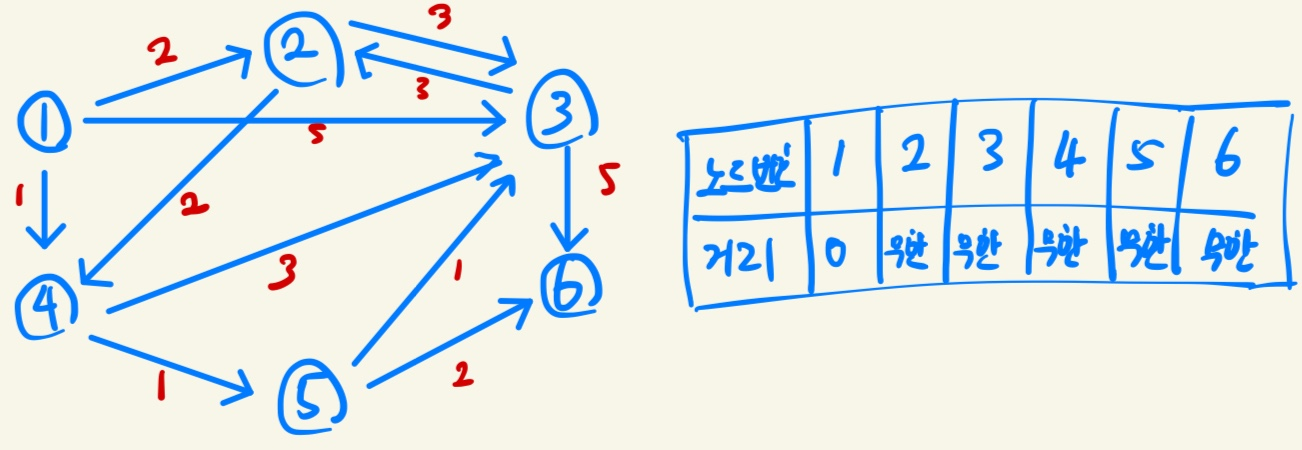
최단거리 알고리즘은 말 그대로 가장 짧은 경로를 찾는 알고리즘이다. 최단거리 알고리즘에는 한 지점에서 다른 특정 지점까지의 최단 경롤르 구해야 하는 경우 (다익스트라) & 모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 하는 경우(플로이드 워셜) 등이 있다
7.서로소 집합 & 사이클 판별 알고리즘
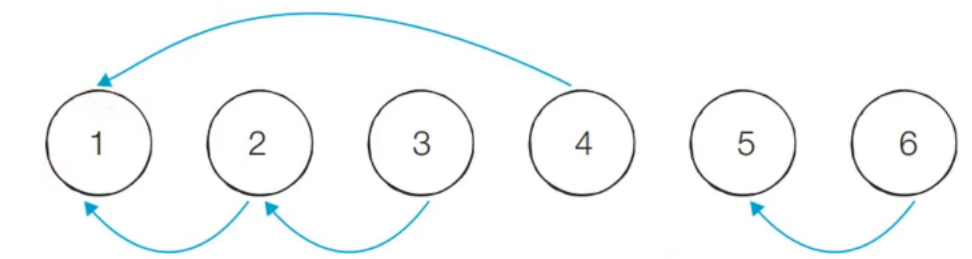
그래프란 노드와 노드 사이에 연결된 간선의 정보를 가지고 있는 자료구조를 의미한다. 예를 들어 여러 개의 도시가 연결되어 있다 와 같은 내용은 그래프 알고리즘을 일 수도 있다. 이러한 그래프 알고리즘의 유형으로는 dfs/bfs 최단 경로 크루스칼 알고리즘 위상 정렬 알
8.그래프: 크루스칼 알고리즘
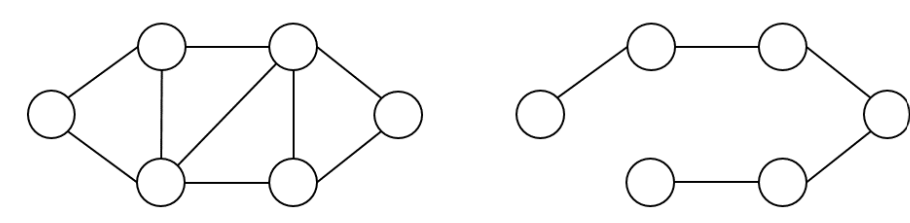
그래프란 노드와 노드 사이에 연결된 간선의 정보를 가지고 있는 자료구조를 의미한다. 예를 들어 여러 개의 도시가 연결되어 있다 와 같은 내용은 그래프 알고리즘을 일 수도 있다. 이러한 그래프 알고리즘의 유형으로는 dfs/bfs 최단 경로 크루스칼 알고리즘 위상 정렬 알
9.그래프: 위상 정렬
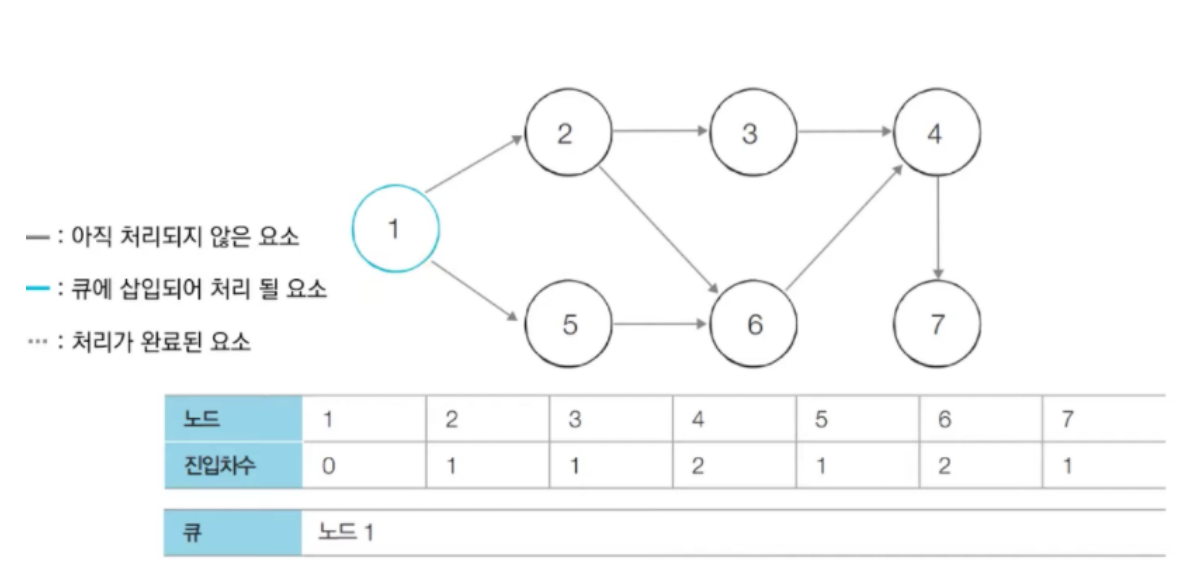
위상정렬은 정렬 알고리즘의 일종이다. 이는 순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용할 수 있는 알고리즘이다. 조금더 구체적으로 위상 정렬은 방향 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열하는 것이다. 예시로는 선수과목이 있다.
10.소수의 판별
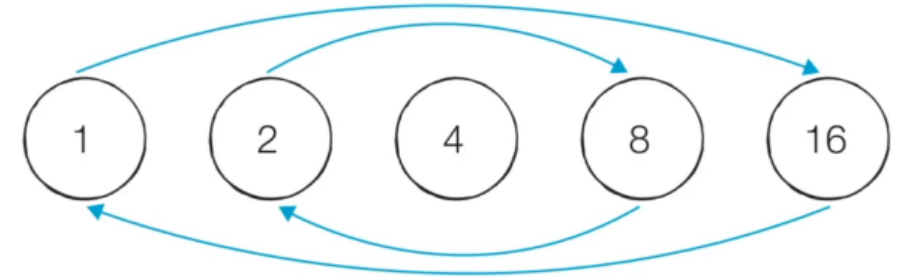
소수는 2보다 큰 자연수 중에서 1과 자기 자신을 제외한 자연수로는 나누어 떨어지지 않은 자연수이다. 예를 들어 7은 1과 7을 제외하고는 나누어 떨어지지 않기 때문에 소수이다. 이러한 소수를 구하기 위한 알고리즘은 크게 2가지가 있다.코드를 작성하기 전에 소수의 특징
11.투 포인터
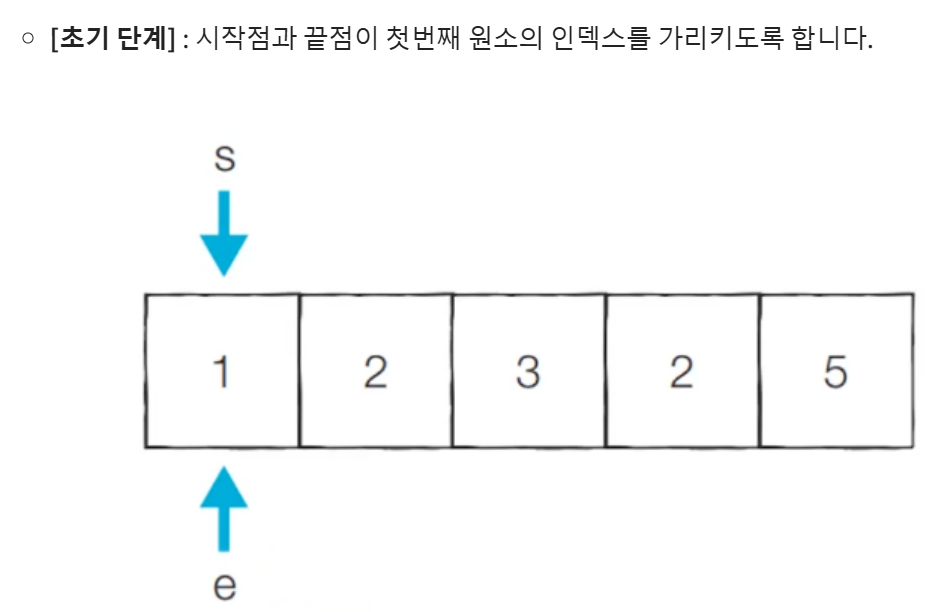
투 포인터 알고리즘은 리스트에 순차적으로 접근해야 할 때 2개의 점 위치를 기록하면서 처리하는 알고리즘을 의미한다. 즉, 시작점과 끝점의 2개의 변수를 이용해 리스트 상의 위치를 기록하여 문제를 해결하는 방식이다. 예시로 특정한 합을 가지는 부분 연속 수열 찾기 문제를