다이나믹 프로그래밍

개요

컴퓨터를 활용해도 해결하기 어려운 문제는 무엇일까? 최적의 해를 구하기에 시간이 매우 많이 필요하거나 메모리 공간이 매우 많이 필요한 문제 등이 컴퓨터로도 해결하기 어려운 문제이다. 따라서 우리는 메모리 공간을 약간 더 사용하여 연산 속도를 비약적으로 증가시키는 다이나믹 프로그래밍을 사용한다.

DP를 사용 X시 문제점

피보나치 수열을 예로 들어보자.

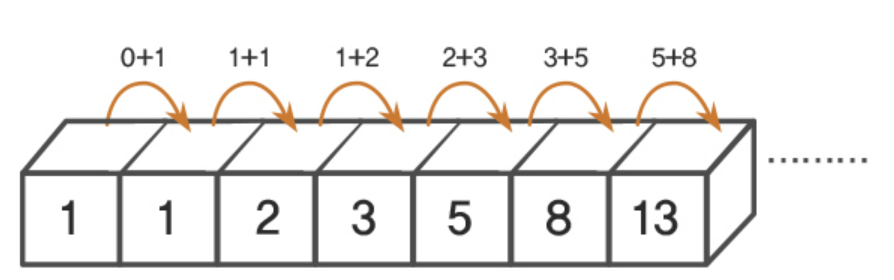
• 피보나치 수열은 이전 두개의 항의 합이 다음항이 되는 수열을 의미한다.
• 점화식은 a_n+2 = a_n+1 + a_n 으로 표현할 수 있다.

#소스코드
def fibo(x):
	if x == 1 or x == 2:
    	return 1
    return fibo(x - 1) + fibo(x - 2)

• 피보나치 수열은 위의 코드처럼 재귀함수로 간단하게 표현할 수 있다.
• 하지만 f(n) 에서 n이 커질수록 수행시간이 기하급수적으로 늘어나는 문제가 있다. f(6)의 호출 과정을 그림으로 그리면 아래와 같다
  
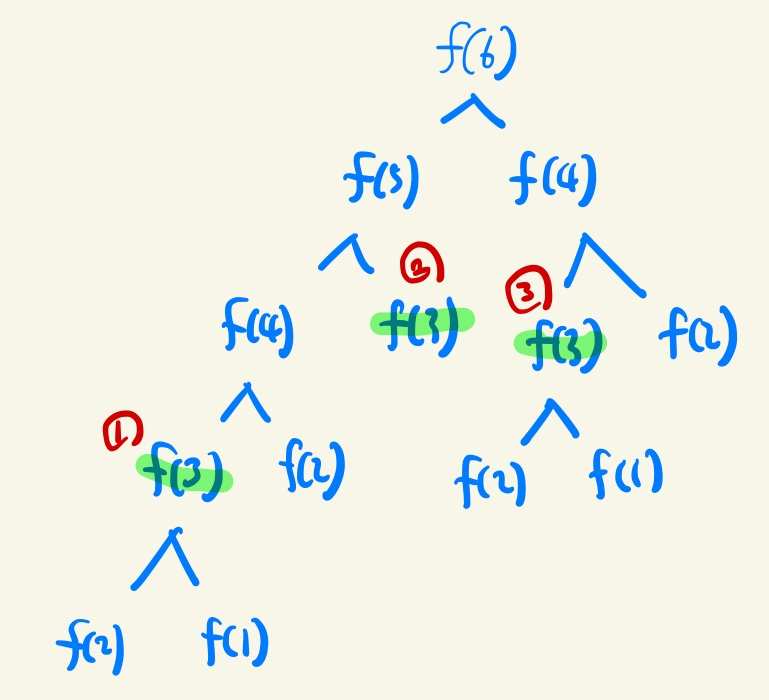
• 위 그림을 참고하면 f(3) 가 3번이나 중복되었음을 알 수 있다. 이는 n이 커지면 커질수록 중복되는 연산이 더 많아져서 시간이 매우 많이 소요될 것이다.

다이나믹 프로그래밍

위의 문제는 다이나믹 프로그래밍을 사용하면 효율적으로 해결할 수 있다. 다이나믹 프로그래밍을 사용할땐느 2가지 조건이 필요하다.

1. 큰 문제를 작은 문제로 나눌 수 있다.
2. 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.

위에서의 연산이 많이 되는 피보나치 수열 문제를 메모이제이션 기법을 사용해서 해결해보자. 메모이제이션은 다이나믹 프로그래밍을 구현하는 방법중 한 종류로 한 번 구한 결과를 메모리에 메모해두고 같은 식을 다시 호출하면 메모한 결과를 그대로 가져오는 기법을 의미한다.

참고) 메모이제이션은 탑다운에서 사용하는 용어이며, 보텀업 방식에서는 DP 테이블 이라고 부른다.

#메모이제이션: 한번 계산된 결과를 리스트에 저장
d = [0] * 100

def fibo(x):
    #종료 조건
    if x == 1 or x == 2:
        return 1
    #연산되지 않은 결과면
    if d[x] != 0:
        return d[x]
    #아직 계산하지 않은 문제라면 점화식에 따라서 결과 반환
    d[x] = fibo(x - 1) + fibo(x - 2)
    return d[x]

• 위 프로그램에서 fibo(99) 를 호출해도 매우 빠른 속도로 정답을 도출한다.
  
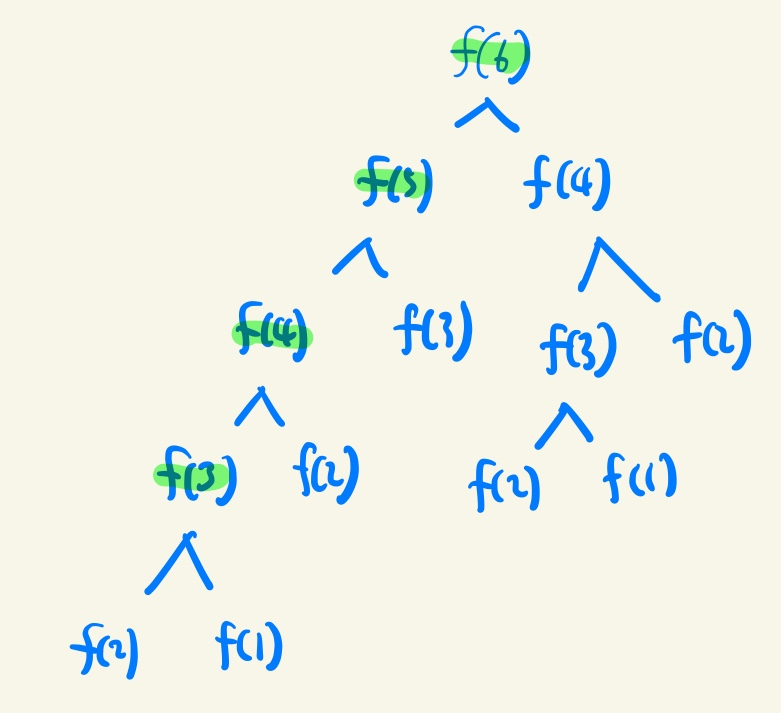
• 메모이제이션을 활용해서 한번 푼 문제의 결과를 저장해 놓았다가 나중에 동일한 문제를 풀어야할 때 이미 저장한 값을 반환한다. 이런 이유로 시간복잡도는 O(N) 임을 알 수 있다.
• 따라서 다이나믹 프로그래밍을 이용하면 중복 연산이 이루어지지 않기 때문에 보다 빠른 속도로 연산이 가능하다.

탑다운 vs 바텀업

탑다운 방식은 처음에 재귀함수를 이용해서 dp를 작성하는 방법을 의미하고, 보텀업 방식은 단순히 반복문을 이용하여 차근차근 답을 도출하는 방식이다. 결론부터 말하면 보텀업 방식을 사용하여 dp를 작성하면 된다. 왜냐하면 탑다운 방식에서는 recursion depth (재귀함수 깊이) 와 관련해서 오류가 발생할 수 있기 때문이다.

보텀업 소스코드

d = [0] * 100

d[1] = 1
d[2] = 2
n = 99
for i in range(3, n + 1):
    d[i] = d[i - 1] + d[i - 2]

탑다운 소스코드

d = [0] * 100

def fibo(x):
    if x == 1 or x == 2:
        return 1
    if d[x] != 0:
        return d[x]
    d[x] = fibo(x - 1) + fibo(x - 2)
    return d[x]