[CS] 인덱스

Index

인덱스는 데이터베이스 테이블에 대하여 검색 속도를 향상시켜주는 자료구조이다.

일상에서의 비슷한 예제로는 단어사전을 생각하면 쉽다. 예를 들어서 특정한 자음 또는 알파벳으로 시작하는 단어를 찾을려고 한다.
해당 단어를 찾기위해서 모든 페이지를 확인할 필요없이 찾고자 하는 부분의 색인에서 찾으면 보다 빠르고 편하게 찾을 수 있다.
데이터베이스에서 index가 이러한 기능을 담당한다.

특정 컬럼에 인덱스를 생성하게 된다면, 해당 컬럼의 데이터들을 정렬하여 별도의 메모리 공간에 데이터의 물리적 주소와 함께 저장이 된다.
이렇게 인덱스가 생성이 되었다면 퀴리문 작성 시 where문으로 조건을 추가하는 등 작업을 하면 옵티마이저에서 판단하여 생성된 인덱스를 탈 수가 있다.
만약 인덱스를 타게 된다면

Optimizer


SQL 쿼리를 가장 효율적으로 실행할 방법을 경정해주는 데이터베이스 엔진의 구성 요소이다.


역활

• 여러개의 실행 계획 중에서 가장 적은 비용이 들어가는 계획을 선택하여 실행을 한다.
  주요 기능
• 각 싱행 계확의 비용을 계산하여 비교한다. 비용은 CPU사용량과 I/O 작업량 등을 기준으로 평가 된다.
• 테이블의 크기, 인덱스의 분포, 데이터 분포 등의 통계 정보를 활용하여 최적의 계획을 선택한다.

종류

인덱스의 종류에 들어가기 전에 간단하게 이진 트리에 대하여 알아보고 넘어가야 B Tree에 대하여 쉽게 이해할 수 있다.

이진 트리

B Tree는 이진 트리에서 잘전되어 모든 리프노드들이 동일한 레벨을 갖도록 자동으로 밸런스를 맞춰 균형을 갖는 트리의 확장판이다.

이진 트리 각각의 상위 노드가 최대 슬하의 두 개의 자식 노드를 갖는 구조이다.

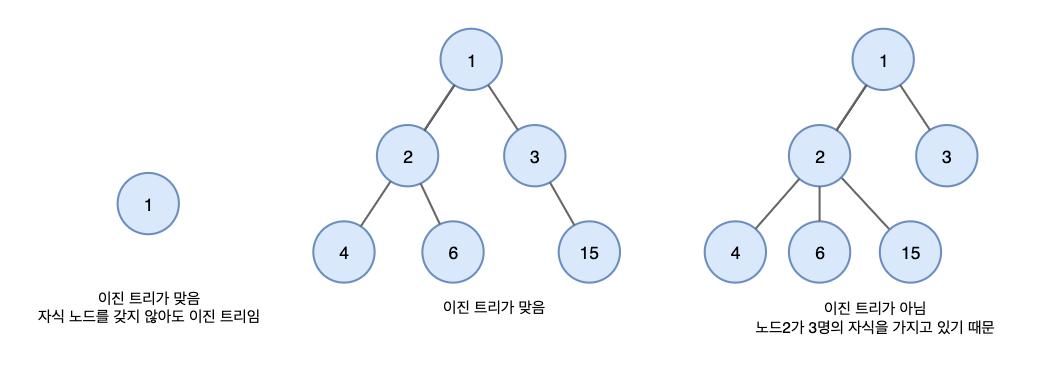
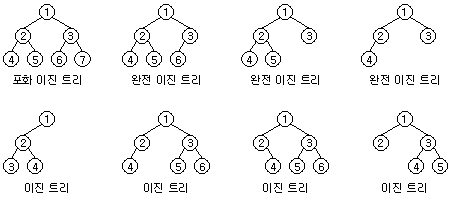
이진트리는 형태에 따라 여러 종류가 있다.

(일단은 이러한 종류가 있다고 알아만 보고 나중에 자세히 알아보겠다.)

B-Tree

가장 일반적으로 사용되는 인덱스의 타입이다.

이는 이진 트리와의 차이점은 하나의 노드에 많은 정보를 갖거나, 두 개 이상의 자식 노드를 취할 수 있다.
하나의 노드에 여러 정보를 담게되며, 여러 자식을 가질 수 있게 되면서 차수라는 개념이 나타났다.

차수


"차수"라는 개념은 B-Tree의 구조와 성능을 결정하는 중요한 요소 중 하나이다. 차수는 아래와 같은 두 가지의 방식에 의하여 정의가 된다.

• 최소 차수 (Minimum Degree, $t$)
  B-Tree의 최소 차수는 $t$로 나타내며, 각각의 노드가 가질수 있는 최소한의 자식 수와 관련이 있다.
  B-Tree의 최소 차수 $t$에 따라 특성을 갖는다.
  • 각 내부 노드는 최소한 $t$개의 자식을 가져야 한다. 그러나 뤁 노드는 이 규칙에서 제외가 되며, 최소한 두 개의 자식이 있으면 된다.
  • 각 내부 노드는 최대 $2t$개의 자식을 가질 수 있다.
  • 각 노드는 최소한 $t - 1$개의 키를 가져야 한다. (루트는 최소 1개)
  • 각 노드는 최대 $2t - 1$개의 키를 가질 수 있다.
    
    
• 최대 차수
  B-Tree의 최대 차수는 각 노드가 가질 수 있는 최대 자식 수로, 보통 $2t$로 정의가 된다. 여기서는 $t$는 최소 차수이다.
  
  
  이러한 규칙은 균형을 유지하는데 중요하다. 예를 들어서 $t$=3인 B-Tree에서 각 노드가 최소 2개의 키와 최대 5개의 키를 가질 수 있으며, 각 내부 노드는 최소 3개의 자식과 최대 6개의 자식을 가질 수 있다.
  
  
  B-Tree에서 차수는 트리의 높이를 낮추고, 디스크 접근을 줄이며, 삽입, 삭제, 검색 등의 연산을 효율적으로 수행하는데 중요한 역활을 한다. 따라서, 차수는 B-Tree의 성능과 저장 구조과 저장 구조를 결정하는데 핵심적인 매개변수이다.

B-Tree를 예제를 들어서 설명을 하면
블럭 = 서랍, 데이터 = 편지 라고 가정을 하겠다.
편지 하나를 큰 서랍에 넣는다고 생각을 할 때, 서랍의 크기는 2KB인데 편지 하나만 서랍에 넣어두면 해당 서랍은 3byte의 크기인 편지하나와 빈 공간의 서랍이 된다.
이때 서랍을 여닫을 때 드는 비용은 해당 서랍이 비어 있든, 가득 차 있든 들어가는 비용은 동일하다. 즉, 공간이 낭비되는 것이다.

B-Tree는 하나의 노드(서랍)에 여러 개의 데이터를 저장하여 블럭을 최대한 활용을 한다.
이제 서랍에 여러 개의 편지를 넣어 관리를 한다. 편지 여러 장을 한 서랍에 넣으면 서랍을 여닫는 횟수를 줄일 수 있고, 서랍 하나당 더욱 많은 데이터를 저장할 수 있다. 이를 통하여 서랍을 효율적으로 관리할 수 있다.

B-Tree는 데이터를 정렬하고 조직화 하여 저장을 한다. 따라서 필요한 데이터를 빠르게 찾을 수 있고, 블럭(서랍)을 확인하는 횟수가 줄어든다.
추가적으로 여러 데이터를 넣으면, 필요한 데이터를 한 번에 더 많이 처리할 수 있다.

이러한 B-Tree는 항상 균형을 유지하므로, 트리의 높이가 낮아진다. 이는 데이터 검색, 삽입, 삭제 시 연산 시간을 일정하게 유지하는 데 도움이 된다. 그리고 블럭 단위로 데이터를 저장하므로, 하나의 노드에 여러 키와 포인터를 저장한다. 그렇기 때문에 디스크 I/O를 줄이는 부분에서 도움이 된다.

B-Tree는 모든 연산(검색, 삽입, 삭제)이 $O(lob$ $n)$의 시간 복잡도를 가지므로, 데이터 양이 많이져도 성능은 크게 저하되지 않는다.

B-Tree 예

1. 초기 상태
   리프 노드 [2, 4, 6]

2. 데이터 삽입 후 분할

   • 키 8을 삽입
   • 리프 노드가 가득 차므로 분할이 필요하다.

       [4]
     /    \
 [2, 4]  [6, 8]

3. 데이터 삽입 후 분할
   • 키 10을 삽입 후 리프 노드 분할

분할 전
       [4]
     /    \
 [2, 4]  [6, 8, 10]

분할 후
         [4, 10]
       /    |    \
 [2, 4]  [6, 8]  [10, 12]

특징

• 데이터 노드의 자료는 정렬되어 있다.
• 자료는 중복되지 않는다.
• 모든 리프 노드는 같은 레벨상에 있다.
• 루트 노드는 자신이 리프 노드가 되지 않는 이상 적어도 2개 이상의 자식 노드를 갖느다.
• 루트 노드와 리프 노드를 제외한 노드들은 최대 M개 부터 최소 M/2개 까지의 자식을 가질 수 있다.
• 노드의 키는 최대 M-1개부터 최소(M/2)-1개의 키가 포함될 수 있다.
• 자식 수의 하한값을 $t$라고 하면, M=2$t$-1을 만족한다.

---

B*Tree

B*Tree 인덱스는 B-Tree의 한 변형으로 B-Tree는 노드가 가득 차면 즉시 분할하므로, 분할이 자주 발생할 수 있다는 부분과 노드가 반쯤 비어있는 경우가 많아서 디스크 공간을 비효율적으로 사용하게 된다는 문제점이 있어 이를 해결하기 위해서 개발되었다.

B*Tree의 각 노드는 B-Tree의 노드보다 더 많은 자식 노드를 가질 수 있다. 그리고 노드가 분할될 때, 분할된 데이터를 인접 노드로 분산시켜 트리의 균형을 유지한다. 마지막으로 노드 분할 시 인접 노드와 데이터를 재배치하여 공간 활용을 최적화 한다.

B-Tree와의 차이점으로 최소 M/2개의 키값을 가져야 했던 기존 노드의 자식 노드 수 최소 제약 조건이 2M/3로 증가하고, 노드가 가득 타면 분할 대신에 인접 노드와 데이터를 재배치를 한다.
(만약 추가적인 재배치가 불가능 할 경우는 분할을 한다.)

B*Tree 예

1. 초기 상태

   • 리프 노드 : [2, 4, 6]
   • 인접 노드 : [10, 12]

2. 데이터 삽입

   • 키 8을 삽입

        [6]
      /    \
 [2, 4]  [8, 10, 12]

3. 인접 노드로 분할

         [6, 10]
       /    |    \
 [2, 4]  [8]  [10, 12]

특징

• 데이터 노드의 자료는 정렬되어 있다.
• 자료는 중복되지 않는다.
• 모든 리프 노드는 같은 레벨상에 있다.
• 루트 노드는 자신이 리프 노드가 되지 않는 이상 적어도 2개 이상의 자식 노드를 갖느다.
• 루트 노드가 아닌 노드들은 적어도 2[(M-2)/3]+1개의 자식 노드를 갖고 있다.

---

B+Tree

B-Tree에서 내부 노드와 리프 노드 모두에 키와 데이터를 저장한다. 이는 데이터가 많을수록 검색 성능이 떨어지는 문제점이 있고, 범위 검색에 있어서 모든 리프 노드를 순차적으로 탐색해야 하기 때문에 비효율적이다. 이러한 문제점을 극복한 B+Tree가 나타났다.

B+Tree의 내부 노드와 리프 노드의 분리를 했다.
내부 노드는 키만 저장하고ㅡ 리프 노드는 키와 데이터 모드를 저장을 한다. 그리고 모든 실제 데이터는 리프 노드에만 저장이 되며, 내부 노드는 데이터 검색을 위한 경로를 제공한다.

리프 노드들은 연결 리스트 형태로 연결되어 있다. 이는 범위 검색과 순차 접근을 더 효율적으로 만든다.

B-Tree와 마찬가지로 항상 균형을 유지한다. 그래서 삽입과 삭제 시 자동으로 균형을 맞춘다.

B+Tree 예

• 내부 노드 : 키만 저장하며, 자식 노드를 가리키는 포인터를 포함한다.
• 리프 노드 : 키와 데이터를 모두 저장하며, 다음 리프 노드를 가리키는 포인터를 포함한다.

1. 초기 B+Tree
   • 리프 노드 : [2, 4, 6, 8]
   • 내부 노두 : [4] (두 자식 노드를 가리킴)

     [4]
   /    \
[2, 4]  [6, 8]

2. 데이터 삽입
   • 새로운 키 10을 삽입한다. 리프 노드 [6, 8]에 공간이 있으므로 키 10을 삽입한다.
   • 리프 노드 : [2, 4], [6, 8, 10]

       [4]
     /    \
 [2, 4]  [6, 8, 10]

3. 리프 노드 분할
   • 새로운 키 12를 삽입하면 리프 노드 [6, 8, 10]이 가득 차므로 분할이 필요하다.
   • 리프 노드 분할 후 : [6, 8], [10, 12]
   • 내부 노드 갱신 : [4, 10]

         [4, 10]
       /    |    \
 [2, 4]  [6, 8]  [10, 12]

4. 범위 검색
   • B+Tree 에서 6에서 12 사이의 데이터를 검색하면, 리프 노드 [6,8] 부터 [10, 12] 까지 순차적으로 접근하여 데이터를 효율적으로 검색할 수 있다.

특징

• 데이터 노드의 자료는 정렬되어 있다.
• 데이터 노드에서는 데이터 중복되지 않는다.
• 모든 리프 노드는 같은 레벨상에 있다.
• 리프 노드가 아닌 노드의 키값의 수는 그 노드의 서브트리수보다 하나가 적다.
• 모든 리프 노드는 연결 리스트로 연결되어 있다.

---

해시 인덱스 (Hash Index)

K-V 쌍을 기반으로 데이터의 위치를 빠르게 찾을 수 있다.
정확한 값 검색에 뛰어나지만 반대로 범위 검색에는 적합하지 않다.
MySQL에서는 MEMORY 엔진에서 주로 사용된다.

비트맵 인덱스 (Bitmap Index)

이는 데이터 값의 카디널리티가 낮은 경우에 유용하다.
각각의 행의 상태를 비트맵으로 저장하여 대량의 데이터에 빠른 집계와 논리연산이 가능하다.

클러스터 인덱스(Clustered Index)

테이블의 데이터 자체를 정렬된 구조로 저장을 한다.
한 테이블에 하나만 생성할 수 있으며, 주로 기본키에 대해 설정이 된다.
데이터가 물리적으로 정렬되기 때문에 매우 빠른 데이터 접근이 가능하게 한다.

비클러스터드 인덱스 (Non-Clustered Index)

데이터와 인덱스를 별도로 저정한다.
여러 개를 생성할 수 있으며, 테이블 내 특정 컬럼에 대한 검색 성능을 향상시킨다.

장점

인덱스 사용으로 데이터 검색에 있어서 빠르게 결과를 얻을 수 있다. 기존에는 전체 데이터를 확인을 했지만 이제는 전체 데이터를 확인하지 않고 찾을 수 있으며
특히 WHERE JOIN ORDER BY GROUP BY 사용에 유용해졌다.