[알고리즘] 에라토스테네스의 체

소수를 구하는 알고리즘으로 유명한 $에라토스테네스의 체$ 관련해서 정리를 해보겠다.

$에라토스테네스의 체$를 알아보기 전에 기본적인 소수 판정법에 대하여 간단하게 알아보는 것이 좋다고 생각하기 때문에 소수 판정법을 먼저 보겠다.

소수 판정법

자연수 $N$이 소수인지 판정하는 방법에 대해서 보겠다.

• 단순한 소수 판정 기법

  정수 $N$이 주어질 때 $2$~$N-1$까지의 자연수로 나누어 떨어지지 않는 수인지 확인을 하며 $N$이 소수라는 것에 대하여 판정이 가능하다.

	static boolean isPrime(long N) {
		// 2 이상의 정수 N을 매개변수로 받고, N이 소수라면 True를,
		// 아니라면 False를 리턴하는 함수
		for (long i = 2; i <= N - 1; i++) {
			if (N % i == 0) {
				return false; // N이 i으로 나누어지는 경우, 이 시점에서 소수가 아니라는 것을 알 수 있음
			}
		}
		return true;
	}

하지만 복잡도가 $O(N)$이므로 굉장히 오래 걸린다.

• 빠른 소수 판정 방법

  앞에서 확인한 방법에서 $2$~$N-1$ 까지 모두 확인할 필요가 없다.

  $|\sqrt{2}|$까지만 나누어보면 소수인지 판정할 수 있다.

  반대로 모든 합성수는 2 이상 $\sqrt{2}$ 이하로 반드시 나누어 진다.

  예를 들어$N=53$ 일 때 한번 확인을 해보면
  $7<\sqrt{53}<8$ 이기 때문에 $1$~$7$까지의 수로 나누어보면 해당 $N$은 소수로 정의가 된다.

  또다른 예로 $N=77$ 일 때 보면
  $8<\sqrt{77}<9$ 이기 때문에 $1$~$8$까지의 수로 나누어보면 해당 $7$일 때 나누어지기 때문에 $N$은 소수가 아닌 합성수라고 판정이 된다.
  

	static boolean isPrime(long N) {
		// 2 이상의 정수 N을 매개변수로 받고, N이 소수라면 True를,
		// 아니라면 False를 리턴하는 함수
		for (long i = 2; i * i <= N; i++) {
			if (N % i == 0) {
				return false;
			}
		}
		return true;
	}

• 응용 예

  $N$의 모든 약수 출력하기

  이와 같은 문제가 있을 때 앞에서 빠른 소수 판정 방법을 이용하면 상당히 쉽게 해결이 된다.
  1. $i=1,2,3,..,\sqrt{N}$일 때, $N$이 $i$로 나누어지는지 확인
  2. 나누어지는 경우 $i$와 $N/i$는 약수이기 때문에 $i$와 $N/i$을 출력하면 된다.

     for (long i = 1; i * i <= N; i++) {
     	if (N % i == 0) {
     		System.out.println(i); // i를 약수로 추가
     		if (i != N / i) {
     			System.out.println(N / i); // i ≠ N/i라면, N/i도 약수에 추가
     		}
     	}
     }

이렇게 간단하게 간편한 소수 판정 방법에 대하여 알아 보았다.

---

에라토스테네스의 체

고대 그리스의 수학자 에라토스테네스가 만들어 낸 소수 판정 기법이다.
이 방법은 마치 체로 수를 걸러낸다 하여 '에라토스테네스의 체' 라고 부른다.
이는 지표함수 $f(x) = x/1_P(x)$의 수열을 표로 시각화한 것이라 볼 수 있다.

• 동작 방법

  1. 정수 $2$부터 $N$까지 모든 수를 나열
  2. 별다른 동작이 없는 가장 작은수 2를 기준으로 배수가 되는 수는 지운다.
  3. 별다른 동작이 없는 가장 작은수 3를 기준으로 배수가 되는 수는 지운다.
  4. 위 $+1$을 하여 계속 진행을 한다.

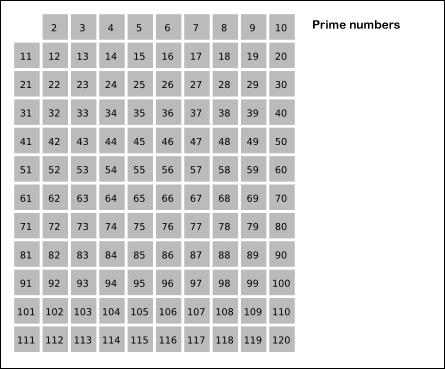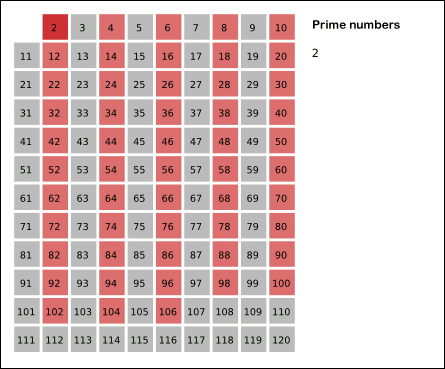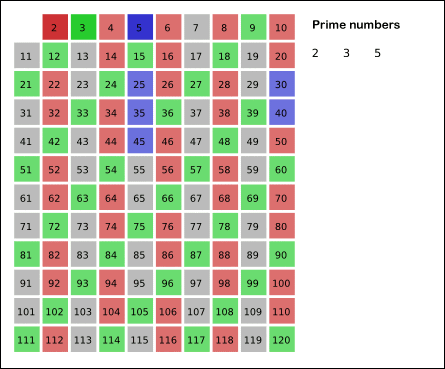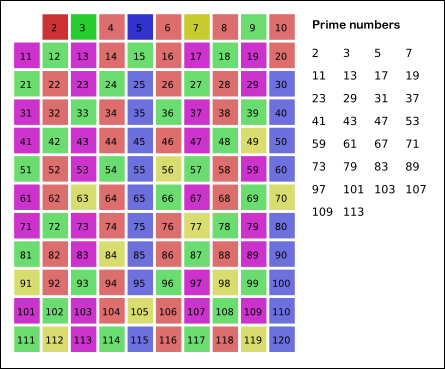
위 이미지에서 보듯이 각 배수를 제거하고 남은 수들 모두가 소수이다.

$에라토스테네스의 체$를 Java 코드로 구현을 하면 아래와 같이 구현할 수 있다.

		boolean[] prime = new boolean[N + 1];
		for (int i = 2; i <= N; i++) {
			prime[i] = true;
		}
		
		// 에라토스테네스의 체
		for (int i = 2; i * i <= N; i++) {
			if (prime[i] == true) {
				for (int x = 2 * i; x <= N; x += i) {
					prime[x] = false;
				}
			}
		}