
탐욕법(그리디) 알고리즘이란?
Greedy의 뜻은 '탐욕스러운, 욕심이 많은'의 의미를 갖고 있다.
해당 알고리즘은 선택의 순간에 최적의 상황만을 찾아 최종적인 답에 도달하는 알고리즘이다.
하지만 가장 좋은 결과는 최종적인 결과 도출에 대한 최저의 해를 보장해주는 것이 아니다.
예를 들어 어떤 문제에서 그리디 알고리즘을 이용하여 최적의 해를 찾을려고 할 때, 각 단계에서 가장 좋은 선택을 한다고 생각을 하자
하지만 이 선택이 전체적으로 최적한 것이라고 보장은 할 수 없다.
동작 원리
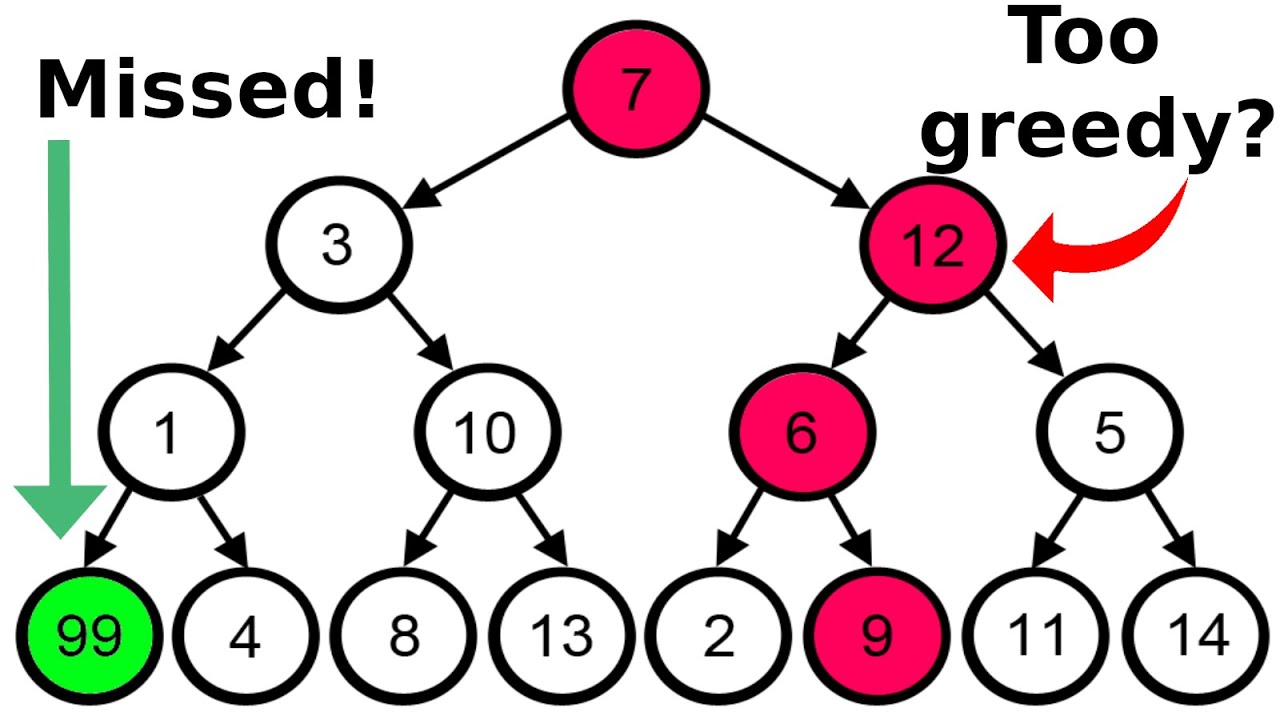
탐욕법의 문제 해결 방법으로는
1. 문제의 최적의 해를 선택하는 기준을 정한다.
2. 문제의 구조에 맞는 선택 절차를 정의
선택 절차(Selection Procedure) : 현 상태에서 최적의 해답을 선택
3. 조건에 만족하지 않는 해는 과감하게 제외
적절성 검사(Feasibility Check) : 선택된 해답이 문제의 조건을 만족하는지 검사
4. 선택이 완료되면 해답이 조건을 만족하는지 검사.
해답 검사(Solution Check) : 본래의 문제가 해결되었는지 검사하고, 만약 해결이 되지 않았다면 선택 절차로 돌아가 위 과정을 반복한다.
조건
탐욕 알고리즘을 적용하기 위해서는 2가지 조건에 만족을 해야한다. 해당 알고리즘이 잘 동작하기 위해서는 대부분 탐욕스러운 선택 조건(Greedy Choice Property)과 최적 부분 구조 조건(Optimal Substructure)라는 조건에 만족을 해야 한다.
탐욕스러운 조건은 앞의 선택이 이후의 선택에 영향을 주지 않는다는 것이고, 최적의 부분 구조 조건은 문제에 대한 최적의 해가 부분 문제에 대해 역시 최적의 해라는 것이다.
탐욕스러운 선택 조건 : 각 단계에서의 선택이 전테적인 최적의 해를 구하기 위한 최적해의 부분 집합에 속한다는 것을 의미한다.
즉, 간단히 설명을 하면 각 Step에서의 선택이 지역적으로는 최적이지만, 선택들이 모여 전체적으로도 최적의 해를 구성한다는 특성
최적 부분 구조 조건 : 큰 문제의 최적해가 작은 부분 문제의 최적해를 포함 한다는 특성을 의미한다.
즉, 큰 문제를 작은 부분 문제로 나눌 수 있으며, 작은 부분 문제의 최적해를 결합하여 전체적인 문제의 최적의 해를 얻을 수 있다는 것을 나타낸다.
이러한 조건을 갖는 탐욕 알고리즘은 주로 적용되는 분야는 최소 신장 트리 문제, 최단 경로 문제, 탐욕적 스케줄링 문제, 배낭 문제의 일부 변형으로 알고리즘이 적용되어 효율적이고 유용한 해결 방안이 된다.
장점과 단점
- 장점
- 간단하고 직관적인 구현이 가능하며, 일반적으로 계산의 효율성이 높다.
- 일부 문제에 대하여 최적의 해를 빠르게 찾을 수 있다.
- 탐욕 알고리즘이 문제에 적합한 경우, 빠른 해결책을 제공해준다.
- 단점
- 항상 최적의 해를 보장하지 않는다. 때로는 근사해에 머무를 수 있다.
- 탐욕적 선택이 지역적으로는 최적이지만 전체적으로는 최적이 아닐 경우가 있다.
- 일부 문제에는 탐욕 알고리즘이 적용되지 않거나 잘못된 결과를 갖고온다.
이렇게 간단한 장점과 단점을 정리했다.
예제
거스름돈을 줄 때 가장 적은 동전의 개수로 거슬러 줘야 한다. 사용이 가능한 동전의 종류로 500,100,50,10의 단위가 있다고 할 대
적용 방법으로는
- 주어진 금액에서 가장 큰 단위의 동전부터 선택을 한다.
- 선택된 동전을 사용하여 주어진 거스름 금액을 최대한 많이 거슬러 준다.
- 남은 거스름 금액을 앞선 과정을 반복한다.
간단하게 코드로 구현을 하면 아래와 같이 구현을 했다.
public static void main(String[] args) {
int[] coins = {500, 100, 50, 10}; // 동전의 종류
int amount = 1260; // 거슬러 줄 금액
int[] result = makeChange(coins, amount);
System.out.println("거스름돈 개수:");
for (int i = 0; i < coins.length; i++) {
System.out.println(coins[i] + "원: " + result[i] + "개");
}
}
public static int[] makeChange(int[] coins, int amount) {
int[] change = new int[coins.length]; // 동전의 개수를 저장할 배열
Arrays.sort(coins); // 동전의 종류를 오름차순으로 정렬
// 가장 큰 단위의 동전부터 시작하여 거스름돈 계산
for (int i = coins.length - 1; i >= 0; i--) {
change[i] = amount / coins[i]; // 해당 동전으로 거슬러 줄 개수 계산
amount %= coins[i]; // 남은 금액 업데이트
}
return change;
}