
이전 포스트에서는 Union-Find 기법을 통한 서로소 집합 알고리즘을 알아봤다.
서로소 집합 알고리즘을 응용하면 그래프의 싸이클 판별과 크루스칼 알고리즘 등을 구현할 수 있다.
이번에는 그래프의 싸이클 판별에 대해 알아보고자 한다.
1. 그래프의 Cycle 판별
그래프에서 Cycle이 존재한다는 것은 순환 그래프라는 것을 의미한다.
즉, 특정 노드에서 출발하여 간선을 한 번씩 지나 다시 출발 노드로 돌아올 수 있다면 싸이클이 존재하는 것이다.
아래의 첫 번째 그림은 싸이클이 존재하지 않는 경우, 두 번째 그림은 싸이클이 존재하는 경우이다.
-
싸이클이 존재하지 않는 그래프
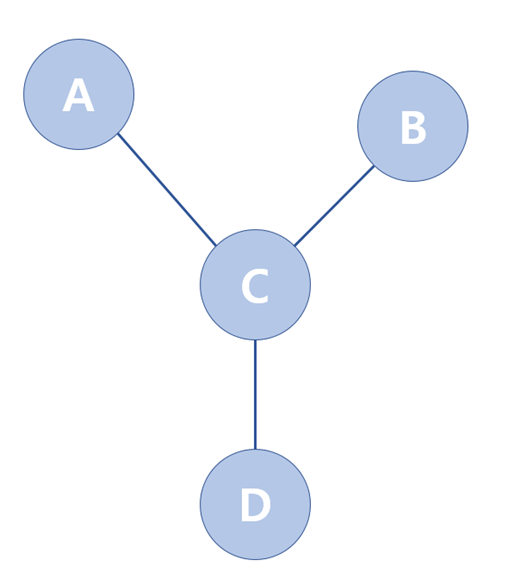
-
싸이클이 존재하는 그래프 (순환 그래프)
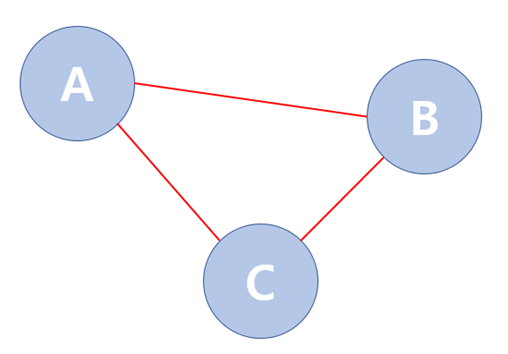
싸이클 판별은 Union-Find를 통해 다음과 같은 과정으로 찾을 수 있다.
1. 각 노드의 부모 테이블을 자기 자신으로 초기화
2. 두 노드 씩 연결 정보를 받아 루트 노드를 탐색 (Find 연산)
- 두 노드의 루트 노드가 다르다면 Union 연산
- 두 노드의 루트 노드가 같다면 Cycle 존재
위 과정의 원리를 살펴보면 모든 노드에 대한 부모 테이블이 처음에 자기 자신으로 초기화 되어 있으며 두 노드씩 Find 연산을 통해 루트 노드를 탐색했을 때 같은 루트 노드를 갖는다는 것은 이미 연결된 노드가 다른 간선으로 또 한 번 연결되었다는 것을 의미한다. 즉 반드시 싸이클이 존재한다는 것을 의미할 것이다.
아래 예시 그래프를 통해 위 과정을 차례대로 수행해 보자.
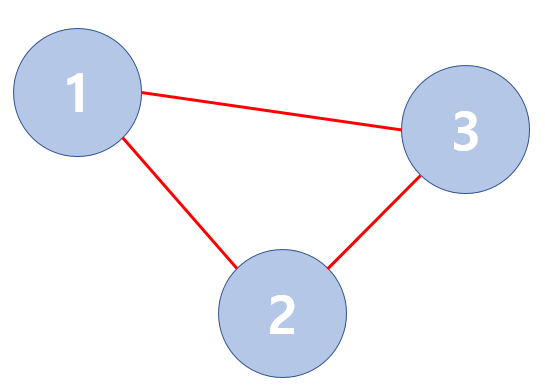
먼저 부모 테이블을 초기화 한다.
| 노드 | 1 | 2 | 3 |
|---|---|---|---|
| 부모노드 | 1 | 2 | 3 |
그다음 각 노드의 연결 정보가 주어졌을 때 Find 연산을 통해 루트 노드를 찾는다.
노드 1과 2를 계산해보자.
노드 1의 루트 노드는 1, 노드 2의 루트 노드는 2이므로 다른 루트 노드를 가지고 있다.
이 경우 Union 연산을 통해 두 노드를 같은 집합에 속하게 한다. 이때, 크기가 작은 노드 1이 노드 2의 부모가 되고 아래와 같이 부모 테이블이 초기화 된다.
| 노드 | 1 | 2 | 3 |
|---|---|---|---|
| 부모노드 | 1 | 1 | 2 |
다음 노드 2와 3의 경우도 동일한 과정을 거쳐 아래와 같이 부모 테이블을 초기화 한다.
| 노드 | 1 | 2 | 3 |
|---|---|---|---|
| 부모노드 | 1 | 1 | 1 |
마지막으로 노드 2와 3의 연결 정보를 통해 위 과정을 수행하면
노드 2와 3의 루트 노드는 1로 동일하므로 이미 연결된 두 노드를 한 번 더 연결한 것으로 해석된다.
즉, 그래프 그림과 같이 싸이클이 존재한다.
소스 코드는 다음과 같다.
def find_parent(parent, x):
if parent[x] != x:
parent[x] = find_parent(x, parent[x]) #경로 압축 기법
return parent[x]
def union(a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a > b:
parent[a] = b
else:
parent[b] = a
v, e = map(int, input().split()) # v: 노드의 수, e: 간선의 수
parent = [0] * v
for i in range(v): #부모 테이블 초기화
parent[i] = i
for _ in range(e):
a, b = map(int, input().split())
if find_parent(a) == find_parent(b): #두 노드의 루트 노드가 같은 경우 싸이클 존재
print("Cycle이 존재합니다.")
return
else: #두 노드의 루트 노드가 같지 않다면 Union 연산
union(a, b)
print("Cycle이 존재하지 않습니다.")Find 연산의 경우 부모 테이블을 재귀적으로 거슬러 올라갈 필요 없이 시간 복잡도를 최적화 하기 위해
경로 압축법을 사용했다.
이렇게 싸이클 판별 알고리즘을 알아봤다.
Union-Find 알고리즘을 살짝 응용했을 뿐 추가적으로 더 어려운 로직이 들어가있진 않아 어렵지 않게 이해할 수 있다.
다음에 작성핧 크루스칼 알고리즘은 이러한 싸이클 판별을 응용하여 구현할 수 있다.
크루스칼 알고리즘은 많은 문제에 등장하는 만큼 다음 포스트에서 따로 다루려고 한다.
