
이전 포스트에서 다뤘던 Union-Find 기법을 통한 서로소 집합 알고리즘과 이를 통한 싸이클 판별을 이용해서 크루스칼 알고리즘을 구현해보고자 한다.
Kruskal Algorithm은 싸이클 없이 최소 비용의 간선을 택하여 모든 노드를 연결하는 그래프이론이다.
모든 노드를 연결할 때, 최소 비용이 드는 간선을 택한 경우를 최소신장트리라고 한다.
크루스칼 알고리즘은 노드와 간선 정보가 주어졌을 때 해당 그래프를 최소신장트리로 만들기 위한 알고리즘이다.
먼저, 신장트리와 최소신장트리 구조를 알아보자.
1. 신장 트리 (Spanning Tree)
최소신장트리를 알기 이전에, 신장트리를 먼저 알아야한다.
신장트리는 싸이클 없이 모든 노드가 연결되어 있는 특수한 트리 구조이다.
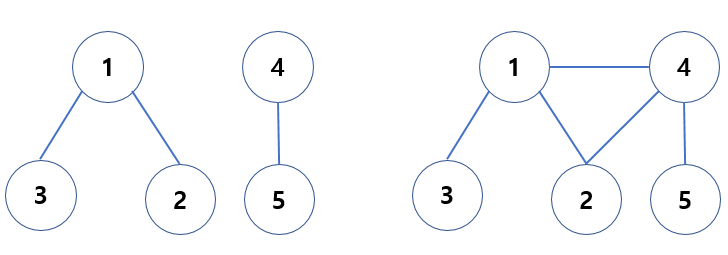
아래 두 그래프 모두 신장트리가 될 수 없다.
왼쪽 그림의 경우, 간선이 모든 노드를 연결하지 않고 두 개의 부분집합으로 나누어진다.
오른쪽 그림의 경우 모든 노드가 연결되어 있지만 노드 1과 노드 4를 연결하는 간선을 통해 싸이클이 형성되었다. 싸이클이 존재한다는 것에서 해당 그래프는 트리가 아니게 된다.
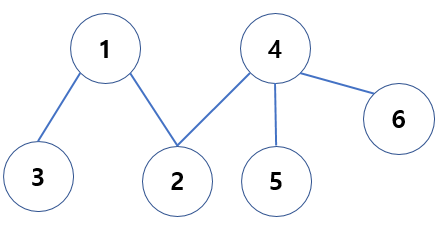
아래 그림의 경우는 간선을 통해 모든 노드가 연결되어 있으며 싸이클이 존재하지 않으므로 신장트리라고 할 수 있다.
2. 최소 신장 트리 (MST, Minimum Spanning Tree)
MST라고도 불리는 최소 신장 트리는 비용이 정의된 간선 정보가 주어졌을 때 해당 그래프로 만들 수 있는 신장 트리 중에서 비용이 가장 적게 드는 신장 트리를 의미한다.
최소 신장 트리의 특징은 다음과 같다.
- V개의 노드가 있을 때 V-1 개의 간선으로 이루어진다.
- 싸이클이 존재하지 않는다.
- 간선 가중치의 합이 최소이다.
예를 들어 아래의 그래프가 주어졌다고 가정해보자.
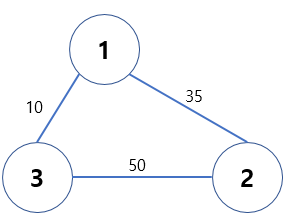
위 그래프의 3개의 노드를 모두 연결하는 간선의 개수는 2개가 되어야 하므로 만들 수 있는 신장 트리는 아래와 같이 세 가지이다.
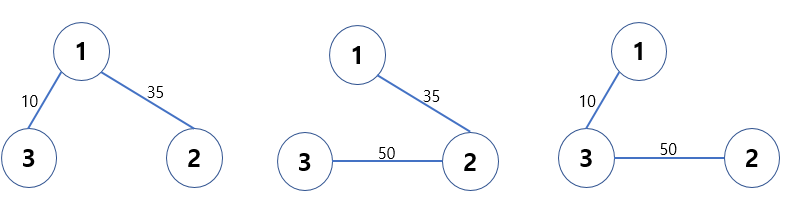
세 개의 신장 트리 중에서 가중치의 합은 각각 다음과 같다.
1) 10 + 35 = 45
2) 35 + 50 = 85
3) 10 + 50 = 60
계산 결과와 같이 해당 그래프의 최소 신장 트리는 첫 번째 그림이 되고 이 때의 비용은 총 45이다.
3. 크루스칼 알고리즘 (Kruscal Algorithm)
최소 신장 트리를 알았으면, 크루스칼 알고리즘을 알아보자.
크루스칼은 그리디 알고리즘의 일종이다. 즉, 눈 앞에 가장 이득이 되는 케이스를 탐욕적으로 택한다는 것.
여기서 이득이 되는 것은 아무래도 간선의 비용이 가장 적은 것이라고 할 수 있겠다.
노드와 간선의 정보가 주어졌을 때 크루스칼 알고리즘의 프로세스는 아래와 같다.
- 간선 정보를 비용에 대하여 정렬한다.
- 정렬된 간선에 대해 비용이 적은 순으로 싸이클을 발생시키는지 확인한다.
- 싸이클을 발생시키는 간선은 버리고 싸이클을 발생시키지 않는 간선만 택한다.
위와 같은 과정으로 모든 간선을 탐색하면 싸이클이 발생하지 않는 가장 낮은 비용의 간선들만 선택되며 그 결과는 최소 신장 트리가 된다.
이전에 다뤘던 Union-Find와 싸이클, 최소 신장 트리에 대한 개념만 알고 있다면 크루스칼 알고리즘을 구현하는 것은 굉장히 쉽다.
아래는 노드 수 V, 간선 수 E와 각 간선의 연결 정보가 주어졌을 때,
크루스칼 알고리즘을 통해 최종적으로 도출된 최소 신장 트리의 간선 비용 합을 구하는 코드이다.
def find_parent(parents, x):
if parents[x] != x: #경로 압축법을 통한 find 구현
parents[x] = find_parent(parents, x)
return parents[x]
def union(a, b):
a = find_parent(parents, a)
b = find_parent(parents, b)
if a < b:
parents[b] =a
else:
parents[a] = b
v, e = map(int, input().split())
edges = []
result = 0 # 최종적으로 결정되는 최소 신장 트리의 간선 비용 합
parents = [0] * len(v)
for i in range(len(v)): # 부모 테이블 초기화
parents[i] = i
for _ in range(e):
a, b, cost = map(int, input().split())
edges.append((cost, a, b))
edges.sort() #비용이 적은 간선부터 싸이클을 판별하기 위해 간선 정보 sorting
for cost, a, b in edges: #두 간선의 루트가 다르면 (싸이클이 발생하지 않으면)
if find_parent(parents, a) != find_parent(parents, b)
union(a, b) # 두 노드 연결
result += cost
print(result)
이렇게 Union-Find로 시작해서, Cycle 판별, 최소 신장 트리와 크루스칼 알고리즘을 알아봤다.
다음 포스팅에선 그래프 이론의 마지막으로 Topology Sorting (위상 정렬)을 다뤄볼 예정이다. 🚀
