Normalization

일반적으로 정규화는 통계에서 평균과 표준편차를 통일되게 맞추어 통계적 접근을 용이하고 쉽게하기 위함에 있다. 하지만 이러한 용도 이외에 심층학습에서 정규화는 신경망의 보다 용이한 학습을 도와준다고 알려져 있다.

Batch Normalization

---

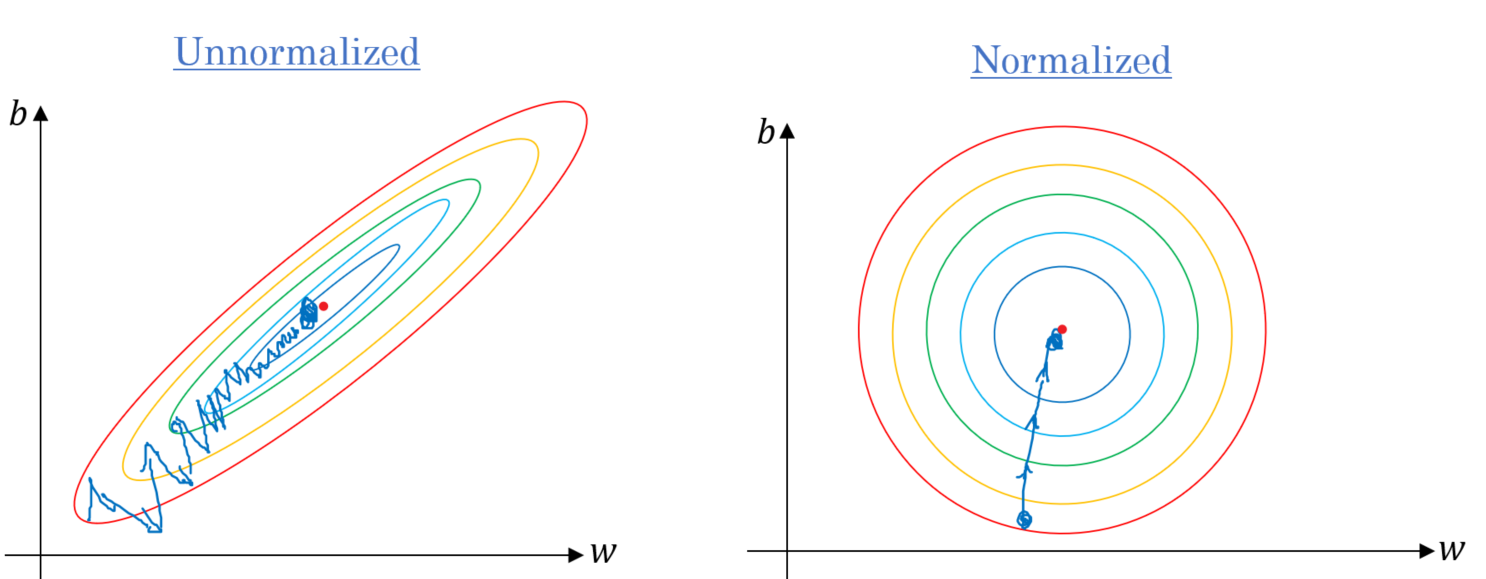
위의 사진을 보게되면 정규화를 진행한 형태의 모습이 보다 안정되고 일관된 학습을 진행하기 용이하다는 것을 직관적으로 알 수 있을 것이다. 심층학습에서의 정규화는 화성함수 이후에 진행되는 방식($A$)과 황성함수 이전에 진행되는 방식($Z$)로 나눌 수 있다. 우리는 활성함수 이전에 정규화를 하는 과정에 대해서 알아볼 것이다.

위의 식은 특정 은닉층에서의 회귀 값에 대한 정규화 과정을 나타낸 것으로 일반적인 평균과 표준편차(분산)을 구하는 과정과 동일하다.

평균을 0으로 표준편차를 1로 바꾸는 것은 표준 정규화를 시키는 것으로 각 훈련에서 모든 데이터 예제들이 가장 잘 훈련되는 정규화 정도는 각각 다르기 때문에 실제로는 $\tilde{z}$를 이용하여 $\beta$와 $\gamma$를 통해서 정규화를 하게 된다.

Why does it works?

---

그렇다면 정규화는 왜 학습을 더욱 빠르게 할 수 있는가? 공변량 이동(Covariate shift)를 통해 그 이유를 살펴보자.

Covariate shift

Covarate shift appears only in $X \rarr Y$ problems, and is definded as the case where $P_a(y|x)=P_b(y|x)$ and $P_a(x)\ne P_b(x)$.

공변량 이동은 $X$와 $Y$와 관련된 사상(mapping)에 대해서는 차이가 없지만 실제 분포가 동일하지 않아서 모델을 적용함에 있어 차이가 생기는 현상을 말한다.

• 흑백 고양이를 이용한 분류 모델을 색깔 사진 고양이 분류에 적용하는 경우.
• 젊은 얼굴로 학습시킨 내용을 노인들을 대상으로 적용하는 경우.

위와 같은 경우에서 학습에서 얻은 성능만큼을 끌어낼 수 없는 상황에 놓인다. 이와 같이 분포가 크게 변하는 경우 학습을 다시해야 하는 상황에 놓이거나 학습하는 과정을 어렵게 만들 수 있다. 이러한 상황에서 $\beta$와 $\gamma$를 이용해 입력값들을 통제한다면 일관된 분포의 예제들로 학습을 할 수 있기 때문에 수월하게 학습을 할 수 있게 된다.

위의 그림을 살펴보면 첫번째 은닉층을 하나의 입력값으로 살펴볼 때, 정규화를 통해서 각 층에 해당하는 예제들의 분포를 $\beta$와 $\gamma$를 바탕으로 통일 시킬 수 있게 된다. 이러한 과정을 각 층에서 진행을 하게되면 학습의 전 과정에서 일관된 형식의 데이터를 통해 학습을 진행할 수 있게되며 이는 학습의 속도를 보다 빠르게 한다.

Additianal Effects

---

일반적인 회기값을 이용하는 것이 아닌 $\tilde{z}$를 이용하는 것은 미니배치로 학습이 되는 신경망 입장에서 잡음(noise)로 해석 될 수 있다. 이는 각 은닉층에서 적용되는 것으로 각 층마다 잡음을 추가하는 것은 dropout 방식에서 시도하는 일반화 과정과 유사하다는 것을 볼 수 있다.

Reference

• Normalized shape