Residual Network

깊은 신경망은 복잡한 결정을 하는데 도움을 주는 것으로 알려져 있다. 하지만 실제로 신경망이 매우 깊어질 경우 미분값이 0으로 수렵하거나 값이 극도로 커지는 현상이 발생하여 학습 과정을 느리게 지연시킨다.

Building Residual Block

---

위의 그림과 같이 지름길(skip connection)을 만들어서 활성함수를 적용해 준다. 이러한 현태의 잔여 블록을 쌓음으로써 깊은 신경망을 만들 수 있다. 잔여 블록을 사용할 경우 항등함수의 학습이 매우 용이해진다. 이는 잔여 블록을 추가하여 학습 예제들의 수행 능력을 저하시키는 위험을 줄일 수 있다.

위의 수식을 보게되면 $g$가 항등함수일 때, 가중치와 오차값이 모두 0인 것을 볼 수 있다. 이는 항등함수에 대한 학습의 용이가 매우 쉬워진다는 장점이 존재한다. 항등함수에 대한 학습을 용이하게 하는 것은 미분값이 사라지는 문제(vanishing gradient)를 해결하는데 도움을 준다는 장점이 있다.

Identity Block

동일 블록은 잔여 신경망에서 가장 일반적으로 사용되는 종류로 건너뛰는 층의 값을 $n$이라고 할때, $a[l]$과 $a[l+n]$이 같은 차원을 가지는 것ㅇ르 의미한다. 잔여 블록이 합쳐지는 순간은 두번째 층의 활성함수를 적용하기 전이다.

1. First component
   • Conv2D, $F_1$ filters of shape (1,1), stride of (1,1), valid padding
   • Batchnormalization at channel axis
   • apply ReLU activation function
2. Second component
   • Conv2D, $F_2$ filters of shape (f,f), stride of (1,1), same padding
   • Batchnormalization at channel axis
   • apply ReLU activation function
3. Third component
   • Conv2D, $F_2$ filters of shape (f,f), stride of (1,1), same padding
   • Batchnormalization at channel axis
4. Final step
   • X + X_shortcut
   • apply ReLU activation function

def identity_block(X, f, filters, training=True, initializer=random_uniform):
    # Retrieve Filters
    F1, F2, F3 = filters
    
    X_shortcut = X
    
    # First
    X = Conv2D(filters=F1, kernel_size=1, strides=(1,1), padding='valid')(X)
    X = BatchNormalization(axis = 3)(X, training = training) # Default axis
    X = Activation('relu')(X)
    
    ## Second
    X = Conv2D(filters=F2, kernel_size=f, strides=(1, 1), padding='same')(X)
    X = BatchNormalization(axis=3)(X, training =training)
    X = Activation('relu')(X)

    # Third 
    X = Conv2D(filters=F3, kernel_size=1, strides=(1, 1), padding='valid')(X)
    X = BatchNormalization(axis=3)(X, training=training)
    
    # Final 
    X = Add()([X, X_shortcut])
    X = Activation('relu')(X)

    return X

Convolutional block

지름길을 통해 더해지는 활성화 값에 합성곱 층을 적용하여 잔여 블록을 만드는 방식이다. 기본적으로 차원이 다르기 때문에 차원을 맞춰주는 과정이 필요한데 이를 합성곱 연산을 이용한다. 그렇기 때문에 활성함수는 적용하지 않는다.

위의 $W_s$의 역할과 비슷한 역할을 합성곱 층이 해주고 있는 모습이다. 합성곱을 통해서 차원을 줄여서 지름길을 통해 활성함수를 적용하기 전에 더해준다.

def convolutional_block(X, f, filters, s = 2, training=True, initializer=glorot_uniform):
    
    F1, F2, F3 = filters
    X_shortcut = X
    
    # First
    X = Conv2D(filters=F1, kernel_size=1, strides = (s, s), padding='valid')(X)
    X = BatchNormalization(axis=3)(X, training=training)
    X = Activation('relu')(X)
    
    # Second
    X = Conv2D(filters=F2, kernel_size=f, strides=(1, 1), padding='same')(X)
    X = BatchNormalization(axis=3)(X, training=training)
    X = Activation('relu')(X)

    # Third
    X = Conv2D(filters=F3, kernel_size=1, strides=(1,1), padding='valid')(X)
    X = BatchNormalization(axis=3)(X, training=training)

    X_shortcut = Conv2D(filters=F3, kernel_size=1, strides=(s,s), padding='valid')(X_shortcut)
    X_shortcut = BatchNormalization(axis=3)(X_shortcut, training=training)

    # Final
    X = Add()([X, X_shortcut])
    X = Activation('relu')(X)
    
    return X

Building ResNet Model(ResNet50)

---

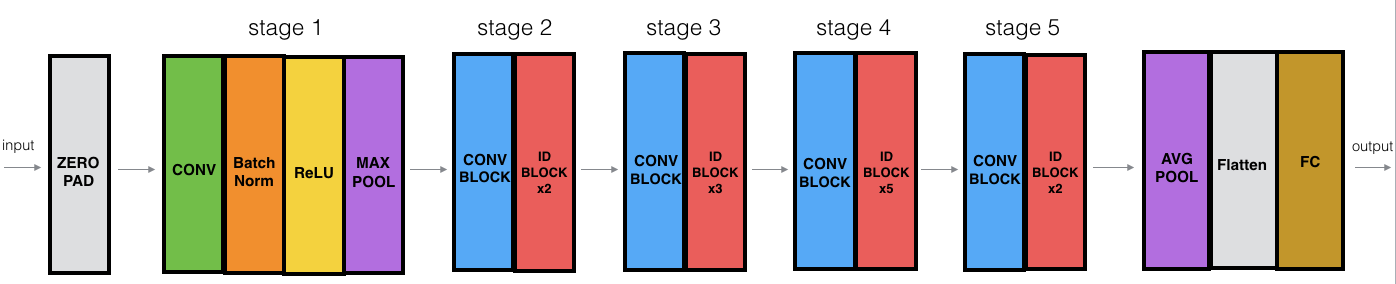층이 50개인 잔여 신경망을 만들어보도록 하자. 코드에서 특징적인 면은 동일 블록에서 필터의 채널이 두배씩 증가하는 것을 볼 수 있는데, VGG-16의 특징이 나타나있는 코드로 해석할 수 있을 것으로 보인다.

def ResNet50(input_shape = (64, 64, 3), classes = 6):
    X_input = Input(input_shape)

    # Zero-Padding
    X = ZeroPadding2D((3, 3))(X_input)
    
    # Stage 1
    X = Conv2D(64, (7, 7), strides = (2, 2))(X)
    X = BatchNormalization(axis = 3)(X)
    X = Activation('relu')(X)
    X = MaxPooling2D((3, 3), strides=(2, 2))(X)

    # Stage 2
    X = convolutional_block(X, f = 3, filters = [64, 64, 256], s = 1)
    X = identity_block(X, 3, [64, 64, 256])
    X = identity_block(X, 3, [64, 64, 256])

    # Stage 3
    X = convolutional_block(X, f = 3, filters = [128, 128, 512], s = 2)
    X = identity_block(X, 3, [128, 128, 512])
    X = identity_block(X, 3, [128, 128, 512])
    X = identity_block(X, 3, [128, 128, 512])
    
    # Stage 4
    X = convolutional_block(X, f = 3, filters = [256, 256, 1024], s = 2)
    X = identity_block(X, 3, [256, 256, 1024])
    X = identity_block(X, 3, [256, 256, 1024])
    X = identity_block(X, 3, [256, 256, 1024])
    X = identity_block(X, 3, [256, 256, 1024])
    X = identity_block(X, 3, [256, 256, 1024])

    # Stage 5
    X = convolutional_block(X, f = 3, filters = [512, 512, 2048], s = 2) 
    X = identity_block(X, 3, [512, 512, 2048])
    X = identity_block(X, 3, [512, 512, 2048])

    # AVGPOOL
    X = AveragePooling2D(pool_size=(2,2))(X)

    # output layer
    X = Flatten()(X)
    X = Dense(classes, activation='softmax')(X)

    # Create model
    model = Model(inputs = X_input, outputs = X)

    return model

Reference

• Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun - Deep Residual Learning for Image Recognition (2015)
• Francois Chollet's GitHub repository: https://github.com/fchollet/deep-learning-models/blob/master/resnet50.py