
Calib_cam_to_cam
Camera-to-camera calibration
- S_xx: 1x2 size of image xx before rectification
- K_xx: 3x3 calibration matrix of camera xx before rectification
- D_xx: 1x5 distortion vector of camera xx before rectification
- R_xx: 3x3 rotation matrix of camera xx (extrinsic)
- T_xx: 3x1 translation vector of camera xx (extrinsic)
- S_rect_xx: 1x2 size of image xx after rectification
- R_rect_xx: 3x3 rectifying rotation to make image planes co-planar
- P_rect_xx: 3x4 projection matrix after rectification
| 종류 | 형태 | 설명 |
|---|---|---|
| S[n] | 1 x 2 | original 이미지 사이즈 / 1392 X 512 이런식으로 |
| K[n] | 3 x 3 | calibration matrix / rectification 하기 전 |
| D[n] | 1 x 5 | 카메라의 distortion vector / rectification 하기 전 |
| R[n] | 3 x 3 | 카메라의 rotation matrix / velodyne → camera |
| t[n] | 3 x 1 | 카메라의 translation vector / velodyne → camera |
n = 0 : left gray
n = 1 : right gray
n = 2 : left color
n = 3 : right color
Rectification : 에피폴라 라인을 평행하도록 이미지를 변환하는 과정을 이미지 렉티피케이션
S[n]: 1x2 size of image [n] before rectification. (이미지 크기)
K[n]: 3x3 calibration matrix of camera [n] before rectification
D[n]: 1x5 distortion vector of camera [n] before rectification
R[n]: 3x3 rotation matrix of camera [n](extrinsic)
T[n]: 1x3 translation vector of camera [n] (extrinsic)
Srect[n]: 1x2 size of image [n] after rectification
Rrect[n]: 3x3 rectifying rotation to make image planes co-planar
Prect[n]: 3x4 projection matrix after rectification
P0, P1은 camera intrinsic 이 아님. projection matrix임
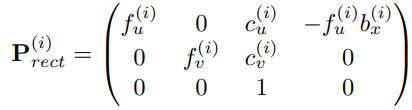
P1=calibration_matrix * [R_1 | T_1]
Tr → concatenation of all camera position → 12개의 element
| O O O | O O O | O O O | O O O |
|---|---|---|---|
| P0 | P1 | P2 | P3 |
Ref
As the transformations sometimes confuse people, here we give a short
example how points in the velodyne coordinate system can be transformed
into the camera left coordinate system.
In order to transform a homogeneous point X = [x y z 1]' from the velodyne
coordinate system to a homogeneous point Y = [u v 1]' on image plane of
camera xx, the following transformation has to be applied:
Y = P_rect_xx * R_rect_00 * (R|T)_velo_to_cam * X
To transform a point X from GPS/IMU coordinates to the image plane:
Y = P_rect_xx * R_rect_00 * (R|T)_velo_to_cam * (R|T)_imu_to_velo * X
Calib_velo_to_cam
velodyne to camera calibration
ex)
calib_time: 11-May-2999 10:10:10
R: 7.5e-03 -9.7e-01 -6.0e-04 1.4e-02 7.2e-04 -9.9e-01 3.9e-01 7.5e-03 1.5e-02
T: -4.6e-03 -7.8e-02 -2.6e-01
delta_f: 0.000000e+00 0.000000e+00
delta_c: 0.000000e+00 0.000000e+00
