Previous Lectures

Message Passing Neural Nets

• Node features are updated from iteration t to t+1 via learnable permutation invariant neighborhood aggregate AGG and update UPD

Graph Neural Networks

• Message passing updates node features using local aggregation
• stacking multiple graph neural network - expand perceptual fields...

Normal Graph Neural Networks

• Advanced GNN layers make pooling over node features, which are then used to make a graph-level prediction

Molecular Graphs

• Molecules can be represented as a graph G with node features $s_i$ and edge feature $a_{ij}$
  - Node features: atom type, atom charges
  • Edge features: valuence bond type
  • However,sometimes, we also know the 3D positions $x_i$, which is actually more informative

3D structure에 Graph를 어떻게 적용할 것인가?
small molecules, proteins, DNA/RNA, Inorganic Crystals, Catalysis Systems, Transportation & Logistics, Robotic Navigation ...

Geometric Graphs

• A geometric graph G = (A, S, X) is a graph where each node is embedded in d-dimensional Euclidean space.
  - A: Adjacency matrix
  • S: scalar features
  • X: tensor features

Broad Impact on Sciences

• Supervised Learning: Prediction
  - Properties predictions
  input: Geometric Graph → Geometric GNN → Output: Prediction
• Supervised Learning: Structured Prediction
  - Molecular Simulation
  input: current state → Geometric GNN + Dynamics Simulator → next state → ...
  분자의 안정 상태가 무엇인지를 simulate 하고 싶음. 어떻게 움직여야 하는지를 조금씩 움직여가면서 구한다.
• Generative Models
  - Drug or material design
  input: Geometric Graph → Geometric GNN + Generative Model → Geometric Graph

What's the obstacle?

• To describe geometric graphs we use coordinate systems
  - (1) and (2) use different coordinate systems to describe the same molecular geometry
• We can describe the transform between coordinate systems with symmetries of Euclidean space
  - 3D rotations, translations
• However, ouput of traditional GNNs given (1) and (2) as completely different!

Symmetry of Inputs

• We want our GNNs can see (1) and (2) as the same systems though described differently...
• i.e., we want design Geometric GNNs aware of symmetry!

Symmetry of Outputs

• Beyond input space, output can also be tensors
• Example: simulation (force prediction)
  - Given a molecule and a rotated copy, predicted forces should be the same up to rotation
  • i.e., Predicted forces are equivariant to rotation

Equivariance

• Formal definition of Equivariance:
  a function F: X→Y is equivariant if for a transformation p is satisfies:
  

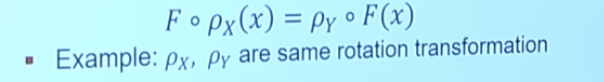
Illustration: 3D Rotation Equivariance

구조가 회전하면 힘 역시 같은 형식으로 변경되어야 한다.

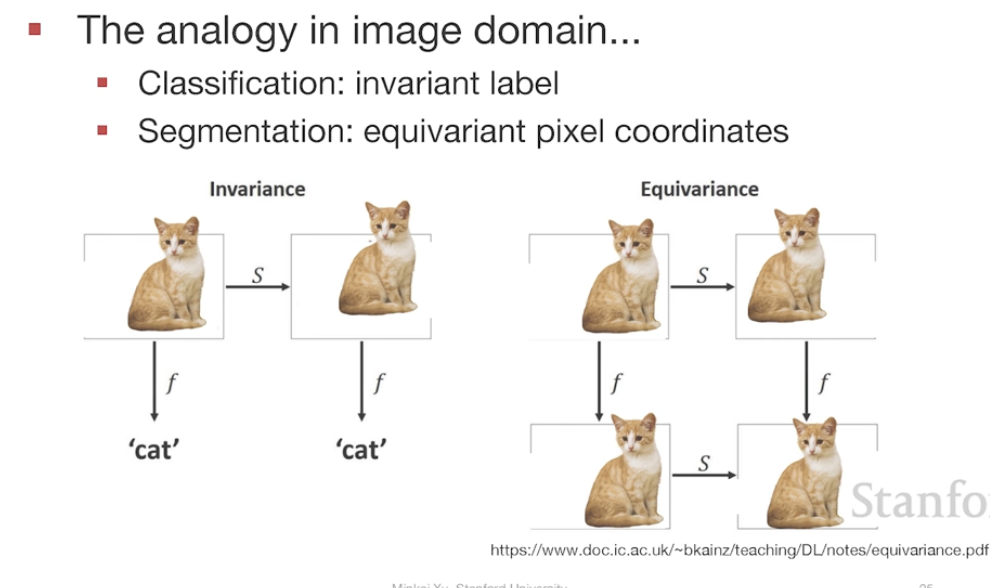
Invariance

• Definition of Invariance:
  a function F:X→Y is invariant if for a transformation p it satisfies:
  F * P_x(x) = F(x)
  어떤 회전을 하더라도 같은 예측을 해야 한다.
  Equivariance의 special case임

Invariance & Equivariance

• For geometric graphs, we consider 3D Special Euclidean (SE(3)) symmetries
  - Structure x → energy E: invariant scalars
  - Structure x → force v: equivalent tensors
  rotation equivariant and translation invariant
  

Geometric GNNs

Two classes of Geometric GNNs:

• Invariant GNNs for learning invariant scalar features
• Equivariant GNNs for learning equivalent tensor features

Molecular Dynamics Simulations

• For simulating the stable structure of molecular geometrics: computiationally costly quantum mechanical calculations

For ML Models...

atom types, positions를 바탕으로 energy나 forces를 예측하고 싶음

Invariant GNNs: SchNet

• SchNet updates the node embeddings at the lth layer by message passing layers
• Schnet makes W invariant by scalarizing relative positions $r_{ij}$ with relative distances
• Stack multiple interaction and atom-wise layers
• Predict single scalar value for each atom
• Sum all scalars together as energy prediction

Improved SchNet: DimeNet

• Chemcially, potential energy can be modeled as sum of four parts
• DimeNet resolves this problems by
  - Do message interaction based on
  1. Distance between atoms
  2. angle between bonds

Expressiveness

• Distances/Angles are imcomplete descriptors for uniquely identifying geometric structure
• This pair of geometric graphs cannot be distinguished by identical scalr quantities
• But they can be distinguished based on directional or geometric information

Equivariant GNNs: PaiNN

• PaiNN still take learnable weights W conditioned on the relative distance to control message passing
• However, differently, in PaiNN each node has two features (both scalar features $s_i$ and vector feature)

Molecular Conformation Generation

• Generate stable confroamtions from molecular graph

Challenges

• Generative models learns the data distribution
• Similar to the learning algorithm, geneartion process should also capture the physical symmetry groups., i.e., equiariant to roto-translation
• Diffusion model 사용 → Geometric Diffusion