Message Passing and Node Classification

Outline

• Main Question: Given a network with labels on some nodes, how do we assign labels to all other nodes in the network?
• Example: In a network, some nodes are fraudsters and some other nodes are fully trusted. How do you find the other fraudsters and trustworthy nodes?
• We already discussed node embeddings as a method to solve this in Lecture 3 (노드 임베딩을 사용하여 trust/not trust를 판별하는 classifer를 생성)

Example: Node Classification

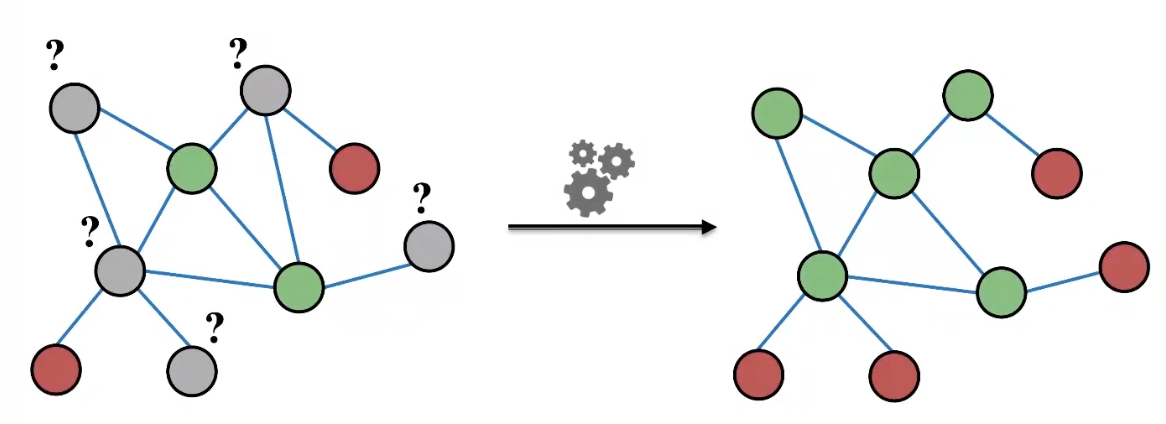
• Given labels of some nodes

• Let's predict labels of unlabeled nodes

• This is called semi-supervised node classification

• Today we will discuss an alternative framework:
  Message Passing

• Intuition: Correlations exist in neworks.
  - In other words: Similar nodes are connected

  • Key concept is collective classificaton: Idea of assigning labels to all nodes in a network together

• We will look at three techniques today:
  - Relational classification

  • Iterative classification
  • Belief propagation

Correlations Exists in Networks

• Indicidual behaviors are correlated in the network
• Correlation: nearby nodes have the same color (belonging to the same class)
• Main types of dependencies that lead to correlation:
  

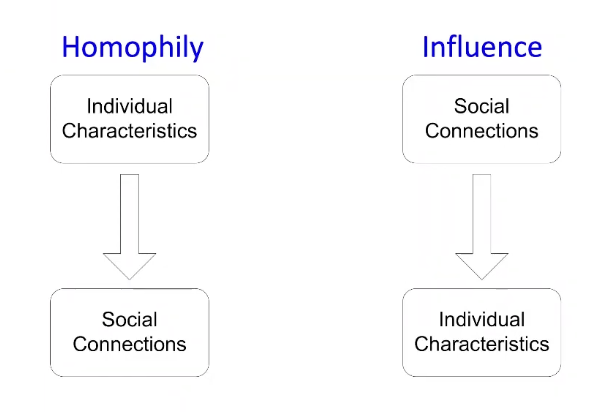
Homophily

• Homophily : The tendency of individuals to associate and bond with similar others
  - "Birds of a feather flock together"
  • It has been observed in a vast array of network studies, based on a variety of attributes (e.g., age, gender, organizational role, etc.)
  • Example: Researchers who focus on the same research area are more likely to establish a connection (meeting at conferences, interacting in academic talks, etc.)

Influence

• Influence : Social connections can influence the individual characteristics of a person
  - Example: I recommend my musical preferences to my friends, until one of them grows to like my same favorite genres!

Classification with Network Data

• How do we leverage this correlation observed in networks to help predict node lables?
  
  How do we predict gray nodes?

Motivation (1)

• Similar nodes are typically close together or directly connected in the network:
  - Guilt-by-assoication: If I am connected to a node with label X, then I am liekly to have label X as well
  • Exmaple: Malicious/begign web page:
    Malicious web pages link to one another to increase visibility, look credible, and rank higher in search engines

Motivation (2)

• Classification label of a node v is network may depend on
  - Features of v
  • Labels of the nodes in v's neighborhood
  • Features of the nodes in v's neighborhood

Semi-supervised Learning

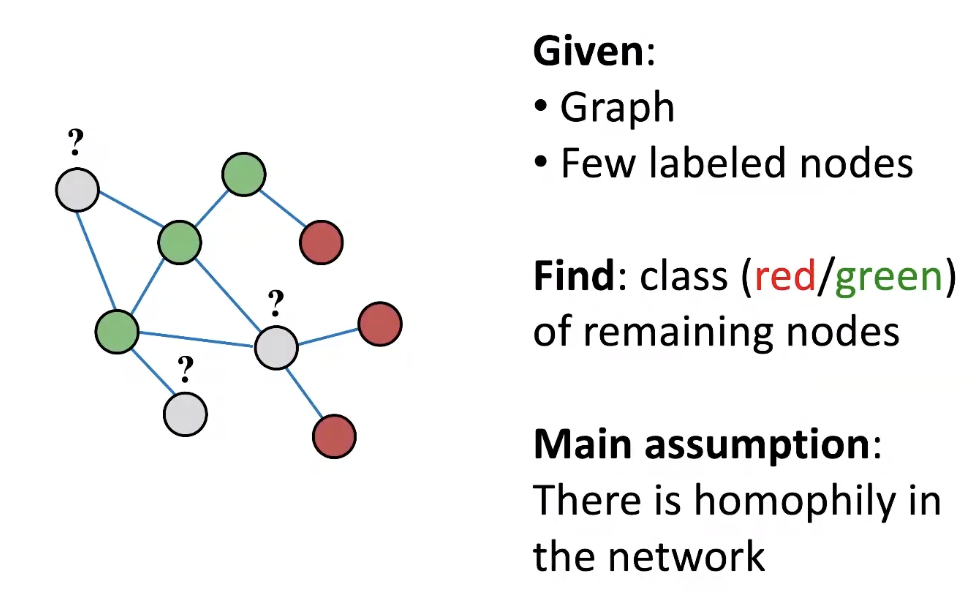
network 안에 homophily가 있음을 가정한다.
Example Task

• Let A be a nxn adjacency matrix over n nodes
• Let Y = {0, 1}^n be a vector of labels
  - $Y_v$ = 1 belongs to class 1
  • $Y_v$ = 0 belongs to class 0
  • There are unlabeled node needs to be classified
• Goal: Predict which unlabeled nodes are likely class 1, and which are likely class 0 (라벨링이 되지 않은 노드들이 class 1 인지 class 0인지를 예측하는 task)

Approach: Collective Classification

• Many applications:
  - Document classification
  • Part of speech tagging
  • Link prediction
  • Optical character recognition
  • Image/3D data segmentation
  • Entity resoultion in sensor networks
  • Spam and fraud detection

Collective Classification Overview

• Intuition: Simultaneous classification of interlinked nodes using correlations
• Probabilistic framework
• Markov Assumption: the label $Y_v$ of one node v depends on the labels of its neighbors $N_v$
  $P(Y_v) = P(Y_v|N_v)$
• Collective classification involves 3 steps

1. Local Classifier: Assign initial labels, Used for initial label assignment

• Predicts labels based on node attributes/features
• Standard classification task
• Does not use network information

2. Relational Classifier: Capture correlations between nodes

• Learns a classifier to label one node based on the labels and/or attributes of its neighbors
• This is where network information is used

3. Collective Inference: Propagate correlations through network

• Apply relational classifier to each node iteratively
• Iterate until the inconsistency between neighboring labels is minimized
• Network structure affects the final prediction

Problem Setting

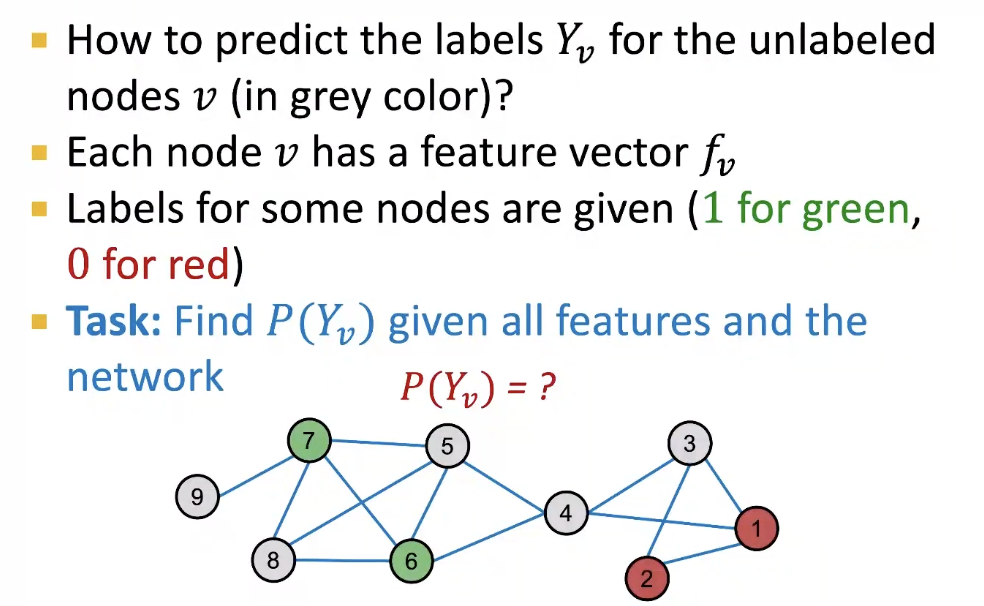
각 node가 class에 포함될 확률을 구하기

Relational and Iterative Classification

Probabilistic Relational Classifier

• Basic idea: Class probability $Y_v$ of node v is a weighted average of class probabilities of its neighbors
• For labeled nodes v, initialize label $Y_v$ with ground-truth label $Y_v^*$
• For unlabeled nodes, initalize $Y_v$ = 0.5
• Update all nodes in a random order until convergence or until maximum number of iteration is reached
• Update for each node v and label c
  
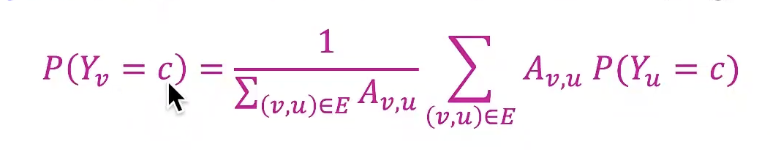
  - If edges have strength/weight information, $A_{v, u}$ can be the edge weight between v and u (A의 구조에 따라서 update가 달라진다)
  - $P(Y_v=c)$ is the probability of node c having label c
• Challenges:
  - Convergence is not guaranteed
  • Model cannot use node feature information

Example: Initialization

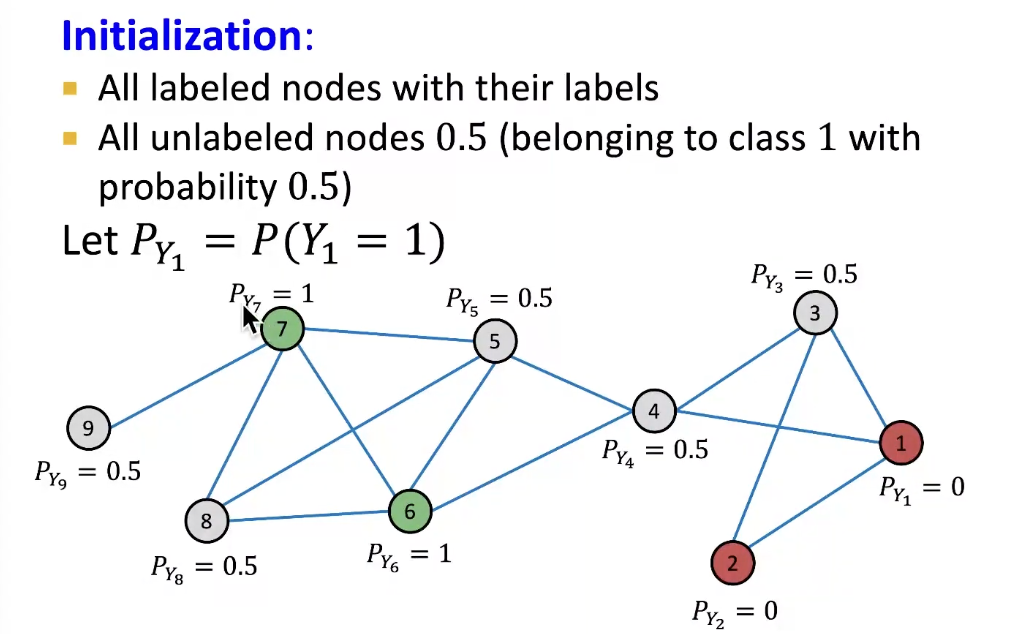
• 1st iteration, Update Node 3
  

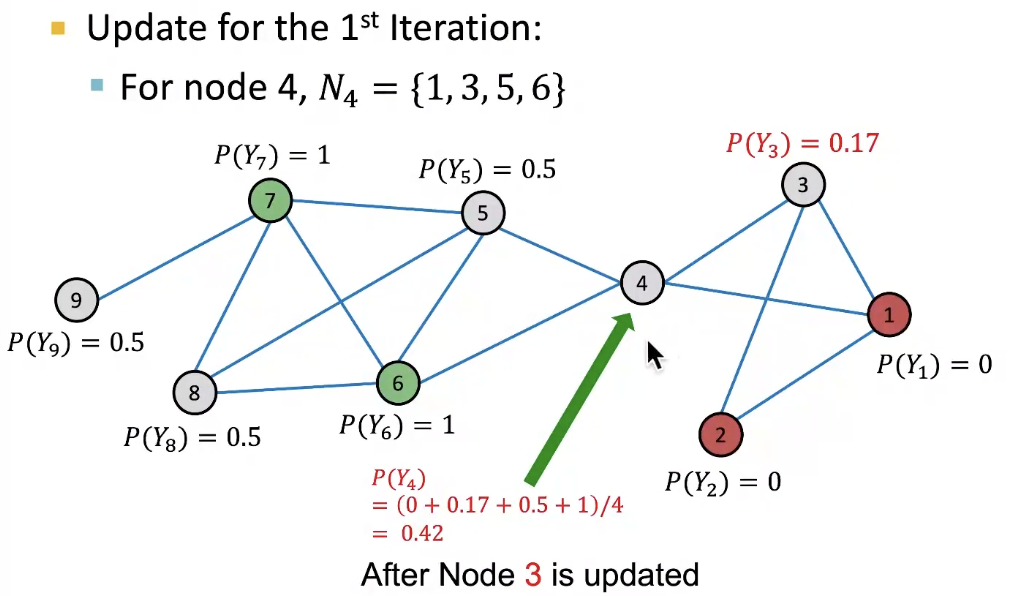
• After 1st iteration
  

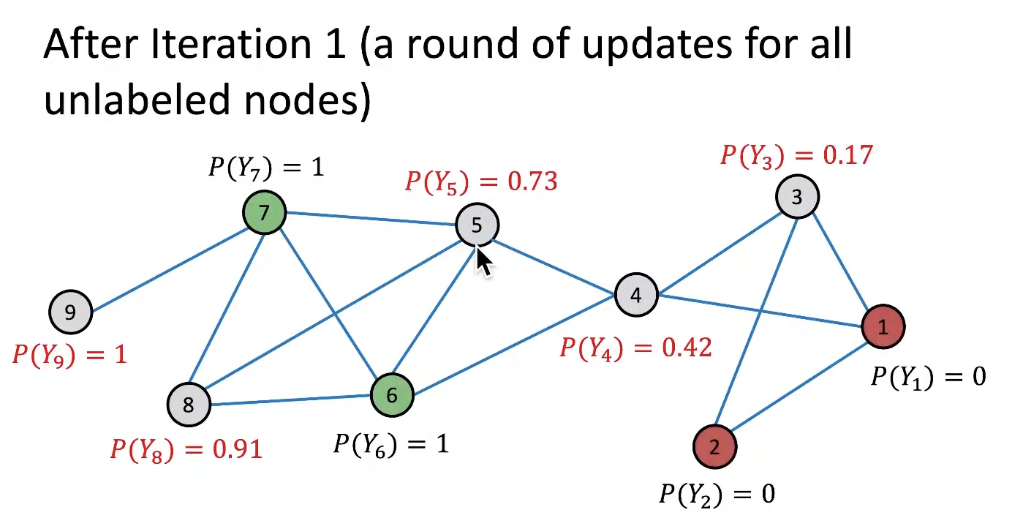
• and so on...

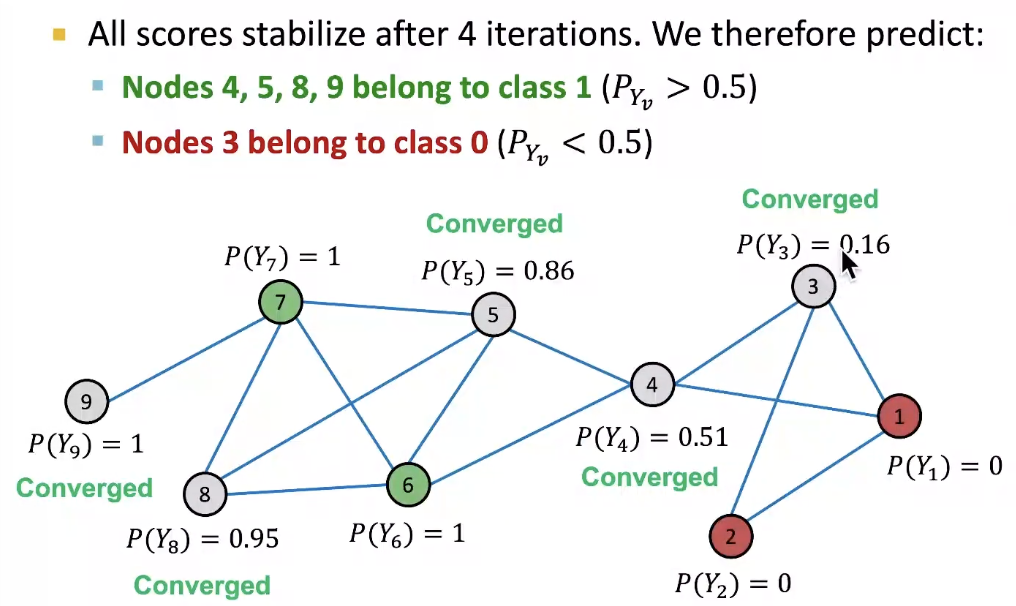
• Convergence
  각 prediction 확률의 값에 따라서 classification을 진행한다.
  

Iterative Classification

• Relational classifier do not use node attributes. How can one leverage them?
• Main idea of iterative classification: Classify node v based on its attributes $f_v$ as well as labels $z_v$ of neighor set $N_v$
• Input: Graph
  - $f_v$: feature vector for node v
  • Some nodes v are labeled with $Y_v$
• Task: Predict label of unlabeled nodes
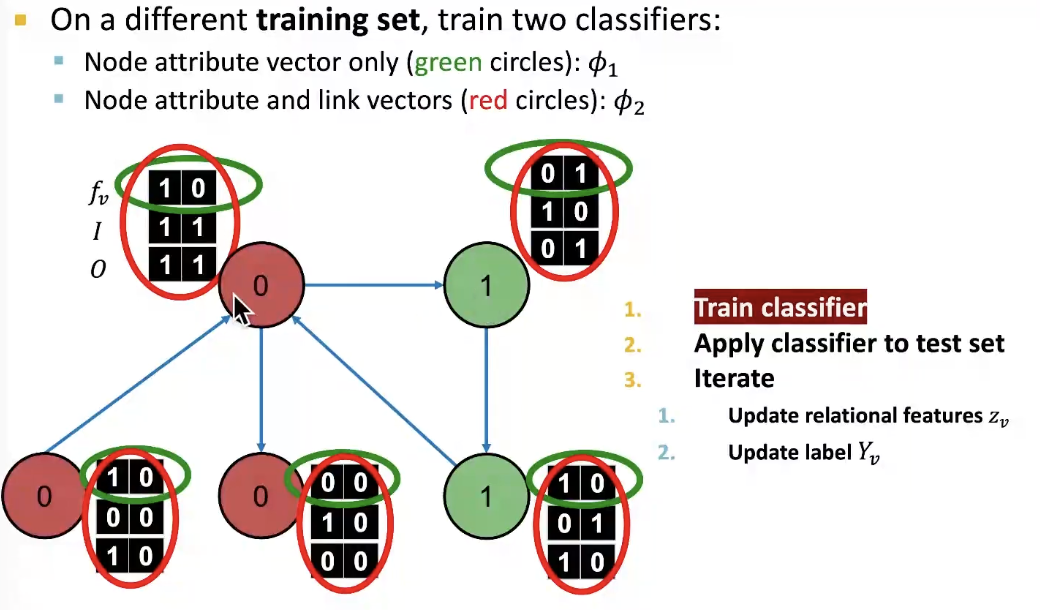
• Approach: Train two classifiers:
  
  node의 feature vector만을 사용해서 예측하는 classifer 1
  node의 feature와 주변의 label을 요약한 feature 정보로 예측하는 classifier 2

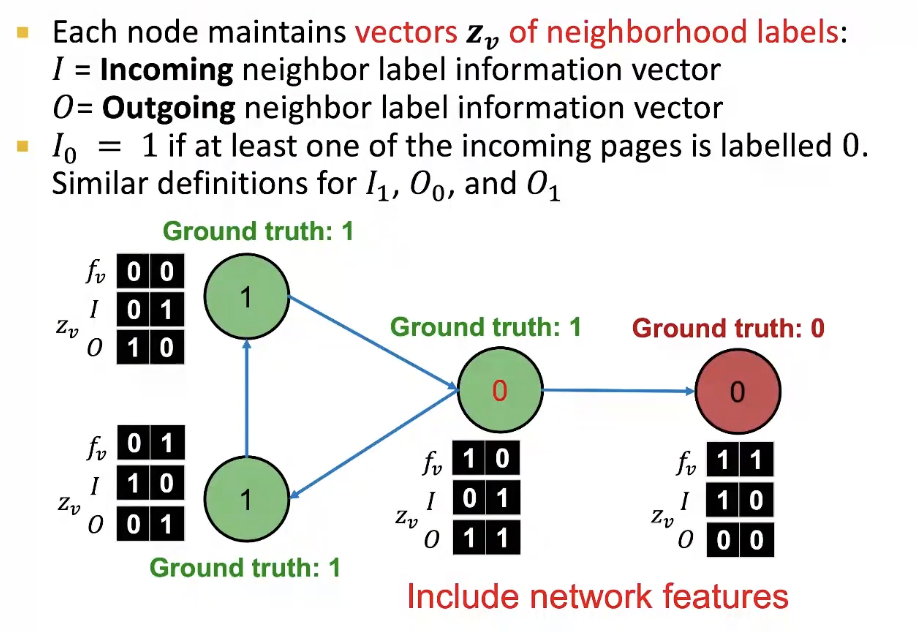
Computing the Summary $Z_v$

주변의 정보를 한 번에 모으는 과정을 어떻게 하는가?

• Ideas: $z_v$ = vector
  - Histogram of the number (or fraction) of each label in %N_v$
  • Most common label in $N_v$
  • Number of different labels in $N_v$

Architecture of Iterative Classifiers

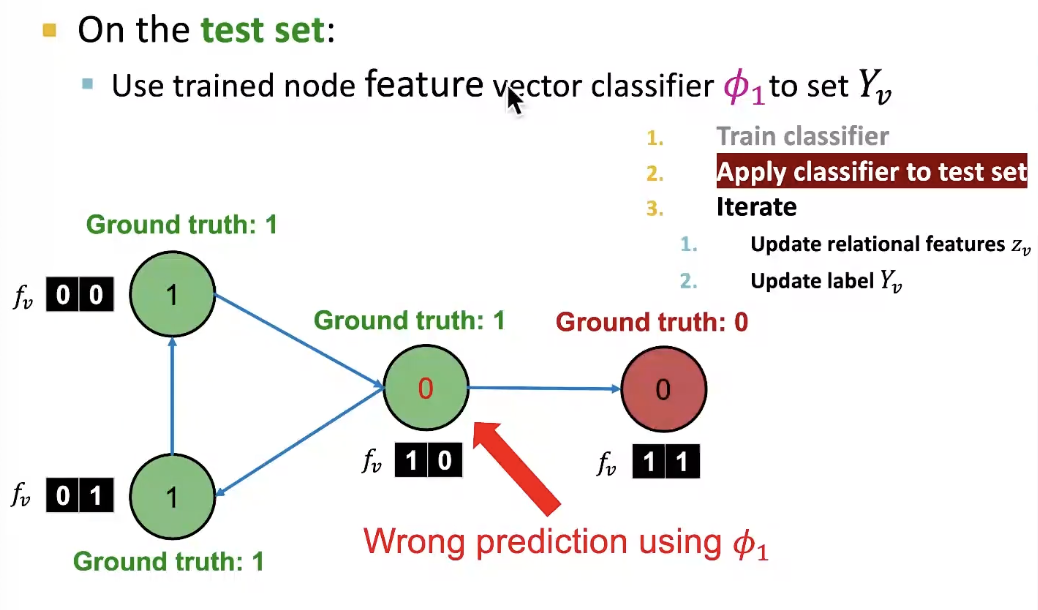
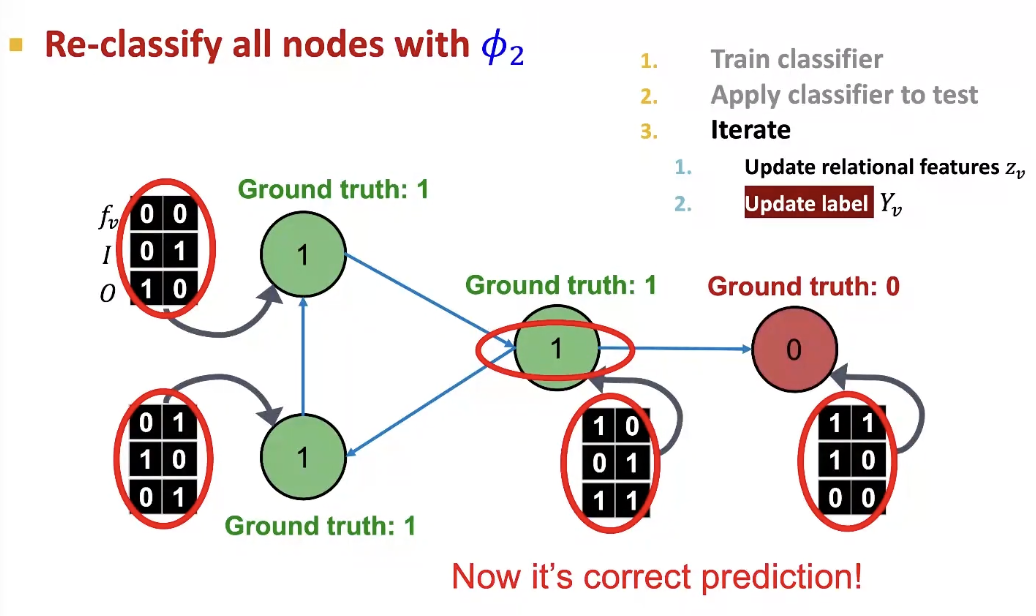
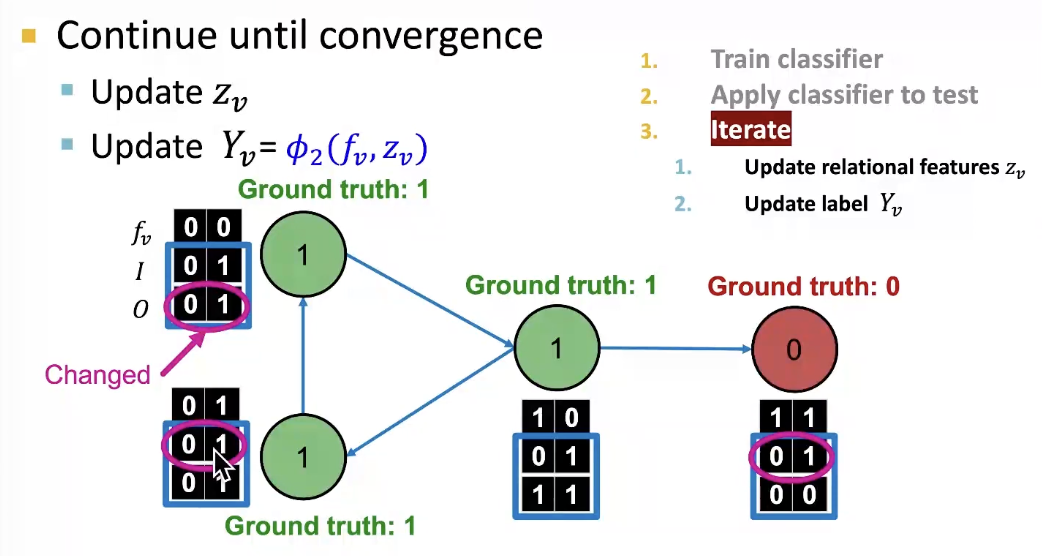
• Phase 1: Classify based on node attributes alone
  
• Phase 2: Iterate till convergence
  

Example: Web Page Classification

• Input: Graph of web pages
• Node: Web page
• Edge: Hyper-link between web pages
  - Directed edge: a page points to another page
• Node features: Webpage description
  - For simplicity, we only consider 2 binary features
• Task: Predict the topic of the webpage
• Baseline: Train a classifier to classify pages based on binary node attributes
  
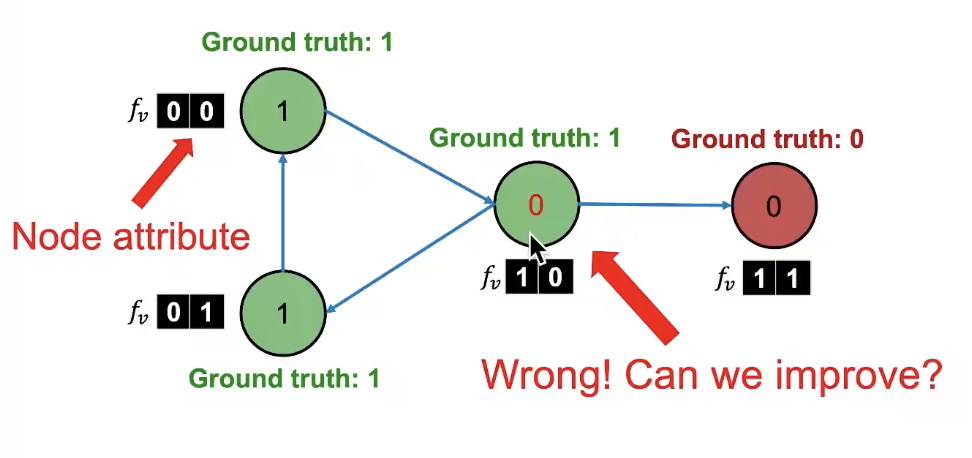
  노드의 색이 ground-truth임
  
  Iterative Classifer - Step1
  
  Iterative Classifer - Step2
  
  Iterative Classifer - Step3
  
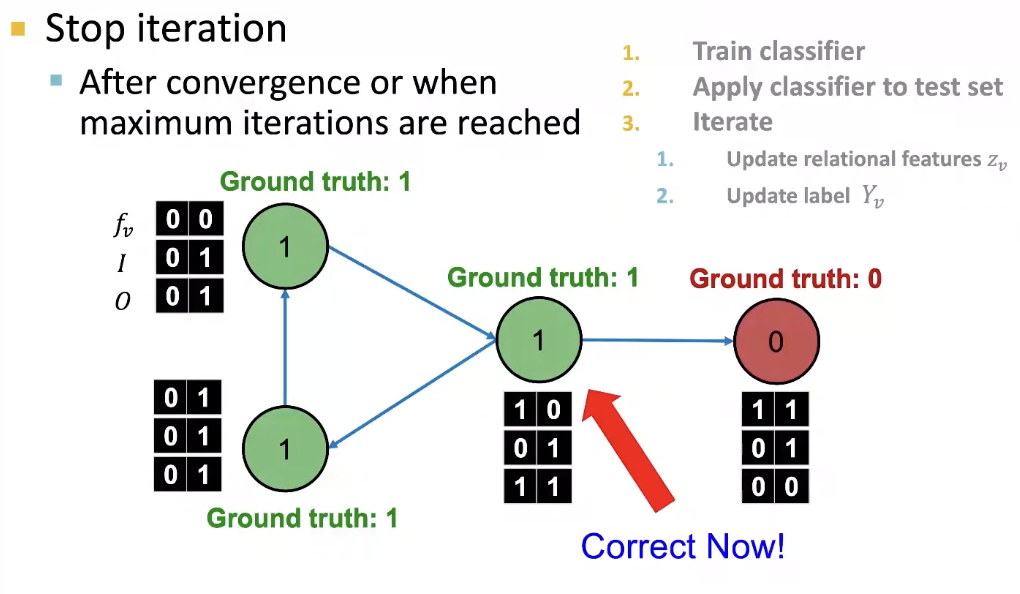
  Iterate
  
  Final Prediction
  

Collective Classification: Belief Propagation

Loopy Belief Propagation

• Belief Propagation is a dynamic programming approach to answering probability queries in a graph
• Iterative process in which neighbor nodes "talk" to each other, passing messages
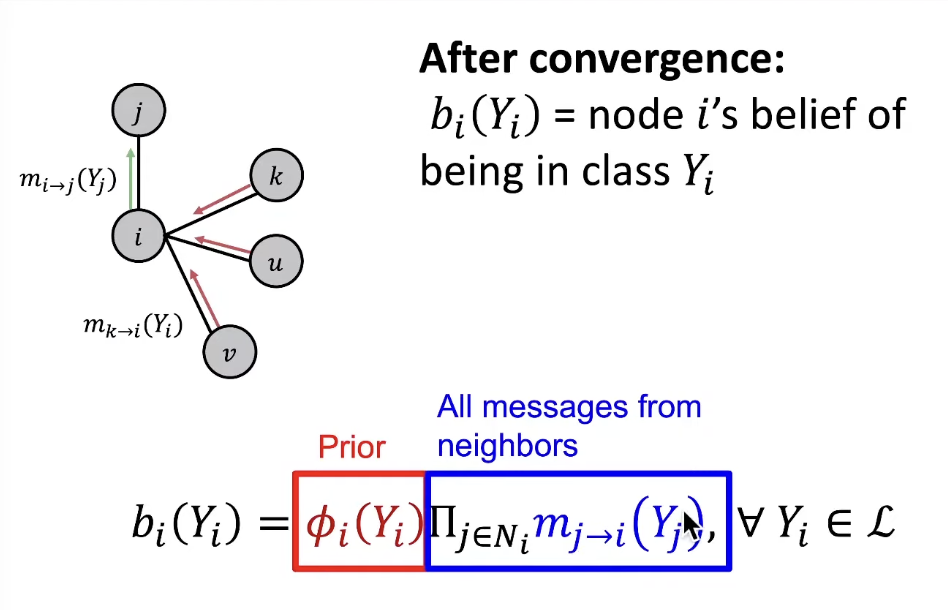
• When consensus is reached, calculate final belief

Message Passing: Basics

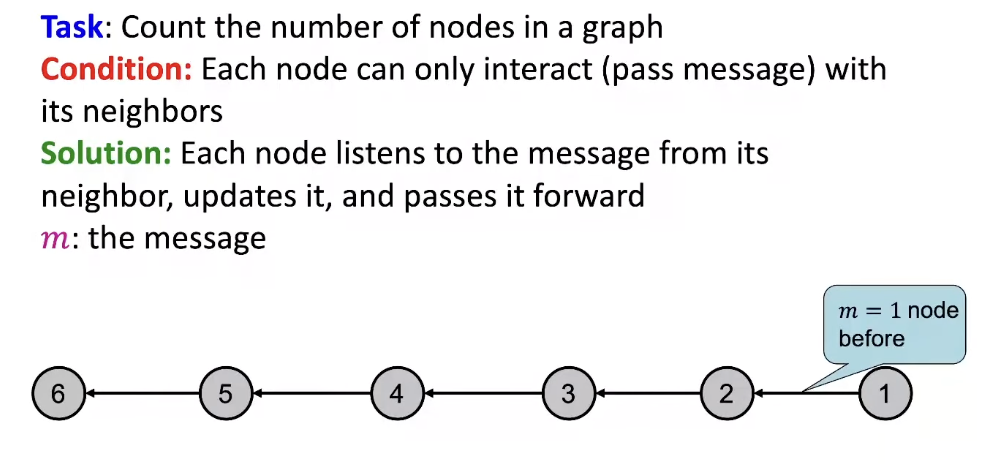
• Task: Count the number of nodes in a graph
• Condition: Each node can only interact (pass message) with its neighbors
• Example: path graph
  

Message Passing: Algorithm

• Task: Count the number of nodes in a graph
• Algorithm
  - Define an ordering of nodes (that results in a path)
  • Edge directions are according to order of nodes
    • Edge direction defines the order of message passing
  • For node i from 1 from 6
    • Compute the message from node i to i+1 (number of nodes counted so far)
      Pass the message from. node i to i+1

Generalizing to a Tree

• We can perform message passing not only on a path graph, but alos on a tree-structured graph
• Define order of message passing from leaves to root

Loopy BP Algorithm

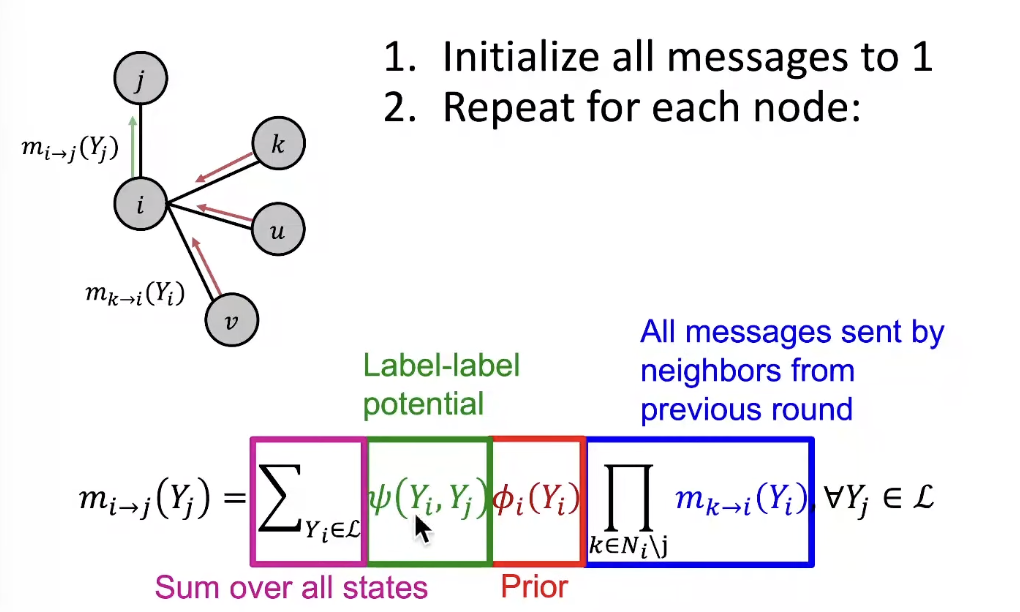
What message will i send to j?

• It depends on what i hears from its neighbors
• Each neighbor passes a message to i its beliefs of the state of i

Notation

• Label-label potential matrix
• Prior belief
  

Loopy Belief Propagation

• Now we consider a graph with cycles
• There is no longer an ordering of nodes
• We apply the same algorithm as in previous slides:
  - Start from arbitrary nodes
  • Follow the edges to update the neighboring nodes
• 만약 graph에 cycle이 존재한다면? no longer independent!!!!, 알고리즘을 적용할 수는 있으나 메세지가 cycle 안에 돌고 돌 것이다.

What Can Go Wrong?

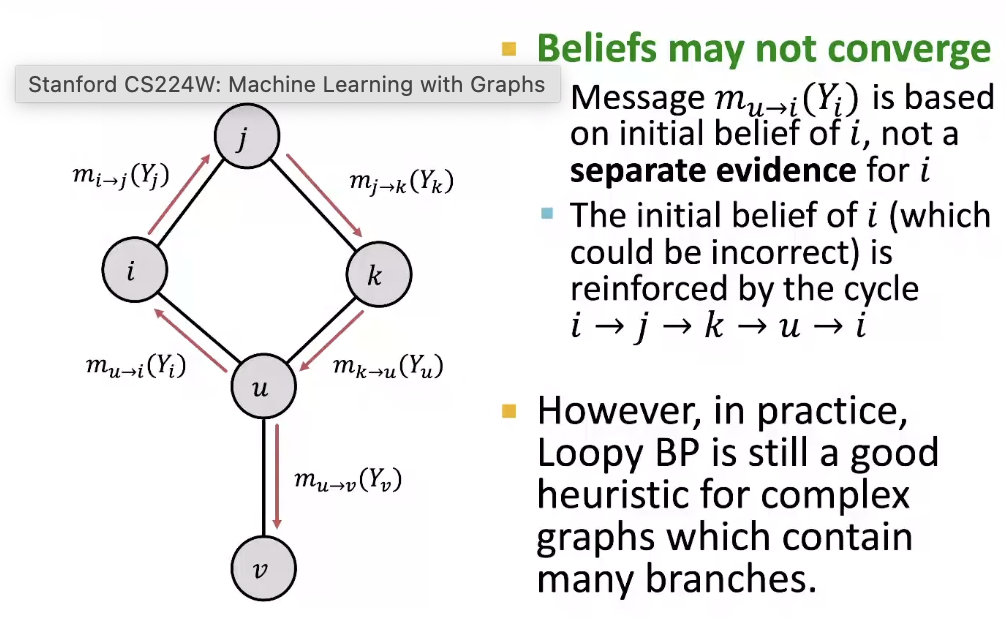
Advantages of Belief Propagation

• Advantages
  - Easy to program & parallelize
  • General: can apply to any graph model with any form of potentials
    • Potential can be higher order
• Challenges
  - Convergence is not guaranteed (when to stop), especially if many closed loops
• Potential functions (parameters)
  -Require training to estimate