Graph as Matrix: PageRank, Random Walks and Embeddings

Graph as Matrix

• We investigate graph analysis and learning from a matrix perspective.
• Treating a graph as matix allows us to:
  ❍ Determine node importance via random walk (PageRank)
  ❍ Obtain node embeddings via matrix factorization (MF)
  ❍ View other node embeddings (e.g. Node2Vec) as MF
• Random walk, matrix factorization and node embeddings are closely related!

PageRank

Example: The Web as a Graph

Q: What does the Web "look like" at a global level?

• Web as graph
  
  information → graph 형태로

Ranking Nodes on the graph

• All web pages are not equally "important"
• There is large diversity in the web-graph node connectivity.
• So, let's rank the pages using the web graph link structure!

Link Analysis Algorithms

• We will cover the following Link Analysis approaches to compute the importance of nodes in a graph
  ❍ PageRank
  ❍ Personalized PageRank (PPR)
  ❍ Random Walk with Restarts

Links as Votes

• Idea: Links as Votes
  ❍ Page is more important if it has more links ; In-coming links? Out-going links?
• Think of in-links as votes
• Are all in-links equal?
  ❍ Links from important pages count more
  ❍ Recursive question!

PageRank: The "Flow" Model

• A "vote" from an important page is worth more:
  ❍ Each link's vote is proportional to the importance of its source page
  ❍ If page i with importance r_i has d_i out_links, each link gets r_i/d_i votes
  ❍ Page j's own importance r_j is the sum of the votes on its in-links
• A page is important if it is pointed to by other important pages
• Define "rank" r_j for node j
  

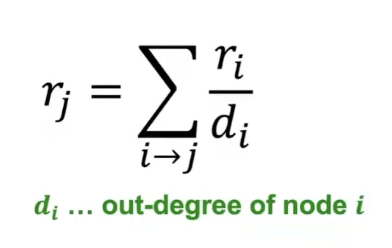
PageRank: Matrix Formulation

• Stochastic adjacency matrix M
  ❍ Let page j have d_j out_links
  ❍ If j → i, then M_ij = 1 / d_j (M: column stochastic matrix)
• Rank vector r: An entry per page
  ❍ r_i is the importance source of page i
• The flow equations can be written

Connection to Random Walk

• Imagine a random web surfer:
  ❍ At any time t. surfer is on some page i
  ❍ At time t+1, the surfer follows an out-link from i uniformly at random
  ❍ Ends up on some page j linked from i
  ❍ Process repeats indefinitely
• Let:
  ❍ p(t) ... vector whose ith cordinate is the prob. that the surfer is at page i at time t
  ❍ so, p(t) is a probability distribution over Given a pages

The Stationary distribution

• Where is the surfer at time t_1?
  ❍ Follow a link uniformly at random
  p(t+1) = M p(t)
  ❍ Suppose the random walk reaches a state
  p(t+1) = M p(t) = p(t)
  then p(t) is stationary distribution of a random walk
  ❍ Our original rank vector r satifies r = M * r (so, r is a stationary distribution for the random walk)

Eigenvector Formulation

PageRank: How to solve?

Given a graph with n nodes, we use an iterative procedure:

Power Iteration Method

• Given a web graph with N nodes, where the nodes are pages and edges are hyperlinks
• Power iteration: a simple iterative scheme
  

PageRank: How to solve?

Look careful of Power Iteration part

PageRank: Three Questions

• Does this converge?
• Does it converge to what we want?
• Are results reasonable?

PageRank: Problems

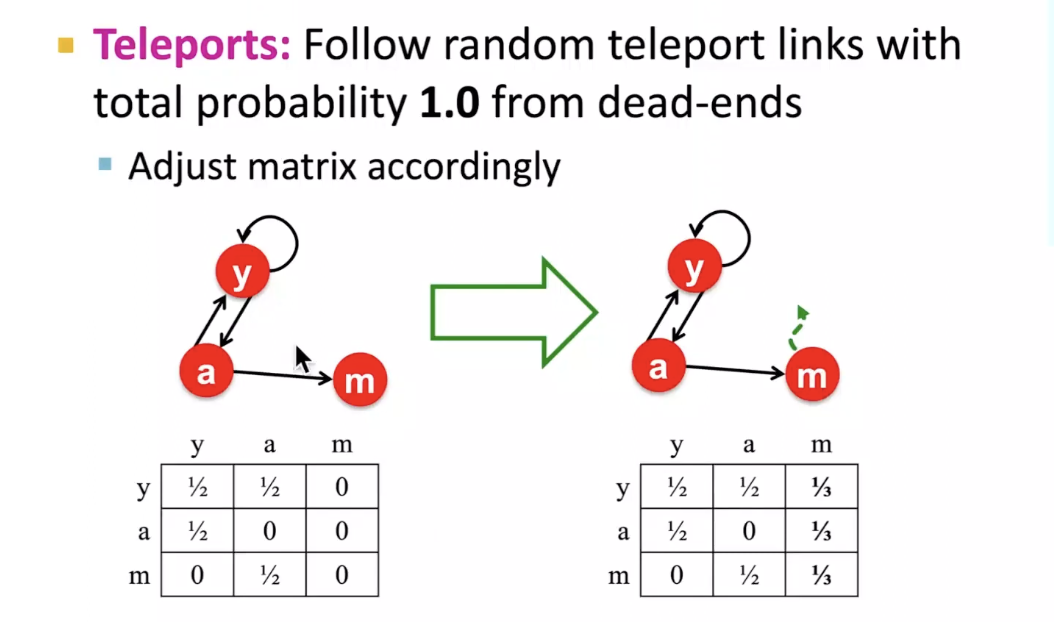
1. Some pages are dead ends (have no out-links)

• Such pages cause importance to "leak out"

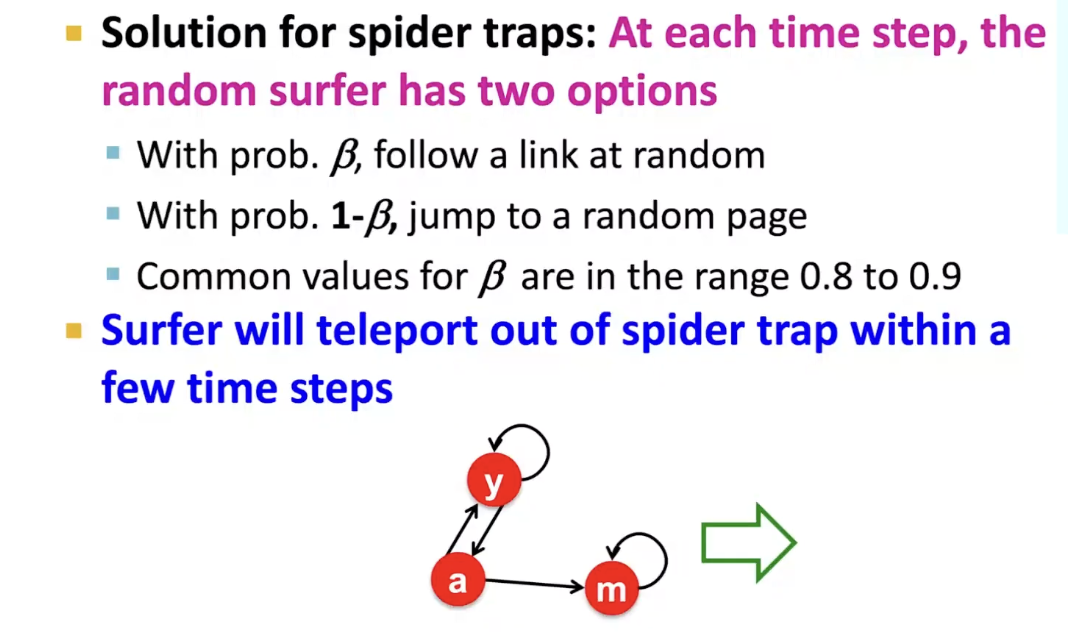
2. Spider traps (all out-links are within the group)

• Eventually spider traps abosrb all importance

Solution to Spider Traps

Solution to Dead Ends

Why Teleports Solve the Problem?

Why are dead-ends and spider traps a problem and why teleports solve the problem?

• Spider-traps are not a problem, but with traps PageRank scores are not what we want
  ❍ Soultion: Never get stuck in a spider trap by teleporting out of it in a finite number of steps
• Dead-ends are a problem
  ❍ The matrix is not column stochastic so our initial assumptions are not met
  ❍ Soultion: Make matrix column stochastic by always teleporting when there is nowhere else to go

Soultion: Random Teleports

Google matrix

Random Walk with Restarts and Personalized PageRank

Example: Recommendation

Bipartite User-Item Graph

Proximity on Graphs

• PageRank
  ❍ Ranks nodes by "importance"
  ❍ Teleports with uniform probability to any node in the network
• Personalized PageRank
  ❍ Ranks proximity of nodes to the teleport nodes S
• Proximity on graphs:
  ❍ Q: What is most related item to Item Q?
  ❍ Random Walks with Restarts

Idea: Random Walks

Benefits

• "similarity" considers
  ❍ Multiple connections
  ❍ Multiple paths
  ❍ Direct and indirect connections
  ❍ Degree of the node

Matrix Factorization and Node Embeddings

Connection to Matrix Factorization

• Simplest node similarity: Nodes u, v are similar if they are connected by an edge
  

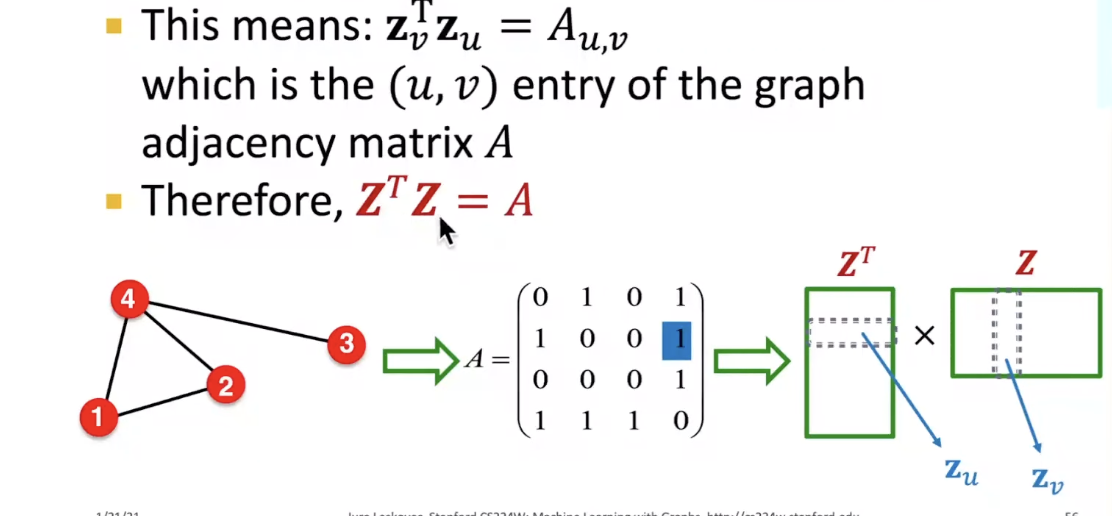
Matrix Factorization

Random Walk-based Similarity

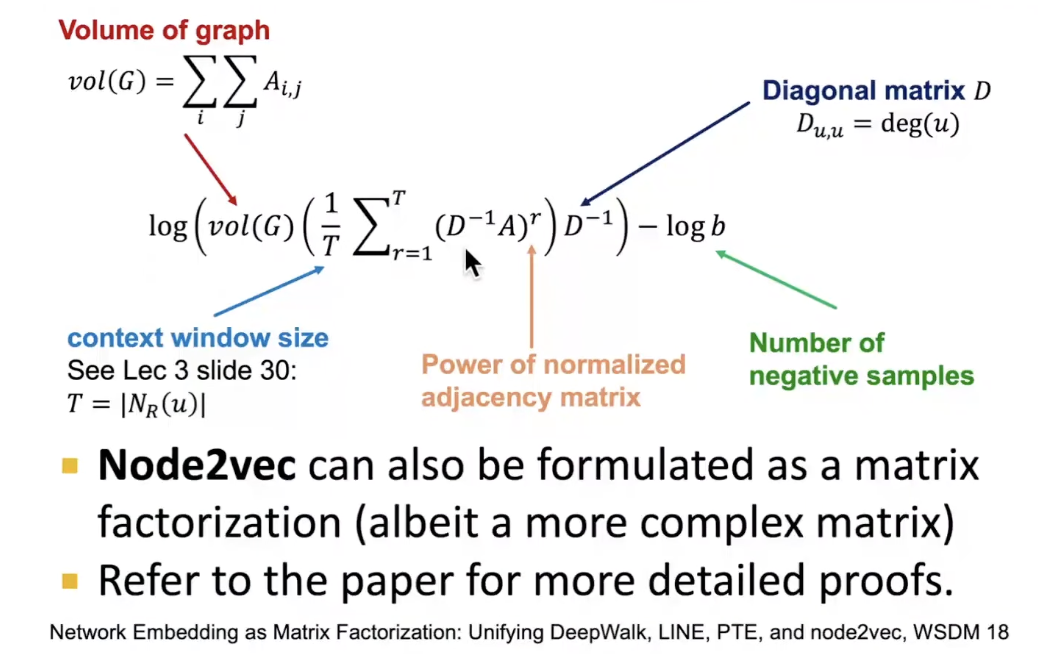
Limitations

1. Limitations of node embeddings via matrix factorization and random wlaks

• cannot obtain embeddings for nodes not in the training set

2. Cannot capture structural similarity

• DeepWalk and node2vec do not capture structural similarity

3. Cannot utilize node, edge and graph features