1. Introduction

• 훈련 데이터의 한계가 모델 확장에 어떤 영향을 미칠 수 있는가
• 모델 규모와 데이터 확장의 동향: 현재 언어 모델을 확장하는 추세는 모델의 매개변수 수와 훈련 데이터셋 크기를 동시에 증가시키는 방향으로 진행되고 있음. 이런 추세가 계속될 경우, 인터넷에 존재하는 텍스트 데이터의 양이 곧 한계에 도달할 수 있음 (What should we do when we run out of data?)
• 데이터 제약 상황에서의 모델 훈련: 텍스트 데이터의 한계에 도달하게 되면, 데이터 제약이 있는 상황에서 언어 모델을 어떻게 확장할 수 있을지가 중요한 연구 주제가 된다. 이 연구에서는 특히 데이터 반복 사용과 이가 모델 확장에 미치는 영향을 실험적으로 조사한다.
• 이전 연구: 많은 LLM들은 유니크 데이터를 사용해 단 한 번의 epoch으로 훈련되었음. 그러나 이 연구에서는 데이터를 반복해서 사용할 경우, 즉 여러 에포크에 걸쳐 같은 데이터를 사용할 경우의 효과를 분석한다. 이 연구는 반복 학습이 유효할 수 있음을 보여준다.
• 연구 목표: 데이터 제약 조건에서 언어 모델을 확장하는 최적의 방법을 찾는 것. 이를 위해 다양한 데이터 / 컴퓨팅 제약 하에서 400개 이상의 모델을 훈련시키고, 최종 테스트 손실을 기록하여 새로운 데이터 제약 스케일링 법칙을 제안한다.

2. Background

• 스케일링 법칙의 중요성: 언어 모델의 성능을 극대화하기 위해 필요한 컴퓨트 자원의 최적 분배를 에측하는 것은 LLMs 훈련에서 중요한 사항임. 이를 위해 사용되는 주요 metric은 모델이 보유한 데이터에 얼마나 잘 예측하는지를 측정하는 lossdlek.
  
• 손실을 최소화하기 위한 constraint을 효율적으로 할당하는 문제를 수식으로 정의한다. 이 과정에서, parameter와 training tokens 사이의 최적의 균형을 찾는 것이 중요하다.
• 기존 연구의 접근 방법
  - 고정 매개변수 (Fixed Parameters): 매개 변수의 크기를 고정하고 데이터의 양을 변화시켜 훈련하는 방식
  • 고정 FLOPs (Fixed FLOPs): 계산량을 고정하고 매개변수 크기와 훈련 토큰의 양을 변화시켜 훈련시키는 방법
  • 매개변수 적합 (Parametric Fit): 손실을 매개변수와 데이터의 함수로 모델링하고, 이를 데이터로부터 학습하여 최적의 자원 할당을 예측한다.
• 매개변수와 데이터의 관계: 손실 L은 매개변수 N와 훈련 토큰 D의 함수로 표현된다. 이 관계를 이해하는 것은 자원을 어떻게 분배할지 결정하는 데 중요하다. Chinchilla 연구에서는 매개변수와 데이터를 비례적으로 확장하는 것이 컴퓨트 최적화에 효과적이라는 결론을 내렸다.
• 컴퓨트 최적화 공식: L, N, D 간의 관계를 수학적으로 모델링하고, 주어진 컴퓨트 자원 C에 대해 최적의 매개변수 N과 데이터 D를 계산하는 공식을 제공한다. 이 공식은 연구자들이 이론적으로 자원을 최적으로 할당할 수 있도록 돕는다.
  

3. Method: Data-Constrained Scaling Laws

• 데이터 제약 조건 하에서 대규모 언어 모델을 스케일링할 때의 최적 자원 할당과 반환 값을 예측하기 위해 새로운 스케일링 법칙을 개발하고 적용하는 방법을 설명한다.
  

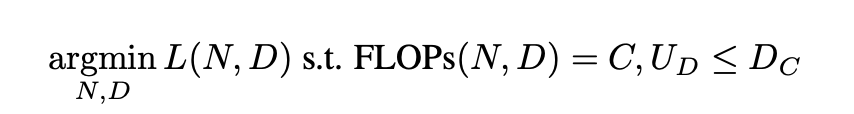
3.1. Parametric Fit

• 데이터 반복의 가치 평가: 데이터가 제한적일 때, 동일 데이터를 여러 epoch에 걸쳐 반복하여 사용하는 것의 효과를 평가한다. 이를 위해 반복 데이터의 효율성을 측정하는 새로운 스케일링 법칙을 도입한다.
  $R_D$가 커질수록, 반복되는 token이 0에 가까워지고 D'은 D보다 작아진다.
• 손실함수 수정: 기존의 손실 함수를 수정하여 반복되는 데이터와 매개변수의 효과적인 활용을 고려한다. 새로운 스케일링 법칙은 반복되는 데이터가 줄어드는 가치와 모델의 매개변수가 초과할 경우 발생하는 감소 효과를 모델링한다.
• 데이터 제약 DC를 고정하고, 매개변수와 epoch 수를 변화시켜가며 모델을 훈련시키는 실험을 설게한다. 이는 자원 할당의 최적화를 탐색한다.
• 고정된 FLOPs: 계산 리소스를 고정하고 다양한 데이터 제약 조건에서 모델을 훈련하여 반복 데이터의 반환 값을 분석한다.
• 매개변수 적합: 모든 훈련 실행에 대한 데이터를 사용하여 제안된 스케일링 법칙의 예측 능력을 평가한다.
• 효과적 데이터와 매개변수: 반복되는 데이터의 가치가 시간이 지남에 따라 감소하는 것을 모델링하기 위해, 새로운 스케일링 법칙은 효과적 데이터와 매개변수의 개념을 도입한다. 이는 반복 횟수에 따라 조정되면, 초기 유니크 데이터 사용에 최적화된 매개변수 수를 계산하는 데 사용된다,
• 반복의 경제학: 데이터를 반복하는 것이 가져오는 이득과 비용을 계량화하고, 이를 통해 데이터 제약이 있는 환경에서 모델 성능을 최대화하기 위한 가장 효과적인 훈련 전략을 제시한다.
  
  

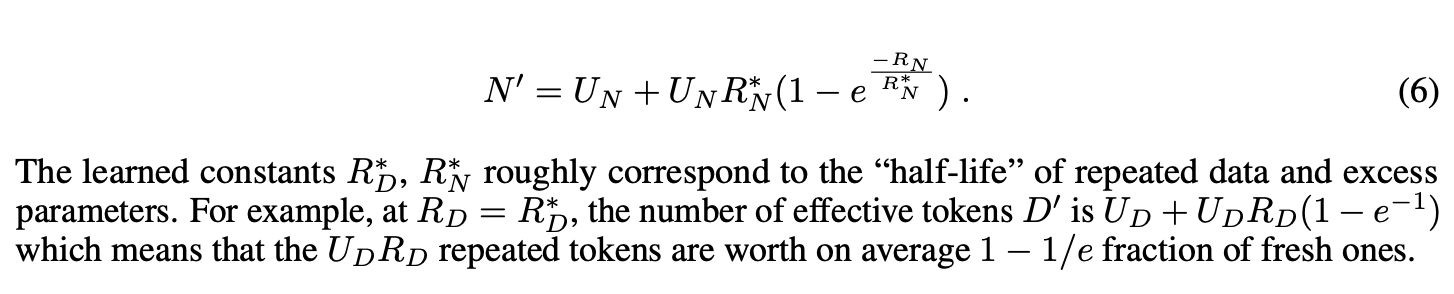
4. Experimental Setup

• GPT-2 architecture, tokenizer
• 8.7 billion parameters
• trained for up to 900 billion total tokens
  

5. Results: Resource Allocation for Data-Constrained Scaling

• 데이터 제약: 고정된 데이터 예산 (100M, 400M, 1.5B tokens), 이를 기반으로 다양한 parameter 크기와 epoch 수를 가지는 모델을 훈련
• epoch, parameter의 효과 분석
  
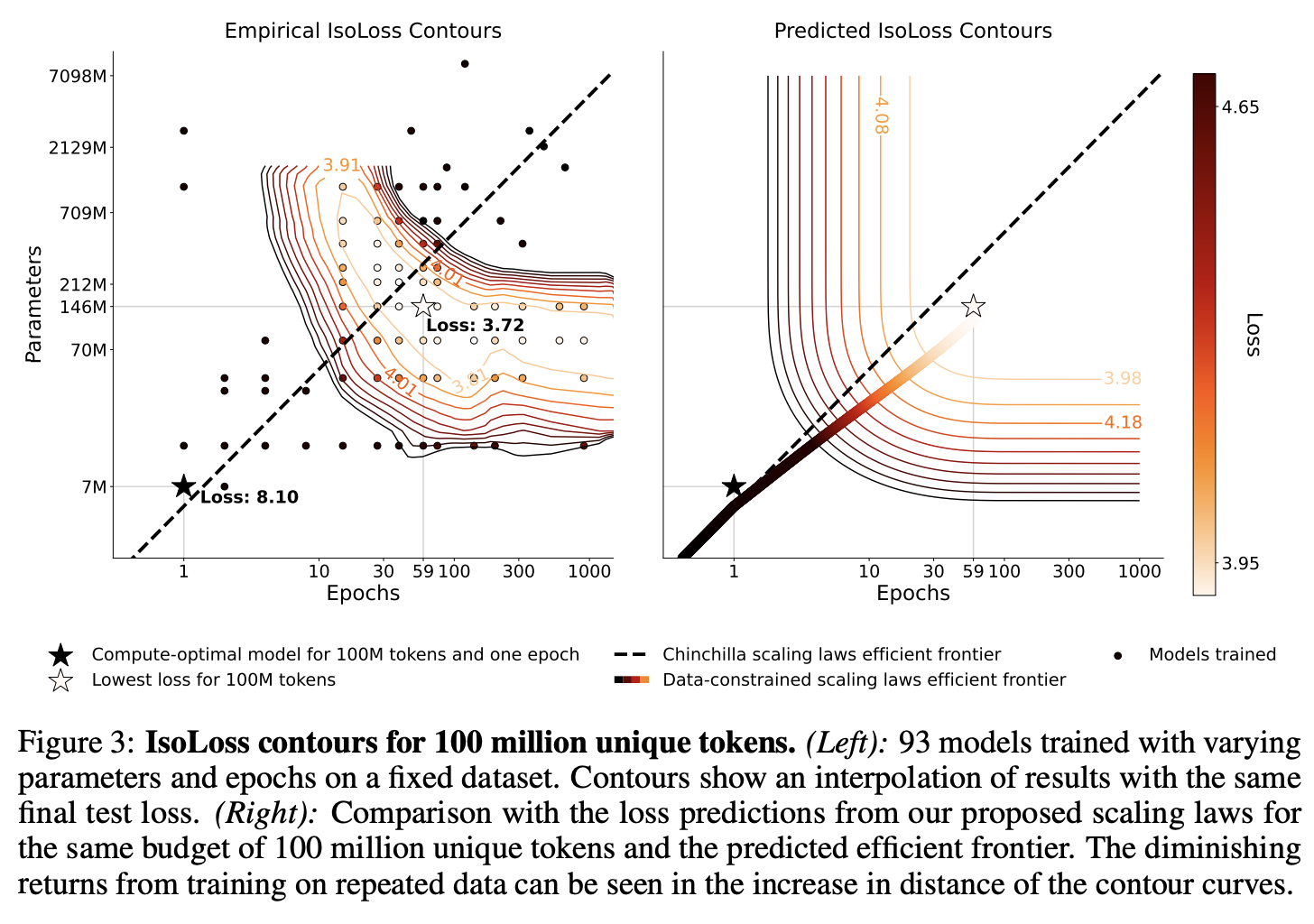
  단일 에포크에 비해 최대 4개 에포크까지는 유사한 검증 손실을 보이며, 이후로는 추가적인 에포크가 모델 성능에 미치는 긍정적인 영향이 감소한다.
• Different Data Constraints
  
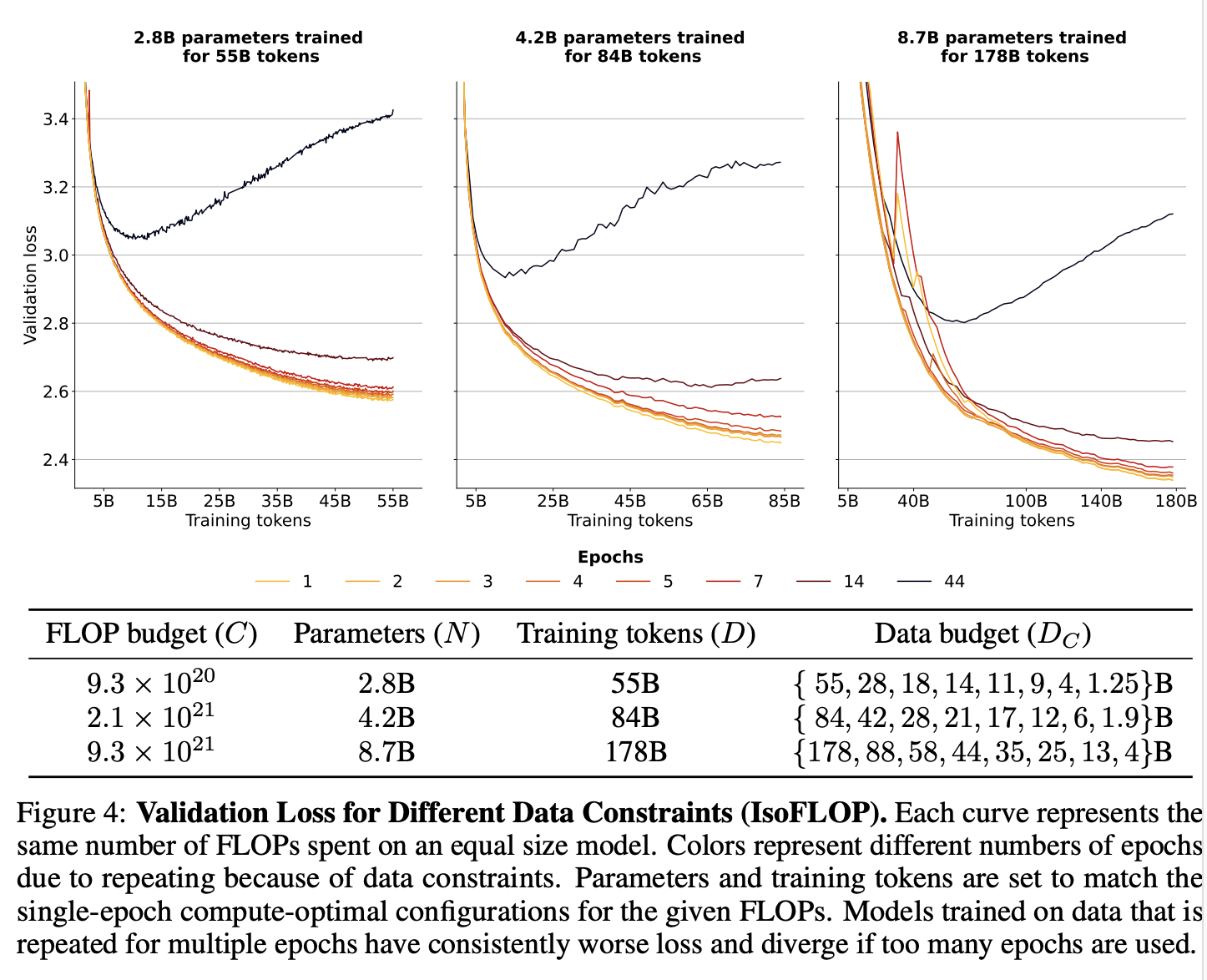
  데이터 제약 조건에서의 실험 결과는 epoch 수를 적당히 올리는 것이 매개변수 수를 무작정 늘리는 것보다 더 효과적일 수 있음.
  

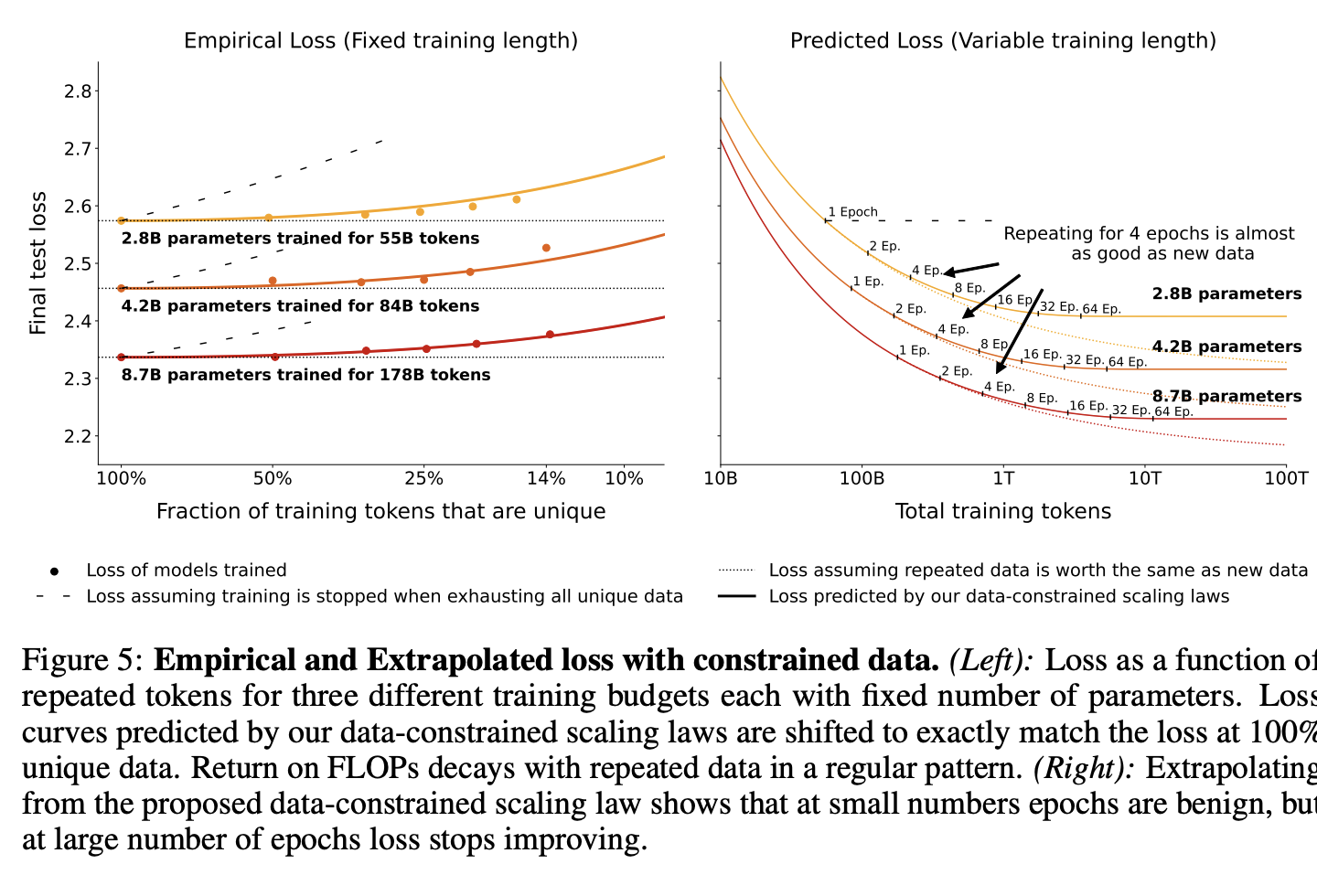
6. Results: Resource Return for Data-Constrained Scaling

• FLOP 예산, 데이터 예산을 설정하고, 이에 따른 모델 성능을 측정한다.
• 반복 데이터의 가치: 특정 epoch까지는 반복 데이터가 유사한 가치를 제공하지만, 그 이후에는 그 가치가 급격히 감소함을 관찰할 수 있다.
• 최적 데이터 사용: 제한된 데이터 예산 내에서 최적의 성능을 내기 위한 매개변수와 epoch의 조합을 식별한다. 이는 더 많은 에포크를 반복할 때의 이점과 한계를 구체적으로 보여준다.
• epoch 반복의 효과: 초기 몇 epoch 동안은 반복된 데이터가 상대적으로 높은 가치를 유지하지만, 일정 에포크를 넘어서면 반환값이 급격히 줄어든다. 이를 통해 데이터 반복의 경제적 효과를 정량적으로 분석한다.
• 이론적 손시로가의 비교: scaling 법칙에 기반한 에측 손실과 실제 훈련 데이터를 통한 손실을 비교함으로써, 제안된 스케일링 법칙의 정확성을 검증한다.

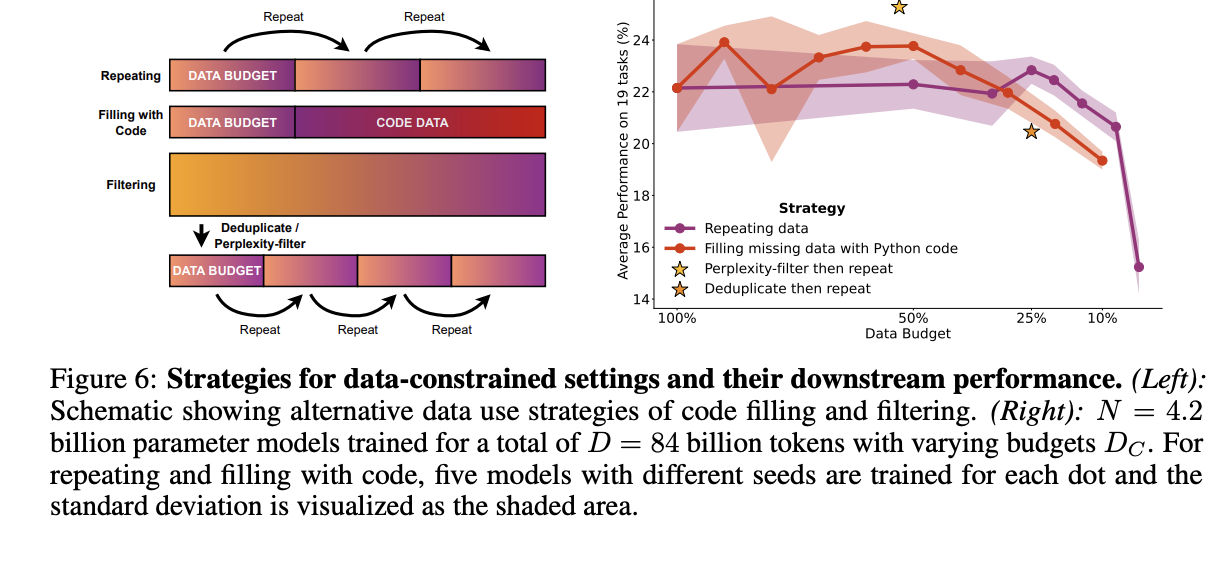
7. Results: Complementary Strategies for Obtaining Additional Data

• 코드 데이터 혼합 : 다양한 비율로 코드 데이터를 추가
• 필터링 전략 조정 : 기존 필터링 기법을 완화하거나 변경함으로써 훈련 데이터의 양을 증가시키고, 이를 통해 모델의 다운스트림 성능에 미치는 영향을 평가한다.
• 성능 향상: 코드 데이터를 추가한 모델은 기존 자연어 데이터만 사용한 모델보다 높은 성능을 보여주며, 이는 추가 데이터 모델의 다양한 능력을 향상시킬 수 있음을 시사한다.
• 필터링 기법의 영향: 중복 제거, 난이도 기반 필터링 조정 - 데이터 질적인 측면에서는 개선이 있었지만, 이러한 변화가 모델의 일반화 능력에 미치는 직접적인 영향은 제한적일 수 있다.
• 데이터 전략의 선택: 연구 결과는 데이터 제약 조건에서 언어 모델을 확장할 때 다양한 데이터 전략을 고려해야 함을 강조한다. 특히, 다양한 데이터 소스와 필터링 전략을 적절히 조합하여 사용하면, 데이터의 양과 질을 동시에 관리할 수 있다.

8. Related Work

Large Language models, Scaling Laws, Alternative data strategies

9. Conculsion

• 데이터 제약 조건에서의 스케일링 법칙과 그 효과에 대해 강조. 연구를 통해 개발된 새로운 스케일링 법칙이 기존의 이론을 어떻게 개선하고, 실제 언어 모델 훈련에 어떤 시사점을 주는지 정리
• 이론적 및 실용적 기여, 향후 연구 방향 등을 볼 수 있음