Geometric Order Learning for Rank Estimation

사람 얼굴을 보고 나이를 추정하는 task 나 사진에게 미적 점수를 메기는 task 와 같은 rank estimation task는, 일반적인 classification 문제와는 다르게, 점수의 order 를 고려해야 한다. 고로 embedding space 에 encoding 할 때 여러 시도가 있었는데 이번 논문에서는 metric loss, order loss 와 같은 geometric constraints 를 활용해 order 와 metric relation 을 표상하고자 하였다. 또한 rank estimation task의 성능을 평가하기 위해 discriminative ratio for ranking (DRR) 새로 고안하였다.

Introduction

rank estimation task 는 object 의 rank (or ordered class) 를 추정한다. 예를 들어 movie rating 을 할 때, class 는 outstanding, very good, satisfactory, unsatisfactory, and poor 로 나뉠 수 있다. 이 문제를 풀기 위해 order 정보를 이용하는 order learning 과 'distance'를 활용해 representation space 상에서의 push / pull 을 강제하는 metric learning 방식이 이용되어 왔지만, 이를 함께 사용한 연구는 없었다.

이번 연구에서 저자 연구진은

• embedding space 상에 표상된 object 의 direction 과 distance 를 함께 고려하여 그들의 order 와 metric relation 을 표상하는 모델 디자인을 제안하였고,
• 이를 평가하기 위한 DRR 이라는 새로운 metric 을 도입했으며,
• facial age estimation, HCI classification, aesthetic score regression problem 에서 state-of-the-art 성능을 기록하였다.

Related Work

관련 기존 연구들을 ordinal regression, order learning, metric learning 세 필드로 나누어 자세히 소개하고 있다. (소개된 몇몇 논문들을 살펴보았을 때 굉장히 흥미로운 접근이 많았다.) 자세한 내용은 논문에서 참고하면 좋을 것 같다.

Proposed Algorithm

Preliminary - Order and Metric

수학적으로 order 과 metric 은 "binary relation" 이다. (이산구조)

예를 들어, $\theta_i$ 가 i-years-olds 를 의미한다고 했을 때, $\theta_{17} < \theta_{32}$ 는 17살이 32살 보다 어리다 를 의미한다.
(중요)

• Let $\theta(\cdot)$ be the rank function, and let x and y be instances.
• Then, $\theta(x) = \theta_{17}$ means person x is 17-year-old.
• Also metric describes the difference between ranks in $\Theta$. $d(\theta(x), \theta(y))=15$ means two people x, y are 15살 차이.

Embedding Space Construction

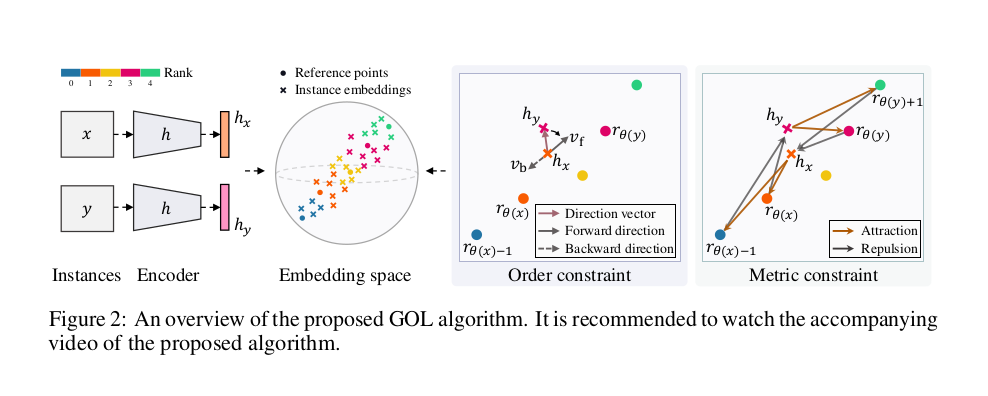
Geometric Order Leraning (GOL) 은 directional (order), distance (metric) relationships between object instances 를 강제하는 geometric constraints 를 활용한 geometric approach 이다. 구체적으로, rank 에 따라 instance 를 "sort" 하고, two instance 의 rank difference 에 따라 metric constraint 에 의한 separation 정도를 달리한다.

Order Constraint
training set $\Chi$ 에 $M$ ranks 가 존재한다고 가정했을 때, ranks 는 $\Theta = \{0,1,...,M-1\}$ 로 쓸 수 있다. 위 그림에서 encoder h 는 instance $x \in \Chi$ 를 feature vector $h_x=h(x)$로 mapping 시킨다. h 는 fully connected lyaer 를 제외한 VGG16 을 사용했고, output vector 는 pooling layer 를 거쳐 nomarlization 되었다. (그러므로 embedding space 는 unit hypersphere)

이 때, instance x 와 y 사이의 "ordering"을 다음과 같이 세 개의 카테고리로 나눌 수 있다

이런 식으로 세팅하면, 만약 x<y 일 때 $h_x$ 와 $h_y$ 가 그들의 rank 대로 잘 align 이 되어야 한다. 이러한 rank direction 을 modeling 하기 위해 M 개의 "LEARNABLE" parameter 인 reference point $r_0,r_1, ..., r_{M-1}$ 를 도입하였다. reference point 는 embedding space 내에서 M ranks 의 positions 을 guide 해주고, randomly initialized 되며 encoder parameter 와 함께 jointly optimized 된다.

이러면 v(ri, rj) 는 i rank에서 j rank의 rank direction 을 의미하게 된다. 만약 i<j 면 forward, i>j 면 backward 가 될 것 이다. 이를 이용해 $v_f$ 와 $v_b$ 를 정의한다.

그리고 정의된 forward and backward rank direction 을 이용한 constraint 를 유도한다. 이를 soft 하게 활용하기 위해 exponential sum 형태로 만들어주고, symmetric cross entropy loss 로써 order loss 를 정의해주었다.

Metric Constraint
metric constraint 는 embedding space 내에서 instance feature vector 간의 distance 가 rank difference 를 반영하는 것을 목표로 만들어졌다. 다음과 같은 관계를 목표로 한다.

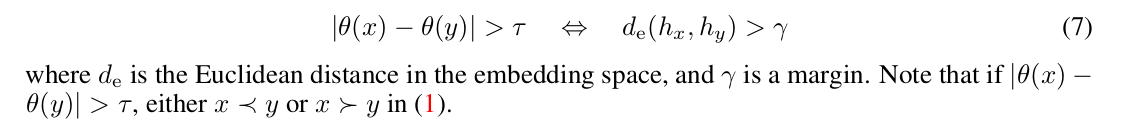
또한, 다를 때 이외에도 비슷할 때는 다음과 같이 표현할 수 있다.

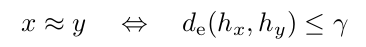
Triangle inequality 에 의해, (7)번 식과 그 아래 식을 reference point ri 를 거친 방정식으로 세워 다시 표현할 수 있다.

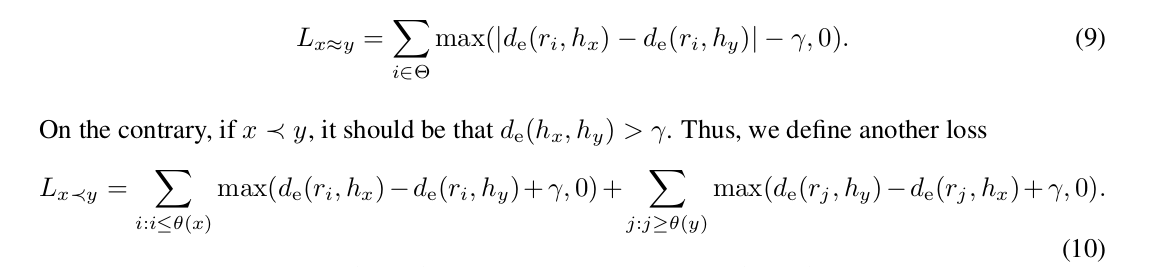
9번 식을 보면, x~=y 일 때 d와 d 차이가 loss term 에 포함되어 있고 차이가 줄어들기를 원하는 식으로 해석할 수 있다. 비슷하게 10번 식을 보면, rank 가 작은 instance 에 대해서, 작은 instance 의 rank 보다 작은 rank reference point 들에 대해, 서로 거리가 커졌으면 좋겠고, 마찬가지로 rank 가 큰 instance 에 대해서는 큰 instance의 rank 보다 큰 rank reference point 들에 대해, 서로 거리가 켜졌으면 좋겠다는 설계의도를 가지고 있다.

또한 주목해볼 만한 점은, 두 instance 의 rank 사이의 rank reference point $r_l$ ($\theta(x) < l < \theta(y)$) 는 제외되었다는 점이다. 가운데에 있기 때문에 guidance 할 때 별로 도움이 되지 않을 것이라는 생각이 들어있다.

마지막으로 reference point $r_i$ 를 통해 indirectly attract or repel 하도록 설계되었는데, 이는 direct 하게 적용했을 때 arbitrary direction 으로 이동할 수 있기에 방향을 guide 하기 위해 이러한 reference point 를 쓴 것이라고 언급하고 있다.

이러한 loss 를 멀끔하게 쓰면 다음과 같이 쓸 수 있다.

이 때 $[\cdot]$ 는 indicator function 이다.

Loss Function
order and metric constraint 이외에도 reference point 주변으로 모이도록 하는 center loss (기존 연구) 를 추가해 주었다.

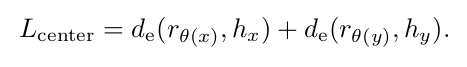
forward and backward rank direction 정보를 활용한 order loss 를 통해 instance 가 그들의 rank 에 따라 embedding space 상에서 sort 되도록 하였고, center loss 를 통해 reference point 를 중심으로 잘 cluster 되도록 하였으며, 마지막으로 rank difference 에 따라 repulsion 과 attraction guide 를 수행하는 metric loss 로 좋은 embedding space 를 construct 하고자 하였다.

k-NN Rank Estimation

실제로 instance 가 들어왔을 때 어떻게 rank 를 추정할 것인가는 다음과 같이 k NNs 로 이루어진 set $\mathcal{N}$ 의 rank estimation function 값의 평균으로 구해준다.

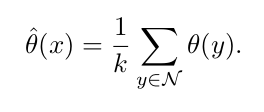
Experimental Results

Implementation

VGG16 pretrained 모델을 encoder h 로 사용했고, reference point 는 Glorot normal method 로 initialize 하였다. Adam optimizer, cosine annealing cycle scheduled learning, random horizontal flip only data augmentation 을 사용하였다.

Embedding Spaces

제안된 GOL algorithm 을 이용해 생성된 embedding space 의 quality 를 측정하기 위해 between-class variance to within-class variance (B2W) criterion 을 사용하였다.

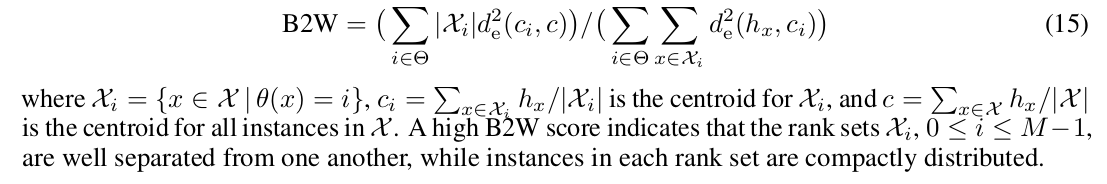
간단히 이해한대로 설명하면, 분자에 rank 간 구분이 없는 채로 instance 간의 거리를, 분모에는 rank 내에서 instance 간의 거리를 넣어준 식이다. 즉 B2W 가 높으면 높을수록 목표를 잘 이뤘다라고 해석할 수 있다.

하지만 B2W 는 ordinal relationship of ranks 를 잘 반영하지 못한다고 설명하며 이를 반영하는 새로운 metric인 discriminative ratio for ranking (DRR) 을 새로 제안하였다.

이는 the average pairwise centroid distance 와 the average pairwise instance distance in each rank set 간의 ratio 를 나타낸다. $\beta$는 rank difference 에 따라 해당 pair 의 weight 를 얼마나 emphasize 할지를 정하는 nonnegative parameter이다. (내가 이해하기론) 기본적인 theme 자체는 B2W 와 유사하게, 분자에 서로 다른 rank 의 centroid 의 거리를, 분모에는 같은 rank 내 instance 들의 거리를 했다는 점에서 B2W와 유사한 성격을 띄지만, pair 를 설정하여 이 둘의 rank difference 를 반영하는 목적이 식에 잘 녹아있다는 생각이 든다.

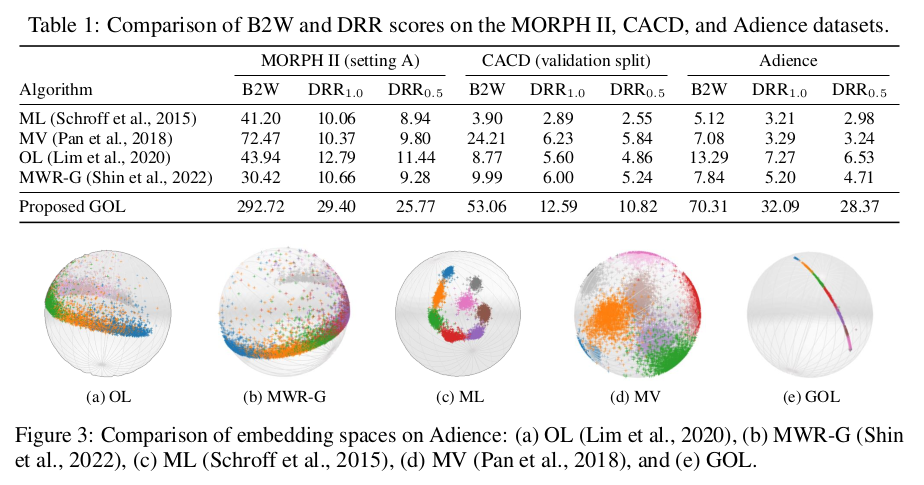
Table 1 에서 3가지 데이터셋에 대해 모든 metric 에서 기존 방식들보다 높은 성능을 보여주었다. 다른 방식을 쓸 때 encoder backbone 은 모두 동일하게 사용했다. 또한 DPR1.0 성능 향상이 DPR0.5 성능 향상보다 컸고 이는 rank set 을 잘 arrange 했다고 해석할 수 있다.

Figure 3 은 Adience dataset 을 visualize 한 결과이다. 다른 모델에 비해 아주 나이스하게 그려진 것을 확인할 수 있다. a,b 는 sort 되었지만 scatter 되어있고, c는 well cluster 되었지만 metric relation of rank 가 반영되어 있지 않으며 d 방식은 둘 다 이루어지지 않았다. 반면 e 에서는 두 정보가 모두 반영되어 있는 것을 확인할 수 있다.

(어떻게 했는지는 정확히 이해하지는 못했다. 쓰여있기로는 fully connected layer with 3 output neurons to each encoder for the visuazliation 이라고 쓰여있다. supplementary appendix 를 봤을 때, VGG16 228x228x3 을 사용한 것이 아니라 ResNet18 에 28x28x3 을 사용했고 output dimension 이 3이 되도록 사용했다고 쓰여있다. 이해하신 분 계시면 댓글로..) -> 아하 아마 autoencoder 를 이용했을 것 같다.

Rank Estimation

Embedding space 가 잘 construct 되었기 때문에 단순한 kNN rule 만으로 우수한 rank estimation 결과를 얻었다고 설명하고 있다.

Facial age estimation

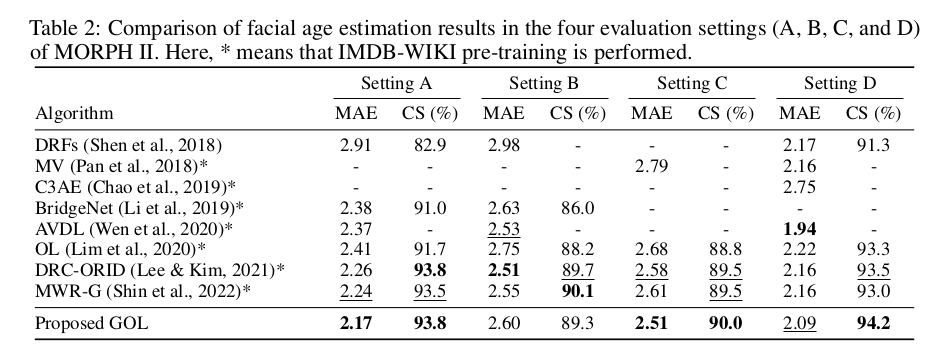
mean absolute error (MAE) 는 ground truth age 와 예측한 age 와의 error 를 계산한 것이고, cumulative score (CS) metric 은 absolute error 가 특정 tolerance level 을 넘지 않는 percentage 를 계산한 것이다. MORPH II 의 four evaluation setting (A,B,C,D) 중 가장 어려운 task 인 C 를 포함한 5개의 task 에서 best performance 를 보였다.

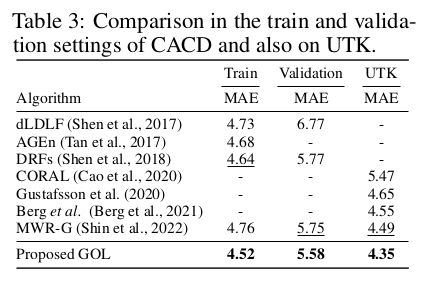
또한 Table 3 에서 best performance 임을 보여주고 있다.

HCI Classification and Aesthetic score regression

다른 task 에서도 우수한 성능을 보여주었다. (자세한 내용은 논문 참조)

Analysis

Ablation study

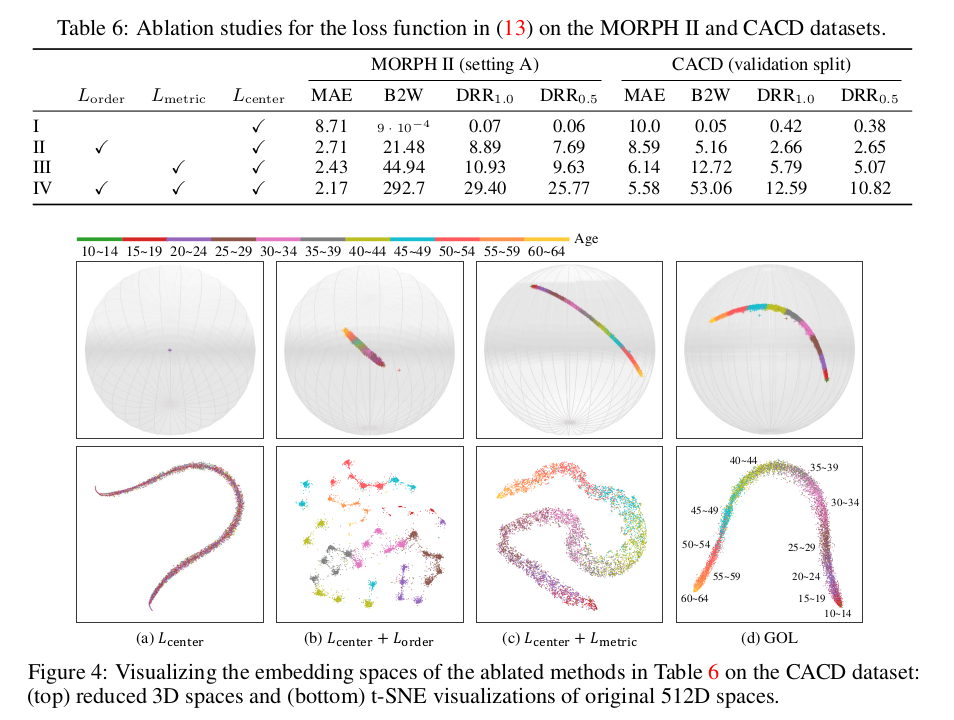
Table 6 와 Figure 4 에서 Loss term 과 관련한 ablation study 결과를 확인할 수 있다. order and metric constraint 가 성능 향상에 도움이 되고 상호 보완적인 관계를 보임을 확인할 수 있다.

Alternatives to $L_{x<y}$

III 이 GOL 에서 사용한 식이다. I 은 reference point 를 사용하지 않고, II 는 pair 마다 딱 두 개의 reference point 를 사용한다. III 을 사용했을 때 MAE 가 낮음을 확인하였다.

Embedding space transition

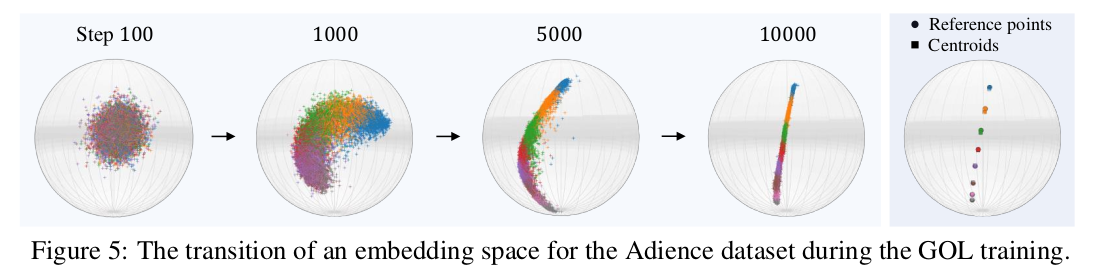
training step 에 따라 gradually sorted and separated 되는 것을 확인할 수 있다.

Comparison with order learning

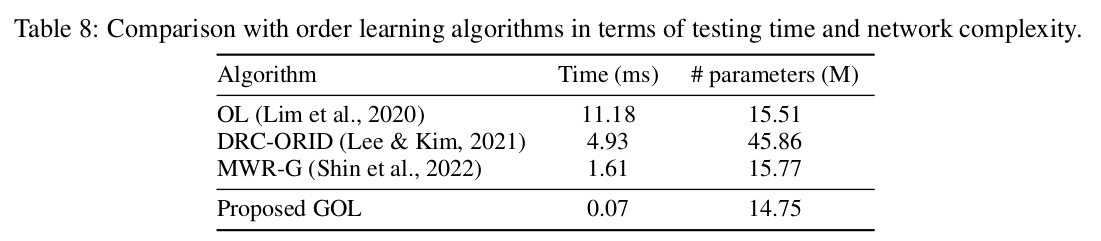
time complexity 와 network complexity 면에서 모두 efficient 하다는 것을 확인할 수 있다.

Conclusion

order and metric relation 을 반영하는 geometric constraint 를 활용한 embedding space 를 구성하였다. 이후 simple kNN rule 로 rank estimate 를 하였고, 추가적인 실험에서 GOL이 high-quality embedding space 를 구성했고 excellent rank estimation result 를 기록했음을 확인하였다.

적용할 분야가 무궁무진한 연구라고 생각한다. 개인적으로 embedding space representation 에 관심을 가지고 self-supervised learning 등에 관심을 가지기 시작했었는데 이러한 흥미롭고 잘 설계된 연구를 봐서 기분이 좋다. 얼른 적용해보고 싶다.