
Intro
지난 포스트인 Sequence-to-Sequence with Attention에서 sequence-to-sequence 모델의 경우 RNN 계열의 순환 신경망을 사용함으로 인해 입력 시퀀스가 길어질 수 록 하나의 Context Vector에 모든 정보를 담기 부족하다는 한계가 있음을 확인하였다. 그로 인해 Attention mechanism이 적용되었지만 이 또한 결국 문장에 가중치만 줄 뿐 하나의 Context Vector에 문맥 정보를 압축한다는 점에서 같은 문제가 있었고, 이러한 시퀀스 순서를 유지하며 학습하는 RNN의 한계가 지적되었다.
이후 이러한 문제를 해결하기 위해 RNN셀이 전부 제거되고 Attention기법을 중점으로 학습하는 모델이 등장하였으니 그것이 바로 트랜스포머(Transformer) 모델이다.

Transformer
트랜스포머(Transformer)모델은 2017년 구글에 의해 소개된 논문인 "Attention is all you need"에서 등장한 모델이다. 기본적으로 트랜스포머 모델은 앞서 살펴보았던 Sequence-to-Sequence의 인코더(Encoder), 디코더(Decoder)의 구조를 가지고 있지만 RNN셀을 사용하지 않고 단순히 어텐션(Attention)구조만으로 이루어져 있다는 것, 그리고 이러한 인코더-디코더 구조가 n개(논문에서는 6개) 존재한다는 것이 큰 특징이다.
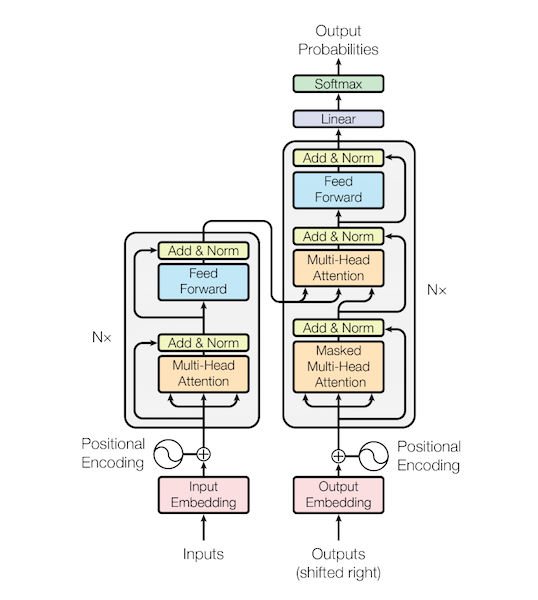
위 그림은 트랜스포머 모델의 전체적인 아키텍처이다. 크게 왼쪽 부분을 인코더(Encoder)로 구분하고, 오른쪽을 디코더(Decoder)로 구분하며 이러한 구조가 n개 존재한다. 학습 방법은 seq2seq모델과 같이 인코더에서 입력 시퀀스의 특징을 학습하고 이를 디코더의 입력 벡터로 넘겨주어 하나의 토큰씩 출력하게 된다. 하지만 seq2seq와 크게 다른 점은 시퀀스 순서를 학습하기 위한 RNN셀을 사용하지 않는다는 것인데 그것을 대체하기 위해 Positinal Encoding이라는 기법을 사용하였으며, 기존 Attention과 비슷하면서도 조금 다른 Self-Attention과 Multi-Head Attention이라는 기법을 적용하였다. 아래에서 각 부분에 대해 자세히 살펴보도록 하자.
Positional Encoding
위에서 언급했다시피 RNN셀을 통해 순차적으로 시퀀스를 입력받는 seq2seq와 달리 트랜스포머 모델은 입력 시퀀스가 순차적으로 입력되는 것이 아니라 한번에 병렬적으로 인코더로 입력된다. 이렇게 모든 단어가 한번에 입력되면 입력 단어들의 순서정보를 보존할 수 없게 되는데, 이런 문제를 해결하기 위한 방법이 바로 Positional Encoding이다.
순서정보를 유지하기 위한 Positional Encoding함수의 수식은 아래와 같다.
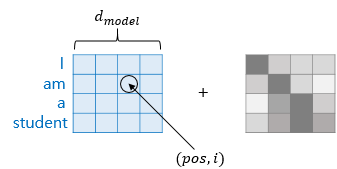
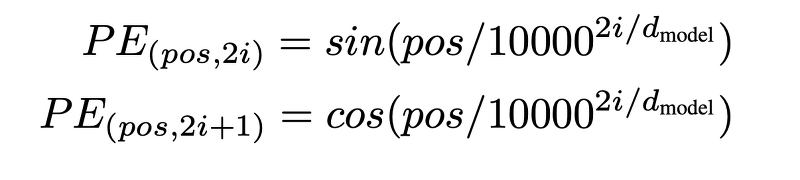
위 수식의 'pos'는 임베딩 벡터의 위치를 나타내고 'i'는 인덱스를 나타낸다.
위 수식을 살펴보면 인덱스가 짝수(pos, 2i)인 경우는 사인(sin)함수를 적용하고, 홀수(pos, 2i+1)인 경우는 코사인(cos)함수를 적용하여 순서 정보를 반영해주는 것을 알 수 있다.
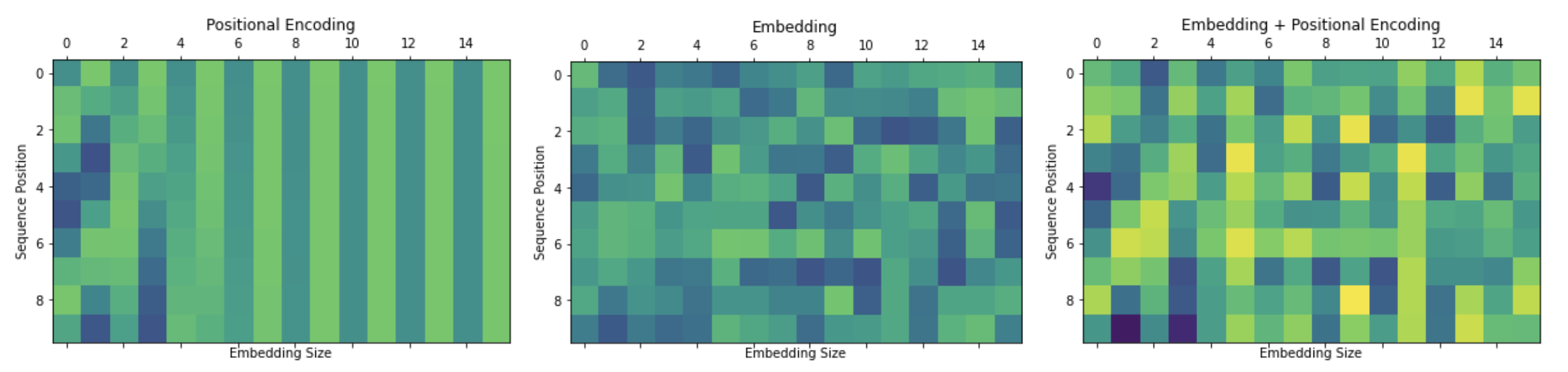
이렇게 계산된 포지션 임베딩 행렬(Positional Embedding Matrix)은 입력 원본 문장의 임베딩 행렬(Input Embedding Matrix)에 단순 덧셈연산을 통해 더해져 인코더의 input으로 사용되게 된다.
Self-Attention
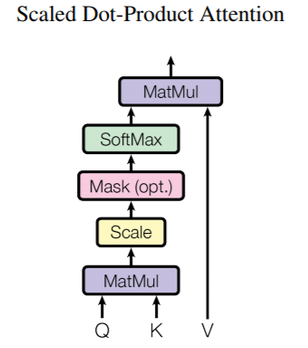
Self-Attention은 기존 Attention개념과 크게 다르지 않다. 기존 Attention은 디코더에서 예측하고자 하는 시퀀스(Query)를 인코더의 모든 시퀀스(Keys)와 내적연산을 통해 계산하였었는데,
(참고 : Seq2Seq with Attention 모델에서의 Attention)
Self-Attention은 말 그대로 Attention 연산을 해당 문장 시퀀스 자체에서 수행하는 것을 말하며 다른 점은 기존에는 내적(Dot-Product) 연산을 수행하였는데 트랜스포머 모델에서는 스케일 내적(scaled Dot-Product) 연산을 통해 Attention을 수행한다는 것이다.
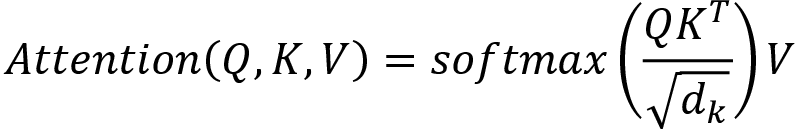
위 수식을 보면 key를 전치 후 query와 내적 연산을 한 후, Dk(key의 차원(dimension))를 제곱근한 값으로로 나눠주는 것을 알 수 있다. Scaling을 해주는 이유는 query와 key의 차원이 클 수 록 내적 연산을 통한 값도 계속해서 폭증하게 되는데 이렇게 되면 후에 Softmax함수에서 학습이 잘 안되기 때문에 이러한 경우를 위해 차원의 루트값으로 나눠주는 것이다.
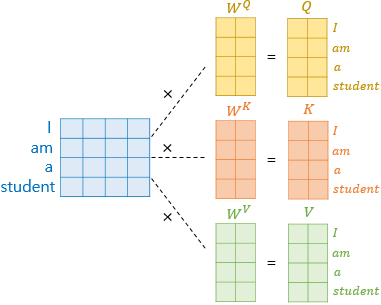
그리고 주의할 점은 self-attention 연산이 각각의 벡터마다 한번씩 이루어지는 게 아니라 행렬(maxtrix) 연산으로 이루어진다는 것이다. 이것을 외적(Outer-Product) 연산이라고 하는데, 각각의 벡터에 내적 연산을 하나 벡터 매트릭스 자체에 외적 연산을 하나 결국 동일한 연산이고, 한번에 외적 연산을 수행하는 것이 더 컴퓨팅 연산 상 효율적이다.
Multi-Head Attention
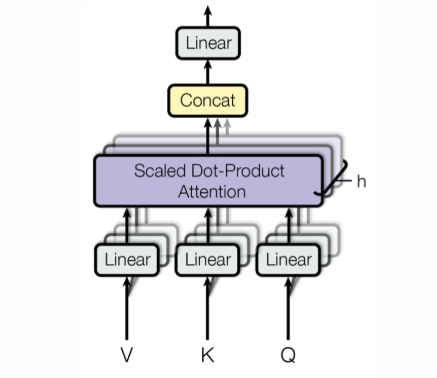
그리고 위에서 살펴 본 self-attention을 한번만 수행하는 것이 아니라 Query, Key, Value의 특징값을 헤드 수만큼 나눠서 여러번 Self-Attention을 수행한 후 각각의 값을 합산하는 것을 Multi-Head Attention이라고 한다.
아래는 Multi-Head Self-Attention의 전체적인 프로세스이다.
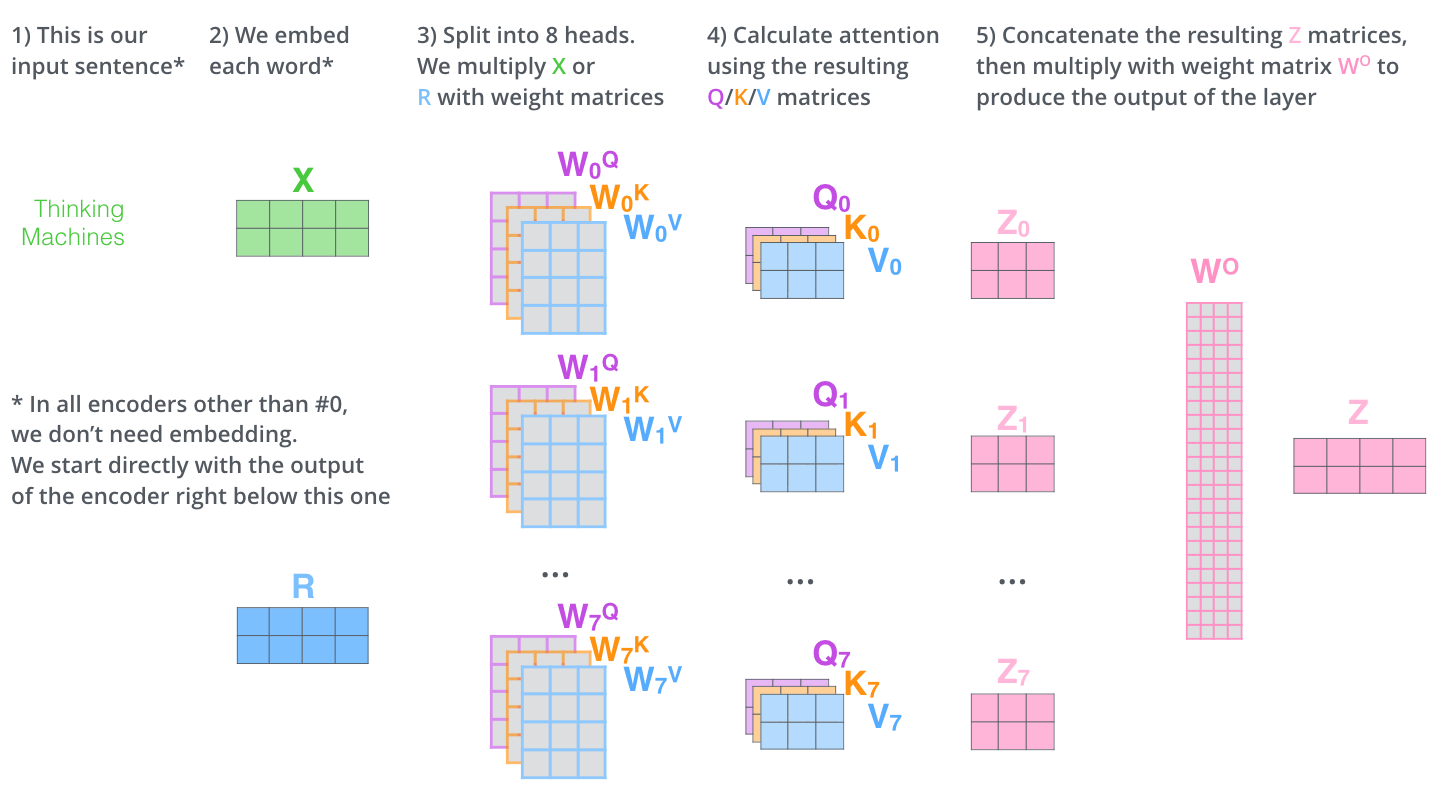
Masked Multi-Head Attention
Masked Multi-Head Attention은 디코더 단에서 수행되는 것으로 Multi-Head Attention과 근본적으로 동일하나 다른 점은 Self-Attention 계산 수행 시 현재 시점보다 앞에 있는 시퀀스들과만 Attention을 수행하고 뒤에 오는 시퀀스는 참조하지 않는 것을 말한다.
기존 seq2seq와 같은 순환 신경망 모델은 시퀀스가 순차적으로 입력되기 때문에 앞쪽부터 순차적으로 업데이트 되어온 hidden state을 다음 시퀀스 예측을 위해 사용하게된다. 하지만 언급했다시피 트랜스포머 모델은 입력 시퀀스가 한번에 들어가기 때문에 현재 시점보다 뒤에 올 시퀀스의 정보까지 알 수 있게 된다. 현재 시점의 값도 알지못하는데 뒤에 올 정보를 참조한다는 것은 직관적으로도 틀리다. 그래서 현재 시점보다 뒤에 있는 시퀀스를 참조하지 않기 위해 Masking을 한 후 Self-Attention을 수행하게 된다.
Residual Connection & Layer Nomalization
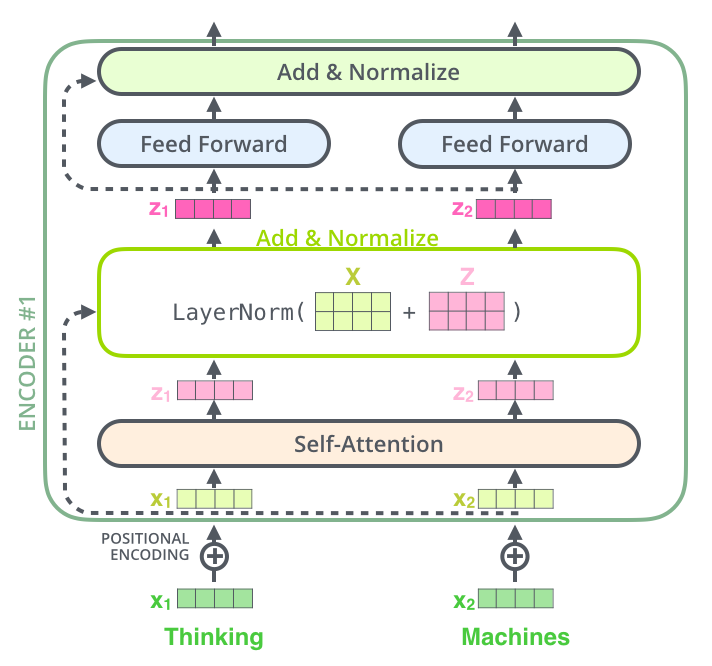
위 그림을 보면 점선으로 표시된 화살표가 Attention 레이어와 Feed-Forward 레이어를 지나쳐 Add & Normalize 해주는 부분이 있는데, 이 부분에서 Residual Conntection과 Layer Normalization이 수행된다.
Residual Connection이란 ResNet(Residual Network)에서 나온 개념으로 보존된 identity를 현재 레이어를 뛰어넘어 다음 레이어로 더해주는 방법을 말한다. 당시 ResNet은 2015년 ImageNet대회에서 높은 성능을 보였는데 이러한 학습 방법이 앙상블(Ensemble) 학습과 같은 효과가 있고, 경사소실(Gradient Vanishing) 문제에 도움이 되어 더 깊은 신경망 학습이 가능하다고 한다.
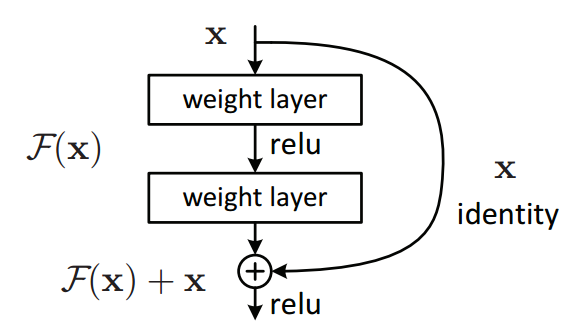
우선 Residual Connection은 학습시 입력값을 보존하였다가(identity x) 비선형 활성화함수(ReLU)를 거친 다음 레이어의 값에 직접적으로 더해줌으로써 gradient가 소실되는 것을 방지하고, 이후 수행될 Layer Normalization의 학습 효율을 증대시킨다.
트랜스포머에서는 인코더와 디코더 모두에서 사용되며 각각 Attention Layer와 Feed-Forward Network를 거치기 전 입력값에 대해 Residual Connection과 Layer Nomalization을 수행한다.
Conclusion
처음 트랜스포머 아키텍처를 봤을 때 인코더와 디코더 내에서 각각 여러 개의 레이어를 거치는 모습을 보고 복잡한 구조라고 생각했었다. 그런데 막상 보니 기존 Sequence-to-Sequence with Attention 원리 자체는 크게 다르지 않은 것 같고, 모델 사이즈의 증가와 약간의 학습방법의 차이만 존재하는 것 같다.
최근 대다수의 pretrain 모델이 트랜스포머 아키텍처를 base로 설계되고 있기 때문에 굉장히 중요한 모델임에 틀림없는 것 같고, 이후 등장한 BERT, XLnet RoBERTa, BART 등과 같은 모델들도 단지 training 방법에 차이만 있을 뿐이라 트랜스포머 아키텍처만 잘 알아도 쉽게 접근할 수 있을 것 같다.
트랜스포머 모델 또한 Tensorflow와 Pytorch 공식 문서에 tutorial이 준비되어 있느니 참고!
- Transformer model for language understanding
- SEQUENCE-TO-SEQUENCE MODELING WITH NN.TRANSFORMER AND TORCHTEXT
.jpeg)