BOJ 1904 01타일
문제 : 01타일

✅ 생각
n을 하나씩 증가시키며 만들 수 있는 2진 수열의 갯수를 확인해보자
| n(2진수열의 길이) | 만들 수 있는 2진 수열의 갯수 |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 5 |
| 5 | 8 |
| 6 | 13 |
| ... | ... |
증가하는 모습이 마치 피보나치 수열 "같다"
📍 피보나치 수열 맞나?
확인이 필요하다.
| n(2진수열의 길이) | 만들 수 있는 2진 수열 |
|---|---|
| 1 | |
| 2 | , |
| 3 | , , |
| 4 | , , , , |
n > 2일 때,
앞선 순서(n-2, n-1)에서 만들어준 타일을 이용해서
현재(n)의 타일을 만들어 준다고 생각해보자.
길이가 3인 2진 수열을 만들어주기 위해서
길이가 1인 2진 수열에는 00 을 붙여서 만들어 줄 수 있고,
길이가 2인 2진 수열에는 1 을 붙여서 만들어 줄 수 있다.
00 또는 1을 각 수열 뒤에 붙여준다고 생각하면,
중복되는 수열 없이 n-1, n-2 번째 수열로
n번째 수열을 만들어 줄 수 있다.
📍 2칸으로 피보나치 만들기
처음에 시간초과, 메모리초과가 나는 이유가
n의 범위() 때문인줄 알고
길이가 2인 리스트로 n번째 피보나치 수를 만들었다.
문제의 조건대로,
n=1, n=2일때 값은 1, 2이다.
두 숫자의 합을
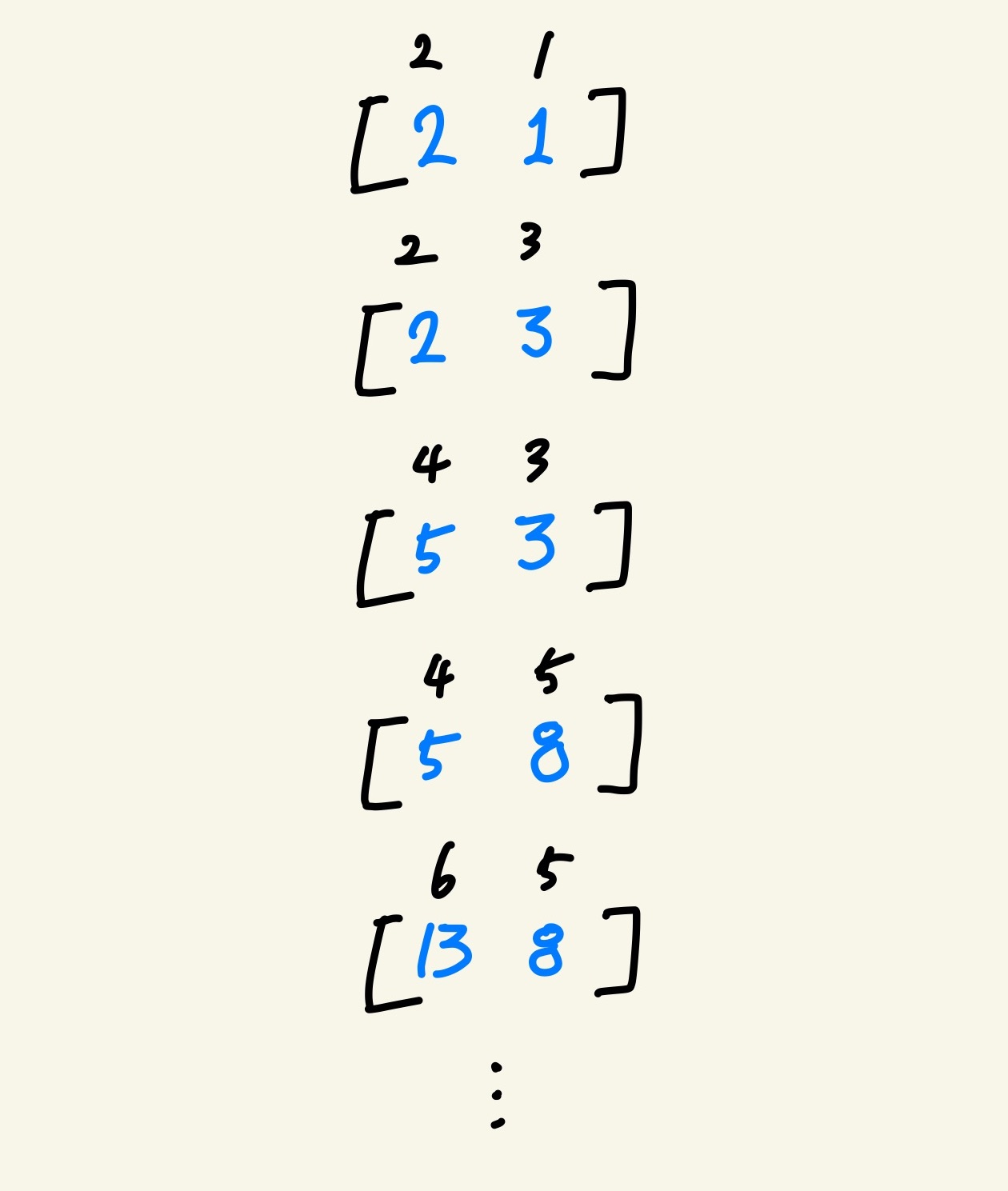
n이 홀수면 1번, 짝수면 0번 Index에 각각 갱신시키며,
n번째 피보나치 수를 n%2 index에 만들어 준다.
📍 나머지 정리
일 때
이다.
피보나치 수열은 이니까
각 항을 계산할 때 이를 적용해서 넣어준다.
메모리 초과와 시간 초과가 난 이유는 여기에 있었다.
파이썬은 큰 수를 List를 이용해서 처리하기 때문에
값이 메모리 범위를 벗어날 경우 계산 속도가 현저히 감소한다.
[전체 코드]
import sys
T = 15746
N = int(sys.stdin.readline().rstrip())
fibo_num = [2, 1]
def fibonacci(x):
for i in range(3, x+1):
fibo_num[i%2] = (fibo_num[0]%T + fibo_num[1]%T)%T
return fibo_num[x%2]
print(fibonacci(N))
