문제
문제
N개의 수로 이루어진 수열 A[1], A[2], …, A[N]이 있다. 이 수열에 대해서 버블 소트를 수행할 때, Swap이 총 몇 번 발생하는지 알아내는 프로그램을 작성하시오.
버블 소트는 서로 인접해 있는 두 수를 바꿔가며 정렬하는 방법이다. 예를 들어 수열이 3 2 1 이었다고 하자. 이 경우에는 인접해 있는 3, 2가 바뀌어야 하므로 2 3 1 이 된다. 다음으로는 3, 1이 바뀌어야 하므로 2 1 3 이 된다. 다음에는 2, 1이 바뀌어야 하므로 1 2 3 이 된다. 그러면 더 이상 바꿔야 할 경우가 없으므로 정렬이 완료된다.
입력
첫째 줄에 N(1 ≤ N ≤ 500,000)이 주어진다. 다음 줄에는 N개의 정수로 A[1], A[2], …, A[N]이 주어진다. 각각의 A[i]는 0 ≤ |A[i]| ≤ 1,000,000,000의 범위에 들어있다.
출력
첫째 줄에 Swap 횟수를 출력한다
예제
예제 입력
3
3 2 1
예제 출력
3
접근
버블 소트를 구현해볼까
버블 정렬은 '인접한 두 수의 대소관계가 정렬 기준과 다르다면 swap'하는 연산을하며 배열을 순회하고, 또 이를 전체 원소의 수 만큼 반복하는 정렬 알고리즘으로 의 시간복잡도를 갖는다.
버블 정렬을 구현하여 swap 회수를 체크한다면 시간 초과로 해당 문제를 통과할 수 없다.
swap이 일어나는 횟수를 알기 위해서는
[4, 1, 5, 3, 2] 라는 수열이 주어질 때,
어떤 식으로 swap이 발생하는지 확인해보자

위 그림과 같이 오름차순으로 정렬된 상태가 되기 위해서는 총 6번의 swap이 일어나게 된다.
이를 정렬된 상태와 비교해서 미리 알 수는 없을까?
배열의 각 원소들은 정렬된 상태가 되기 위해서 얼마나 이동해야 할까?
모든 원소들은 정렬된 상태의 자신의 위치로 이동하기위해 swap하기 때문에,
현재 위치와 정렬된 위치의 차이가 곧 swap횟수이다.
다만, swap을 할 때에는 2개의 수가 위치를 바꾸기 때문에,
정렬된 상태로 이동하는 수를 큰 수를 오른쪽으로 이동 할지, 작은 수를 왼쪽으로 이동 할지 조건을 정해주어야 했고,
나는 큰 수를 기준으로 배열의 뒤쪽(오른쪽)으로 이동시키며
원래 배열의 위치에서 정렬된 상태가 되기 위해 몇칸의 이동이 필요한지를 확인해보았다.
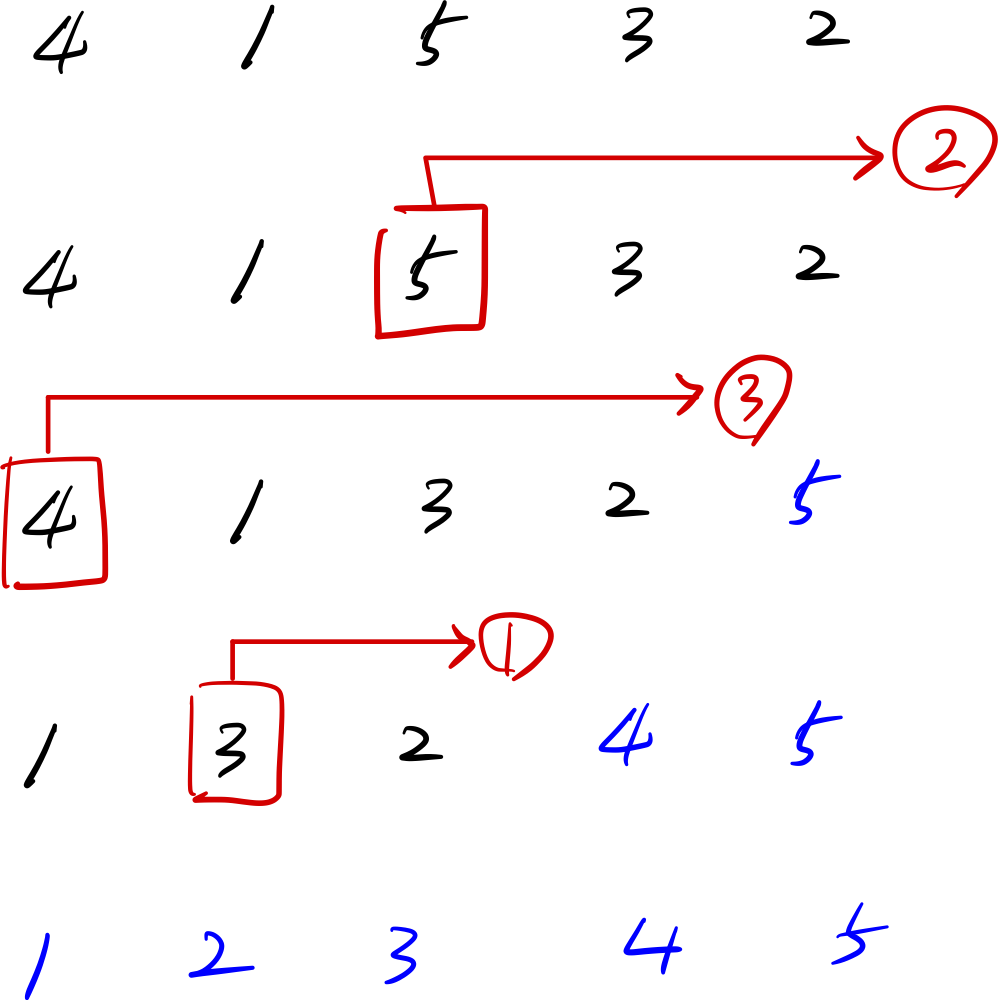
5는 정렬된 상태를 위해서 왼쪽으로 2번 이동해야하고,
4는 3번, 3은 1번 각각 순서대로 이동하면 배열이 정렬된 상태가 된다.
또, 당연하게도 이들의 합은 6으로 버블 정렬시 swap이 발생하는 횟수와 동일하다.
다시말해,
이 문제는 배열의 모든 원소들이 '자신보다 큰 원소가 왼쪽에 몇개 있는지' 또는, '자신보다 작은 원소가 오른쪽에 몇개 있는지'를 알아내는 문제가 된다.
그리고, 이러한 문제를 해결하기 위한 알고리즘을 바로 Inversion Counting이다.
Inversion Counting
정렬된 상태와 반대된, 역위(Inversion)의 개수를 구하는 알고리즘이다.
segment tree를 이용한 방법과
merge sort를 이용한 방법 2가지가 존재한다고 한다.
segment tree를 이용한 방법의 경우,
배열의 각 원소의 값과 원래 인덱스를 기억한 상태로,
값을 기준으로 배열을 오름차순 정렬하고,
정렬된 배열을 순회하며 segment tree에 인덱스를 저장한다.
배열이 값을 기준으로 오름차순 정렬되어있기 때문에,
트리에 저장된 인덱스가 가르키는 값은 항상 현재 탐색중인 값보다 작다.
따라서, 저장된 인덱스가 현재 탐색중인 값의 인덱스보다 크다면,
정렬되기 전의 원래 배열에서 '현재 값보다 작은 값의 원소가 더 뒤에있는' 상태이기 때문에,
이는 Inversion된 상황으로 간주할 수 있다.
즉, '현재 탐색 대상인 값의 원래 인덱스보다 큰 인덱스의 갯수'를 구해서 계속 더해주면 된다.
세그먼트 트리(Segment Tree)는 배열 간격에 대한 정보를 이진 트리에 저장하는 자료구조로,
tree의 수정과 탐색 모두 이 소요된다.
배열의 각 원소를 탐색할때마다 구간에 존재하는 수의 개수가 바뀌기 때문에,
n번의 수정과 탐색이 일어나므로, 의 시간 복잡도를 갖게된다.
merge sort를 이용한 방법은,
병합(merge)과정에서 정렬된 두 배열을 하나의 배열로 합칠 때 inversion counting을 해주는 방법이다.
과정은 다음과 같은 논리로 일어난다.
- merge 대상인 left array와 right array는 각각 정렬된 상태이다.
- left array의 모든 원소들은 right array보다 왼쪽에 있다.
- left array의 i번째 수가 right array의 j번째 수 보다 크다면,
left array의 i번째 이후(배열의 오른쪽)에 존재하는 모든 수는 right array의 j번째 수보다 크다.- 따라서, right array의 j번째 수를 기준으로 left array의 i번째 이후(배열의 오른쪽)에 존재하는 모든 수는 inversion이 발생한 수 이다.
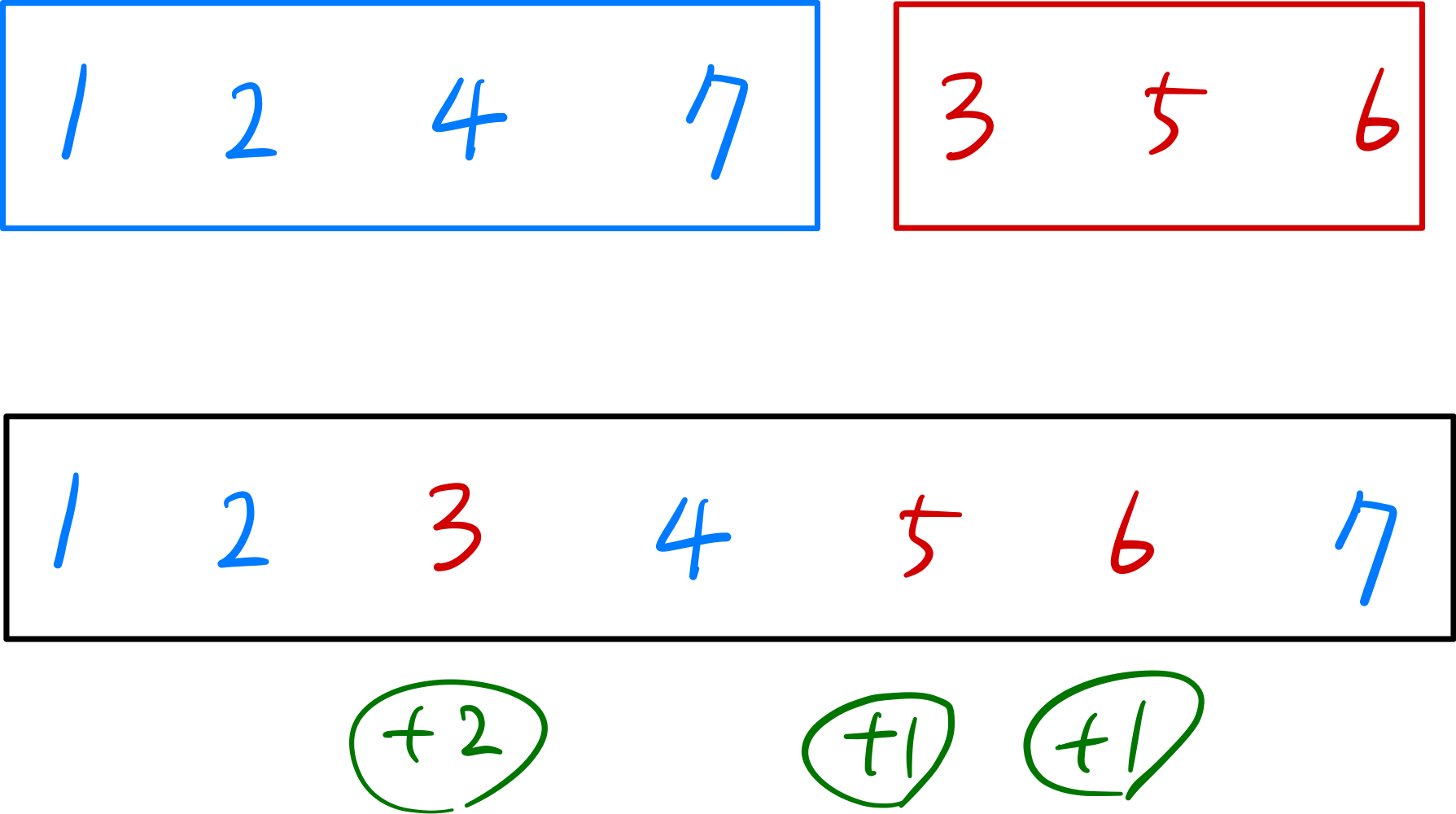
위 그림에서 right array의 3을 예로 들면,
left array에서 3보다 처음으로 큰 수는 left array의 2번째 index에 위치하는 4이다.
left array는 오름차순 정렬된 상태이므로, 4보다 뒤에 나타나는 수들은 모두 4이상의 값을 갖는다.
따라서, 원래 배열인 (1, 2, 4, 7, 3, 5, 6)에서 3보다 크면서 왼쪽에 존재하는 수는 2개이다.
이러한 방식으로 right array의 5, 6 또한 Inversion된 수의 갯수를 확인할 수 있고,
위 예시에서는 총 4개의 inversion을 확인할 수 있다.
위에서 설명했듯, 이는 버블 정렬시의 swap의 발생횟수와 동일하다.
코드
merge sort를 이용한 방법
def solution(N: int, A: list):
answer = 0
sorted_A = [0] * len(A)
answer = merge_sort(0, len(A)-1, A, sorted_A)
return answer
def merge_sort(start, end, arr, result):
mid = (start + end) // 2
if start < end:
cnt = 0
cnt += merge_sort(start, mid, arr, result)
cnt += merge_sort(mid+1, end, arr, result)
return cnt + merge(start, mid, end, arr, result)
return 0
def merge(start, mid, end, arr, result):
p1 = start
p2 = mid+1
idx = start
count = 0
while (p1 <= mid and p2 <= end):
if arr[p1] <= arr[p2]:
result[idx] = arr[p1]
p1 += 1
else:
result[idx] = arr[p2]
count += mid-p1+1 # 1
p2 += 1
idx += 1
while p1 <= mid:
result[idx] = arr[p1]
p1 += 1
idx += 1
while p2 <= end:
result[idx] = arr[p2]
p2 += 1
idx += 1
for i in range(start, end+1):
arr[i] = result[i]
return count
if __name__ == '__main__':
import sys
N = int(sys.stdin.readline().strip())
A = list(map(int, sys.stdin.readline().split()))
ans = solution(N, A)
print(ans)주석 1번
기존 merge sort에서 유의미하게 추가된 단 한줄의 코드이다.
해당 라인을 분기하는 조건문은
'start~mid'의 범위로 정의되는 '왼쪽 배열' 과
'mid+1~end'의 '오른쪽 배열'의 각각의 포인터(인덱스; p1, p2)에서의
대소관계를 비교한다.
else문은 '왼쪽 배열'의 p1위치의 값이 '오른쪽 배열'의 p2위치의 값보다 큰 경우를 의미하며,
따라서 위에서 설명한 대로 '왼쪽 배열'의 p1부터 mid 까지의 값이 오른쪽 배열의 p2위치에 있는 값보다 큰 값들이기 때문에 이들의 갯수를 누적하여 더해준다.
segment tree를 이용한 방법
pypy로 제출해야 시간초과 없이 통과한다.
def solution(N: int, A: list):
answer = 0
tree = [0] * (N * 4)
arr = []
for i in range(N):
arr.append((A[i], i))
arr.sort()
for i in range(N):
index = arr[i][1]
answer += query(1, 0, N-1, index+1, N-1, tree)
update(1, 0, N-1, index, tree)
return answer
def query(current_index, start, end, query_start, query_end, tree):
if end < query_start or query_end < start:
return 0
if query_start <= start and end <= query_end:
return tree[current_index]
mid = (start + end) // 2
left = query(current_index*2, start, mid, query_start, query_end, tree)
right = query(current_index*2+1, mid+1, end, query_start, query_end, tree)
return left + right
def update(current_index, start, end, node_index, tree):
if start == end:
tree[current_index] = 1
return
mid = (start + end)//2
if node_index <= mid:
update(current_index*2, start, mid, node_index, tree)
else:
update(current_index*2+1, mid+1, end, node_index, tree)
tree[current_index] = tree[current_index*2] + tree[current_index*2+1]
if __name__ == '__main__':
import sys
N = int(sys.stdin.readline().strip())
A = list(map(int, sys.stdin.readline().split()))
ans = solution(N, A)
print(ans)주석 1번
이 부분이 바로
'배열의 각 원소의 값과 원래 인덱스를 기억하는 배열을 만드는' 부분이며, 위 코드에서 만들어진 배열의 변수명은 arr이다.
2라인 아래에서 해당 배열을 정렬하며,
이후 다시한번 반복문을 순회하며 arr의 원소를 차례대로 순회하는것을 확인할 수 있다.
주석 2번
반복문을 다시 순회하며, arr의 원소를 차례대로 꺼내어 segment tree에 query와 update을 수행한다.
arr는 값으로 정렬된 상태이므로, query 수행시의 tree에 존재하는 모든 노드가 나타내는 값은 항상 current_index가 나타내는 값 이하이다.
따라서, tree에 존재하며 current_index보다 큰 index를 저장하고 있는 노드가 있다면,
이는 current_index가 가르키는 값보다 크기가 작지만, 원래 배열에서는 더 뒤쪽에 위치하고 있었다는 의미이다.
따라서 query는 이러한 조건의 노드의 갯수를 확인하여 반환하고,
answer에 누적하여 더해준다.
그리고 current_index도 다음 순회의 비교를 위해 tree에 update 해주며 반복문의 한 사이클이 종료된다.
참고
https://frhyme.github.io/algorithms/python_count_inversion_in_lst/
https://barbera.tistory.com/41
