[프로그래머스][Python] 가장 긴 팰린드롬

Hyeon·2023년 2월 21일

코딩테스트

목록 보기

10/44

문제

문제 설명

앞뒤를 뒤집어도 똑같은 문자열을 팰린드롬(palindrome)이라고 합니다.
문자열 s가 주어질 때, s의 부분문자열(Substring)중 가장 긴 팰린드롬의 길이를 return 하는 solution 함수를 완성해 주세요.

예를들면, 문자열 s가 "abcdcba"이면 7을 return하고 "abacde"이면 3을 return합니다.

제한사항

문자열 s의 길이 : 2,500 이하의 자연수
문자열 s는 알파벳 소문자로만 구성

입출력 예

s	answer
"abcdcba"	7
"abacde"	3

입출력 예 설명

입출력 예 #1

4번째자리 'd'를 기준으로 문자열 s 전체가 팰린드롬이 되므로 7을 return합니다.

입출력 예 #2

2번째자리 'b'를 기준으로 "aba"가 팰린드롬이 되므로 3을 return합니다.

접근

이 문제는 문자열의 최대 길이가 2400자로
단순히 문자열의 문자를 하나씩 순회하며, 각 문자를 중심으로 한 팰린드롬 문자열의 최대길이를 구해가면서
최대값을 갱신해도 되는 문제이다. 이러한 방식의 시간복잡도는 $O(n^2)$ 이다.

하지만 분명 더 효율적인 알고리즘이 존재할것이라고 생각되어(문자열 관련 알고리즘은 참 많더라..) 찾아보았고
이번에 알게된 manacher's algorithm을 이용하여 문제를 풀이하였다.

manacher's algorithm

주어진 문자열의 부분문자열 중 가장 긴 팰린드롬 문자열을 구하는것이 문제의 조건이다.
manacher 알고리즘은 다음과 같은 과정을 거쳐 이를 보다 효율적으로 계산하여
$O(n)$ 의 시간복잡도를 가지고 이를 구하는 것이 가능하다.

0. 기본 개념

전체 문자열 S의 문자와 1:1대응하는 배열 A를 선언한다.
A[i]는 S[i]를 중심으로 하는 팰린드롬 반지름의 최대 길이이다.

전체 문자열의 길이만큼 반복문을 순회하며
하나의 문자를 중심으로 한 팰린드롬의 최대길이의 반지름을 구하고
현재 탐색중인 문자 S[k]가 현재까지 구해진 최장 길이의 팰린드롬에 속해있다면,
A[k]의 초기값을 0이상의 수로 초기화 할 수 있다.

1. 패딩(padding)

전체 문자열을 수정하여, 전체 문자열의 시작과 끝, 그리고 각 문자 사이에 패딩을 준다.
예를들어 "banana" 라는 문자열에 '#' 라는 문자로 패딩을 주면 "#b#a#n#a#n#a#" 가 된다.

이는 전체 길이가 짝수인 팰린드롬을 식별하기 위한 하나의 장치로,
manacher 알고리즘의 방식이 현재 탐색중인 문자를 중심으로 하는 팰린드롬이 길이를 구하기 때문이다.
만약 "baab"와 같은 문자열에서는 'a'를 중심으로 팰린드롬을 찾을 수 없게된다.
그러나 이를 "#b#a#a#b#"로 수정하면 가운데에 위치한 '#'을 기준으로 좌우가 같은 문자임을 알 수 있어
제대로 된 팰린드롬의 길이를 구할 수 있다.

또한, 위에서 배열 A에는 팰린드롬의 반지름 길이가 저장된다고 하였는데,
위와 같이 패딩을 주게되면
'패딩을 준 문자열에서 팰린드롬의 반지름 길이'가 곧 '원본 문자열의 팰린드롬 길이'가 되므로
더 직관적인 코드 작성이 가능하다.

2. 중심과 오른쪽 끝

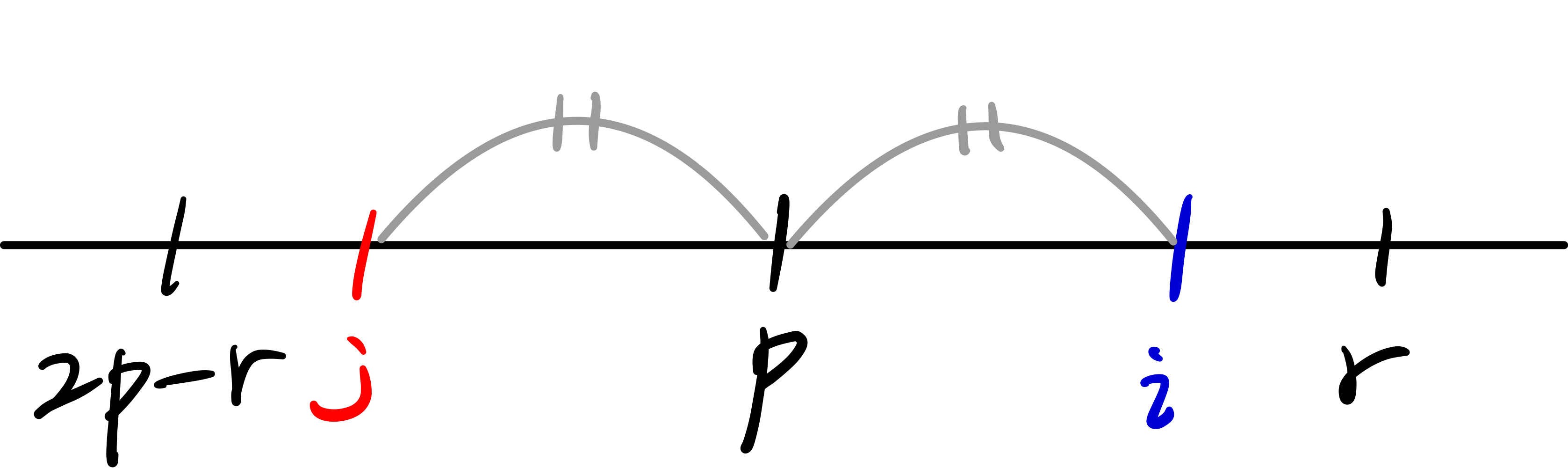
두개의 변수 r, p를 갱신시켜주어야 한다.
r : 오른쪽으로 가장 긴 팰린드롬의 오른쪽 끝 인덱스
p : 오른쪽으로 가장 긴 팰린드롬의 중심 인덱스

3. A[i]의 초기값

두 가지 경우가 존재한다.

1) i $>$ r 인 경우
A[i]의 초기값은 0

2) i $\leq$ r 인 경우
p를 기준으로 i와 대칭점에 있는 인덱스를 j라고 하면,
$j = 2 \times p - i$ 이고,
A[i]의 초기값은 $\min(r-i, A[j])$ 이다.

그 이유는

A[j]가 팰린드롬이 아닐 경우 A[i]도 팰린드롬이 아니다.
A[j]가 팰린드롬일 경우 A[i]도 팰린드롬일 수 있다.
- A[j] $\leq r-i$ 인 경우 A[i]의 초기값은 A[j]
- A[j] $\gt r-i$ 인 경우 A[i]의 초기값은 $r-i$
  - A[j] $\gt r-i$ 라는건
    p의 왼쪽끝을 넘어선 문자들이 j를 중심으로 한 팰린드롬에 포함되어있다는 뜻이며,
    이 문자들이 i를 중심으로 한 팰린드롬에도 포함될 것이라는 보장이 없다.

코드

전체 코드는 다음과 같다.

def solution(s):
    answer = 0
    A = [0] * (2 * len(s) + 1)
    string = ['#', ]
    for i in range(len(s)):
        string.append(s[i])
        string.append('#')
    answer = manacher(string, A)
    return answer


def manacher(string, A):
    N = len(string)
    p = 0
    r = 0

    for i in range(N):
        if i <= r:
            j = 2*p - i
            A[i] = min(r-i, A[j])
        else:
            A[i] = 0

        right = i+A[i]+1
        left = i-A[i]-1
        while 0 <= right < N and 0 <= left < N and string[right] == string[left]:
            A[i] += 1
            right += 1
            left -= 1

        if i + A[i] > r:
            p = i
            r = p + A[p]

    return A[p]

실수

함수 manacher()의 반복문 마지막에 존재하는
p, r을 갱신하는 조건문에서 실수가 있었다.

맞는 코드

if i + A[i] > r:
	p = i
    r = p + A[p]

실수한 코드

if A[i] > A[p]:
	p = i
    r = p + A[p]

실수한 코드로 작성해도 정답은 통과한다.
왜냐하면, 인덱스가 증가하는 방향으로 탐색하기 때문에
항상 $p\leq i$ 이며,
따라서 $A[p] < A[i]$ 이라면
$A[p] + p = r < A[i] + i$ 가 성립하기 때문이다.

하지만, $r < A[i] + i$ 이라고 해서
항상 $A[p] < A[i]$ 이 성립하지는 않기 때문에,
초기값이 제대로 갱신되지 않을 수 있고,
문자열에 따라서 manacher 알고리즘을 제대로 이용하지 못하게 될 수 있다.

예를들어,
현재까지의 최장길이 팰린드롬의 중심 인덱스가 $p'$ ,
오른쪽 끝의 인덱스가 $r'$ 이라고 하고,
현재 탐색중인 인덱스가 $i$ ,
$r'$ 과 $i$ 사이에 두 번째로 긴 팰린드롬이 존재한다고 가정하자.

이 두 번째로 긴 팰린드롬의 중심은 $p''$ , 오른쪽 끝은 $r''$ 이고,
$r$ 과 $r'$ 이 $i$ 에 대해서 각각
$r' < i$
$r'' \geq i$
라고 한다면,

맞는 코드로 작성한 알고리즘은 $r$ 과 $p$ 가 각각 $r''$ , $p''$ 으로 갱신되어있기 때문에
$A[i]$ 의 초기값은 0 이상의 값으로 시작 할 수 있다.

하지만, 실수한 코드로 작성한 알고리즘은 $r$ 과 $p$ 가 $r'$ , $p'$ 인 상태로 존재하므로,
$r < i$ 이며, 이에 따라
$A[i]$ 의 초기값은 항상 0인 상태에서 시작하게 된다.
즉, 최장 길이의 부분 문자열 펠린드롬이 전체 문자열의 앞부분에서 발견된다면,
이후 탐색에서 배열 A의 존재 목적이 사라지게 되고 $O(n^2)$ 의 시간 복잡도를 가지는
반복문을 이용한 방법과 별반 다를 바 없는 연산을 수행하게 된다.