[프로그래머스][Python][2022 Kakao] 양과 늑대

Hyeon·2023년 3월 23일

2022 카카오 알고리즘 카카오 프로그래머스

코딩테스트

목록 보기

42/44

카카오의 해설과 이 블로그의 풀이를 보고 작성하였습니다.

문제

[프로그래머스][Python][2022 Kakao] 양과 늑대

풀이

아무래도 완전 탐색을 해야겠는데,
선택한 양과 늑대를 다시 방문할 수 없는것도 아니고,
시간 초과를 반복하며 고민 하다가 결국 다른 사람의 풀이를 봤다.

1. 카카오 해설 - DFS 완전탐색

이 풀이의 아이디어는 "이미 방문한 정점은 언제든 방문 가능하다"는 접근에서 출발한다.

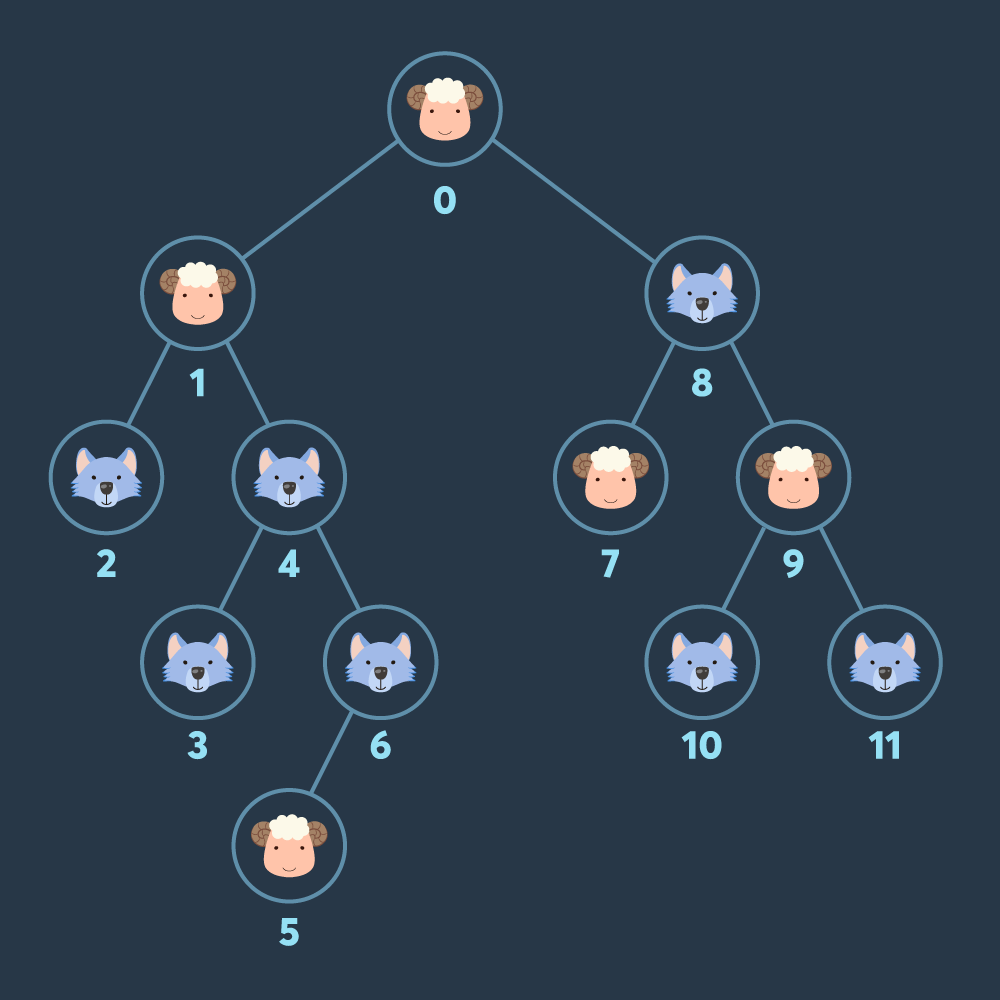
예제 1번을 이용해서 이야기 해보자. 주황색 노드는 양, 검정색 노드는 늑대이다.

0번 노드에서 출발하기 때문에, 1번 노드 또는 8번 노드로 이동할 수 있다.
먼저 1번 노드로 이동했다고 가정하자,
그 다음으로 이동 가능한 노드는 몇번일까?

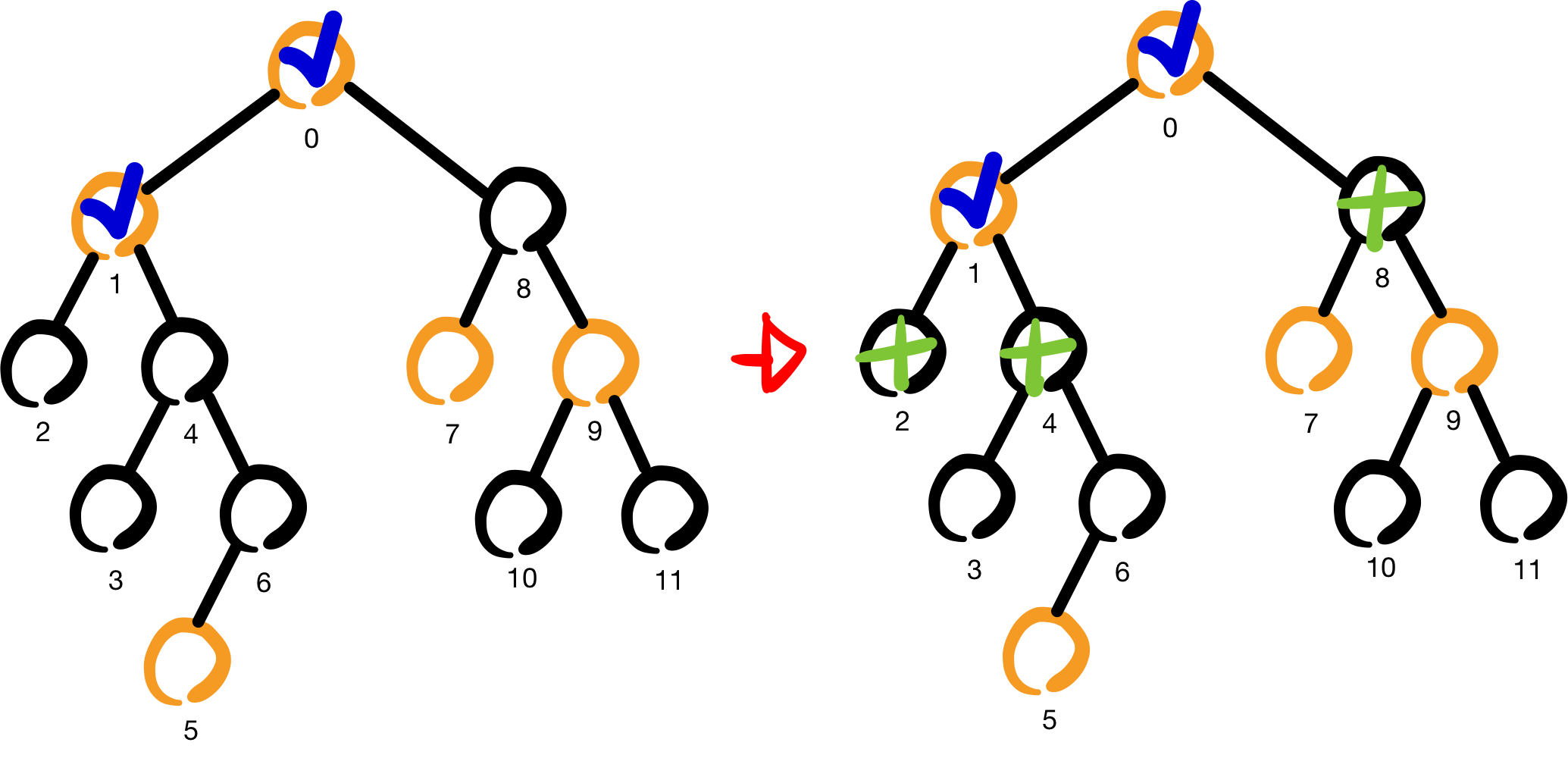
1번 노드의 자식 노드인 2, 4번 뿐만 아니라 8번 노드 또한 방문이 가능하다.
그 이유는 "1번 노드를 방문한 시점에선 0번 노드를 이미 방문했기 때문"이다.

따라서 다시 0번 노드로 되돌아가지 않고도 8번 노드를 방문할 수 있도록 한다면,
꼭 트리의 구조를 따라서 위아래로 이동하며 자식노드만을 완전 탐색하지 않아도 된다.

다시 이동해보자, 이번에는 4번 노드로 이동하겠다.

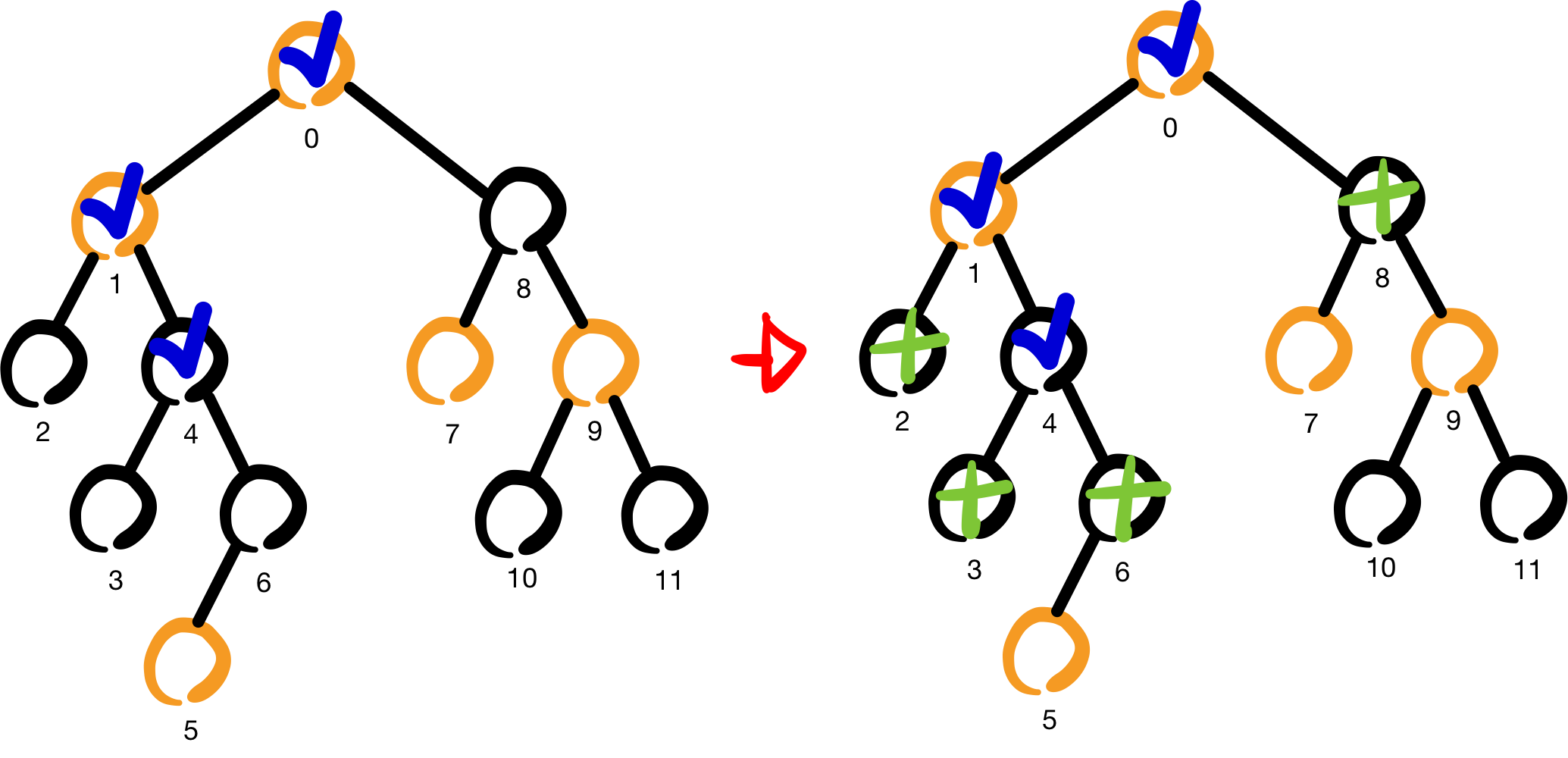
마찬가지로 4번 노드에서 방문할 수 있는 노드는 2, 3, 6, 8의 4개 노드이다.

이 규칙을 다시 정의하면 이렇게 설명 할 수 있다.

현재 방문한 노드의 두 자식 노드는
앞으로 방문할 모든 자손 노드들이 방문 가능한 노드이다.

노드를 방문할 때 그 다음으로 방문 가능한 모든 노드들을 한번에 확인할 수 있고,
"방문 가능하지만 부모노드의 다른 자식 노드이기 때문에 어쩔 수 없이" 다시 부모 노드로 돌아갈 필요 없이 가능한 모든 경우를 탐색할 수 있다.

코드

# https://school.programmers.co.kr/learn/courses/30/lessons/92343

import sys
sys.setrecursionlimit(10**6)

ans = 0

def solution(info, edges):
    # 인접 리스트 생성
    adj = [[] for _ in range(len(info))]
    for i in range(len(edges)):
        adj[edges[i][0]].append(edges[i][1])
    
    # 방문 가능한 노드들을 담을 리스트 생성
    nodes = []

    solve(0, nodes, adj, 0, 0, info)
    return ans

def solve(current:int, nodes:list, adj:list, sheep:int, wolf:int, info:list):
    global ans
    
    # 현재 방문한 노드에 따라 양 또는 늑대 수 증가
    sheep += info[current] ^ 1
    wolf += info[current]

    # 현재 양의 수가 최대값보다 크다면 갱신
    ans = max(ans, sheep)

    # 만약 늑대의 수가 양의 수보다 같거나 크면 종료
    if sheep <= wolf:   return
    
    # 현재 방문한 노드의 두 자식 노드는
    # 앞으로 방문할 모든 자손 노드들이 방문 가능한 노드이다.
    for i in adj[current]:
        nodes.append(i)

    # 방문 가능한 노드를 순회하며 재귀호출
    # 이때, 방문 대상인 노드는 방문 가능한 노드 목록(nodes)에서 제외해야함.
    # 또한, nodes는 함수가 호출될 때 마다 독립적으로 존재해야함(deep copy)
    for i in range(len(nodes)):
        next = nodes[i]
        solve(next, nodes[:i]+nodes[i+1:], adj, sheep, wolf, info)

2. 이 블로그(바킹독 님)의 해설

이분이 제기한 문제는, DFS를 이용한 백트래킹 완전탐색 방식이 Complete Binary Tree 형태에서 시간 초과가 발생한다는 것.

카카오가 문제의 난이도를 위해 일부러 TC를 여유있게 주었든, 의도치 않은 문제의 허점이든 간에
공부할 필요가 있어 보이는 내용이라고 생각되어 정리한다.

상태의 중복 - 피보나치 함수의 예

"피보나치를 재귀 함수로 구현할 때와 마찬가지로, 상태의 중복으로 인해 시간 복잡도가 증가한다."

우선 여기서 말하는 재귀 함수로 구현한 피보나치는, 아마 아래와 같은 코드를 의미할 것이다.

def fibo(n):
	if n < 2: return n
	return fibo(n-1) + fibo(n-2)

이 방식의 문제점은 뭘까? 바로 중복된 부분문제를 해결하기 위해 계속해서 재귀 호출을 반복한다는 것이다.
매 호출마다 2번의 재귀 호출을 반복하므로, $O(2^n)$ 의 시간 복잡도를 갖는다.

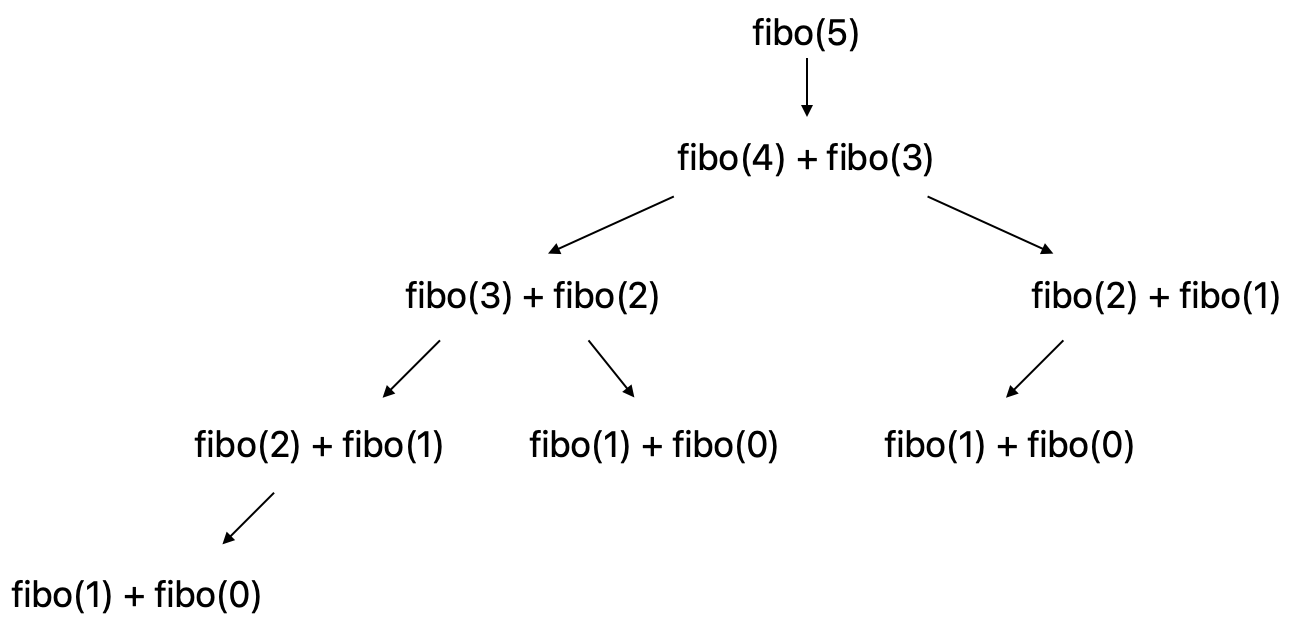
그리고 이 문제를 해결하기 위한 기술은 메모이제이션.
중복되는 부분문제를 처리할 때, 아직 해결한 적 없는 부분문제라면 계산해서 기억하고, 이미 해결된 부분문제라면 이전에 계산한 값을 이용하는 것이다.

바로 아래와 같은 코드이다.

def fibo(n):
    cache = [-1] * (n+1)
    
    def _fibo(n):
        if n < 2:
            return n
        if cache[n] != -1:
            return cache[n]
        cache[n] = _fibo(n-1) + _fibo(n-2)
        return cache[n]
        
    return _fibo(n)

cache라는 배열을 선언하고, 2개의 기저 사례를 통해 재귀 호출을 종료한다.
하나는 이전과 동일하게 2 미만일 경우에는 n을 반환해주는 것
다른 하나는 cache[n]이 -1이 아닐 때 cache[n]을 반환하는 것 이다.

cache[n]은 선언과 함께 모든 값이 -1로 초기화 되었기 때문에,
"cache[n]이 -1이 아닌 경우" 라는 조건은 해당 배열의 원소가 다른 값으로 갱신되었다는 의미이다.

이러한 갱신은 2가지의 기저 사례에 해당 하지 않는 경우에서 발생하는데,
재귀 호출을 통해 계산된 결과를 cache 배열에 저장하는 것을 확인할 수 있다.

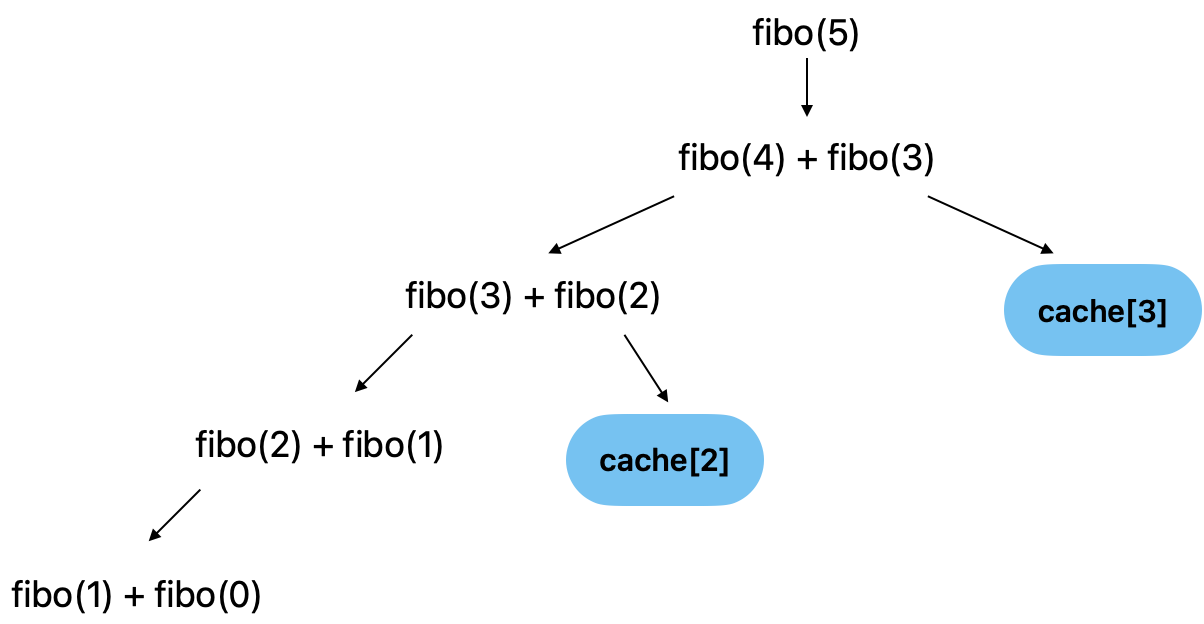
즉, cache를 이용해서 계산된 부분 문제를 기억하고, 부분 문제의 해가 중복되어 필요할 경우엔 다시 재귀 호출을 반복하는 것이 아니라 기억한 값을 즉시 꺼내어 주는것이 가능하며, 이에 따라 시간 복잡도가 $O(n)$ 으로 감소한다.

정리하면, 중복되는 부분문제를 계산하기 위해 재귀 호출을 반복하는, 중복되는 상태를 메모이제이션으로 개선할 수 있다.

상태의 중복 - 본 문제의 경우

다시 문제로 돌아와서, 이 문제를 DFS 완전 탐색으로 풀이할 경우 이러한 상태의 중복이 어떻게 발생한다는 것일까?

먼저 이 문제에서 상태라고 할 수 있는것은 무엇일까? 바로 방문한 노드의 집합이다.
아래 그림을 보자

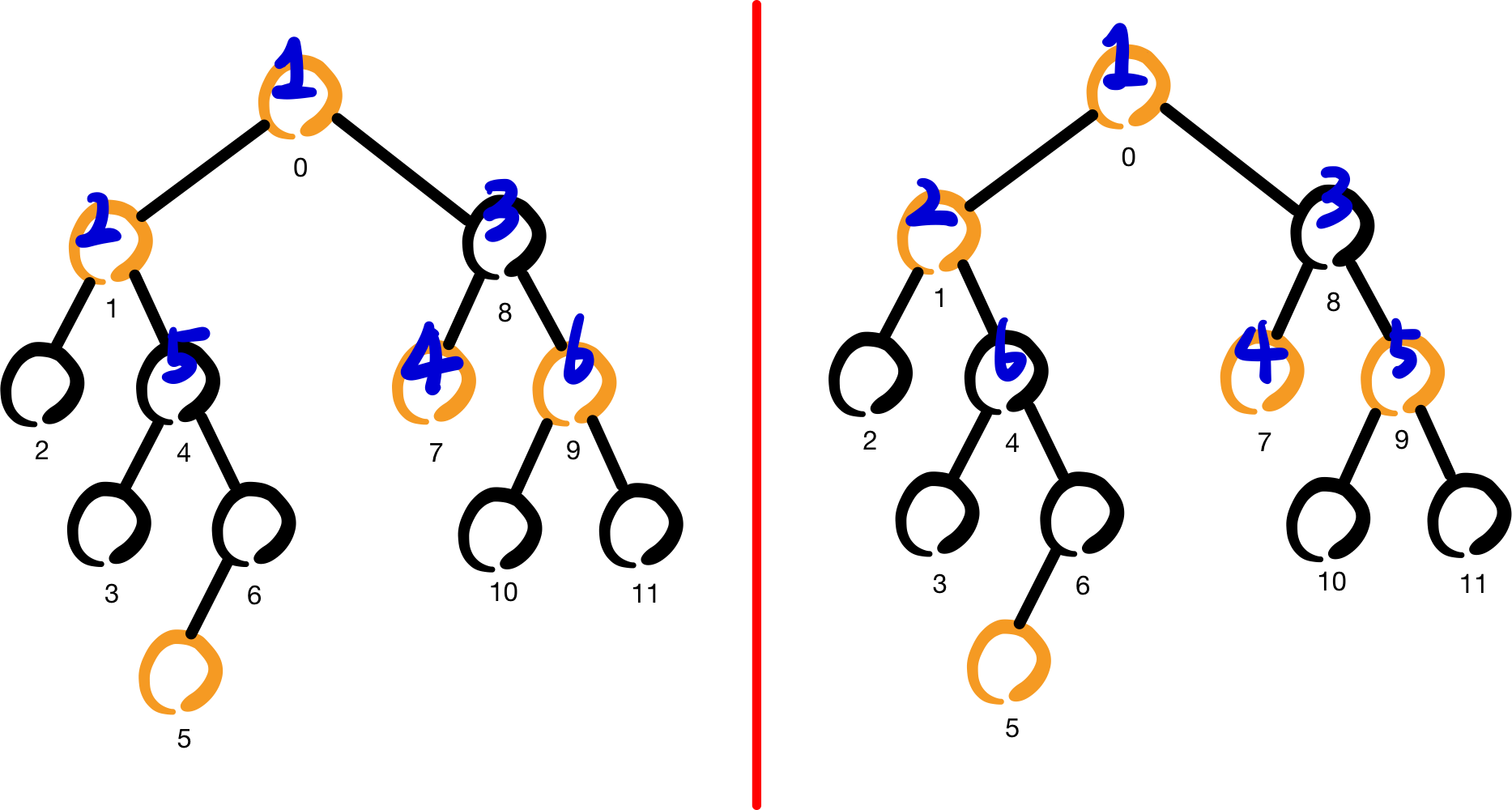
두 그림 모두 똑같은 6개의 노드를 방문한 "상태" 이다.
그러나 방문 순서가 서로 다르다.
좌측: 0 $\rarr$ 1 $\rarr$ 8 $\rarr$ 7 $\rarr$ 4 $\rarr$ 9
우측: 0 $\rarr$ 1 $\rarr$ 8 $\rarr$ 7 $\rarr$ 9 $\rarr$ 4

그런데 이 문제에서 같은 노드 집합을 방문할 때 방문 순서가 의미 있을까? 없다.
왼쪽이나 오른쪽이나 모두 양4마리에 늑대2마리를 달고(?) 다니며
이후에 방문 가능한 노드 또한 모두 같다.
즉, 두 상태는 적어도 문제의 조건하에 같은 상태라고 할 수 있다.

그러면 DFS 백트래킹을 이용한 완전 탐색 풀이는 상태의 중복을 허용하는가?
코드를 다시 보자

def solve(current:int, nodes:list, adj:list, sheep:int, wolf:int, info:list):
    global ans
    
    ''' ... 생략 ... '''

    for i in adj[current]:
        nodes.append(i)
	
    for i in range(len(nodes)):
        next = nodes[i]
        solve(next, nodes[:i]+nodes[i+1:], adj, sheep, wolf, info)

단지 이후에 방문 가능한 노드들을 순회하며 재귀 호출을 반복할 뿐,
같은 노드 집합을 다른 순서로 방문하는 경우에 대해 처리하지 않는다.

상태의 중복을 기억하기 - bit mask

결국 동일한 상태를 다시 확인하는 시도를 반복하지 않으려면,
이를 기억해야한다.

이 문제에서 '동일한 상태'란 방문한 노드의 집합이며,
최대 17개의 노드가 입력으로 주어지므로 정수타입의 비트 마스크로 표현이 가능하다.

ans = 0

def solution(info, edges):
    size = len(info)
    adj = [[] for _ in range(size)]
    visited = [False] * (1<<size)
    for i in range(len(edges)):
        v, u = edges[i]
        adj[v].append(u)
    solve(visited, 1, info, adj)
    return ans

def solve(visited, state, info, adj):
    global ans

    # 현재 상태를 이미 방문한 적이 있는 경우 종료
    if visited[state]:
        return None
    
    # 방문한 적 없는 경우 방문 체크
    visited[state] = True

    # 현재 상태의 양, 늑대 수 확인
    sheep, wolf = 0, 0
    for i in range(len(info)):
        if state & (1<<i):
            wolf += info[i]
            sheep += info[i] ^ 1
    
    # 늑대가 양보다 많거나 같으면 종료
    if sheep <= wolf:
        return None
    
    # 최대값 갱신
    ans = max(ans, sheep)

    # 현재 상태에서 방문 가능한 노드를 순회하며 재귀 호출
    for i in range(len(info)):
        if not (state & (1<<i)):
            continue
        for next in adj[i]:
            solve(visited, state | (1<<next), info, adj)