BOJ 9084 동전

문제 : 동전

✅생각

입력받은 여러 종류의 동전이 있다.
그 중 하나의 동전으로 특정 금액을 만드는 경우는
그 동전을 사용하는 경우와
사용하지 않는 경우가 존재한다.

목표 금액을 만들 수 있는 경우의 수를 구해주기 위해서
만들어줄 수 있는 최소 금액부터 목표금액까지
각 동전으로 만들 수 있는 경우의 수를 누적하며 계산할 것이다.

이를 위해
1원 부터 주어진 목표금액을 열의 길이로,
주어진 동전의 각 순서를 행으로 하는 2차원 배열을 만들어준다.

배열의 각 칸에는
행번호에 해당하는 동전으로,
열번호에 해당하는 금액을 만드는 경우의 수가 들어갈 것이다.

2원 동전부터 채워보자

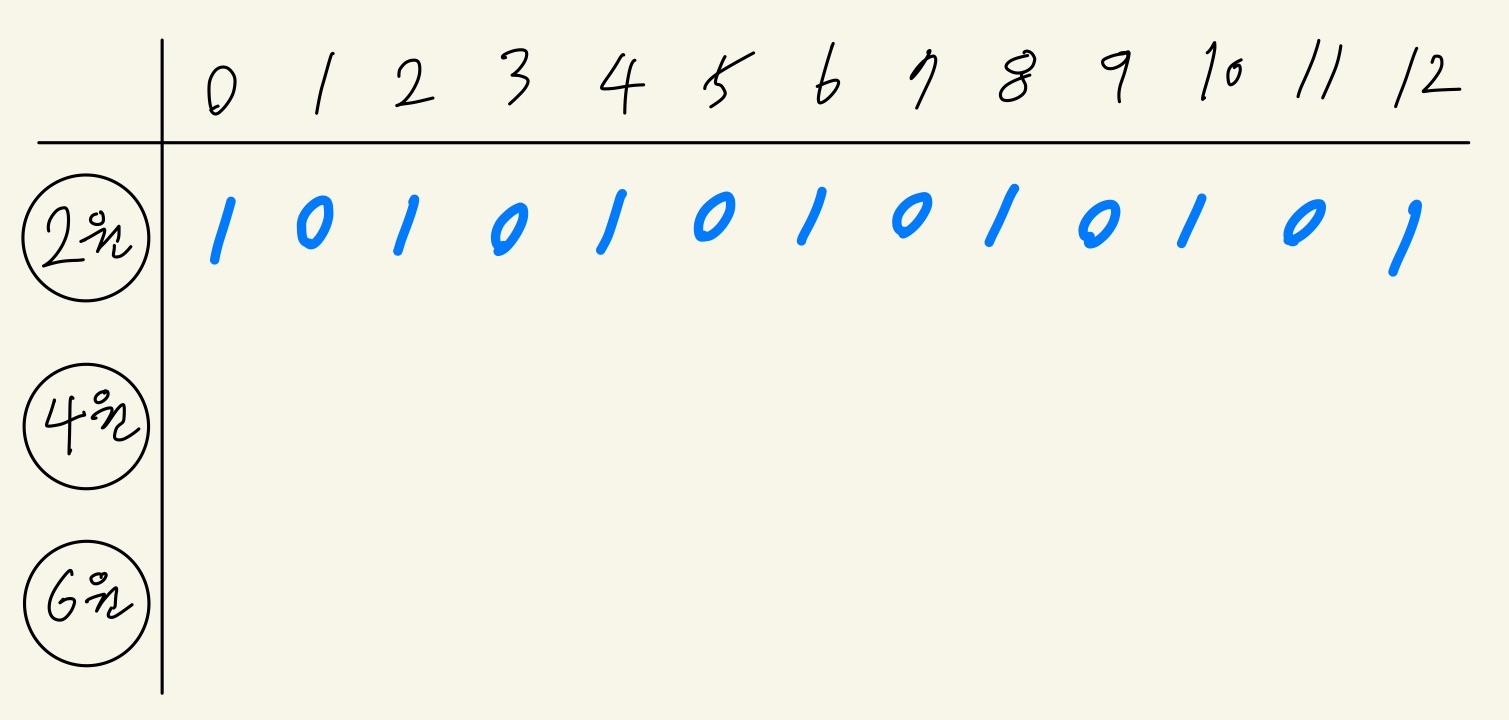
2원 동전으로 만들어줄 수 있는 금액은 2, 4, 6, 8.. 원이 있다.
각 동전을 사용하지 않는 경우에, 0원이므로
0원을 만들어줄 수 있는 경우의 수는 항상 1이다.

그 다음, 4원 동전으로 만들어 줄 수 있는 경우의 수를 구해보자
다만, 경우의 수를 계속 누적해서 갱신할 것이기 때문에
위에서 만들어준 각 금액을 2원 동전으로 만드는 경우의 수를 이용해야 한다.

그러니까 사실 4원 동전행에 있는 경우의 수는
4원 동전 뿐만 아니라 이전에 사용한 동전들의 경우의 수가 누적된,
" 첫번째 동전 ~ 현재 동전인 4원 동전 을 사용해서
해당 금액을 만들어줄 수 있는 경우의 수 " 가 저장된다.

일단 4원 미만의 금액은4원 동전으로 만들어 줄 수 없기 때문에,
"4원 동전을 사용하지 않는 경우" 인
이전까지의 동전으로 만들어준 경우의 수를 가져온다.

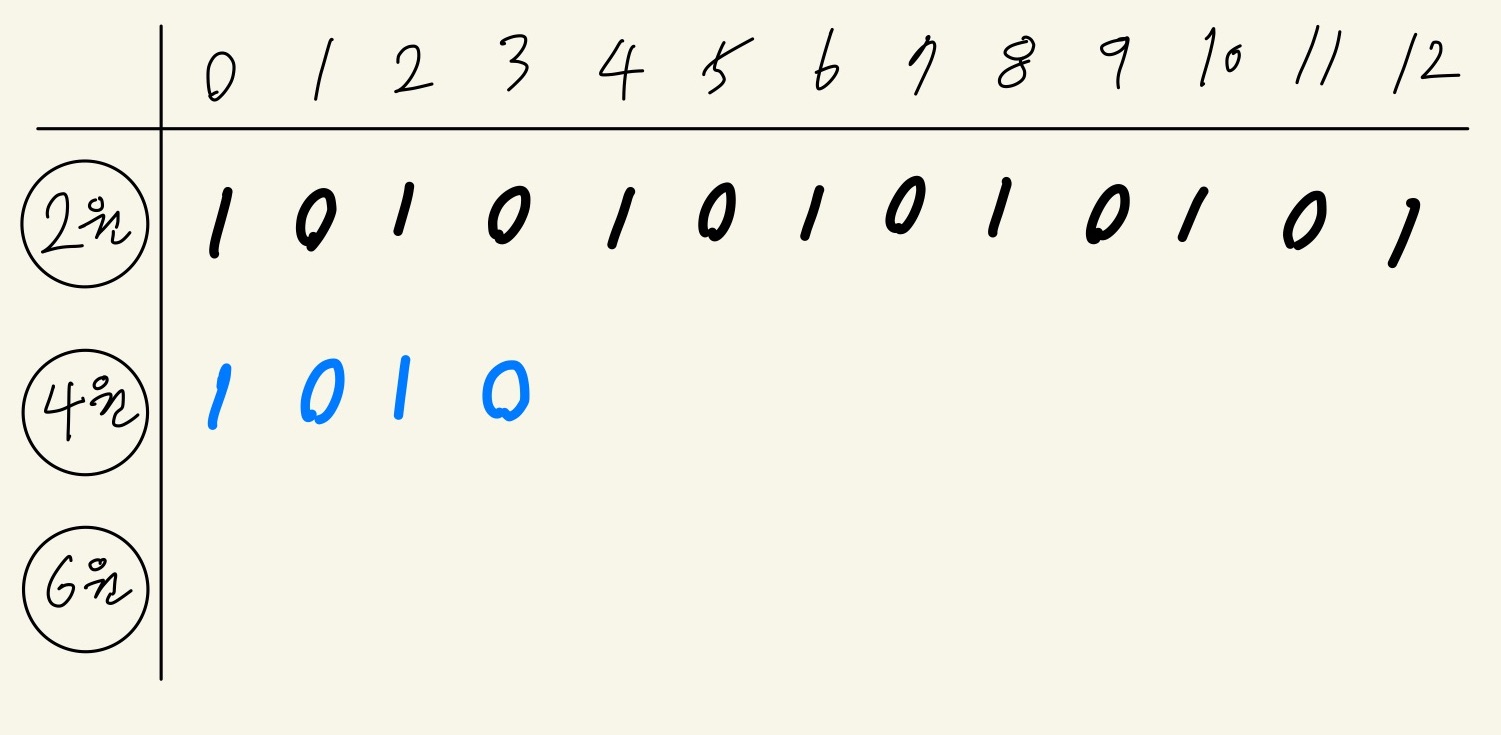
4원 이상 금액부터는 4원 동전을 사용할 수 있기 때문에
"4원 동전을 사용하지 않는 경우" 와
"4원 동전을 사용하는 경우" 두가지 경우의 수를 더해주어야 한다.

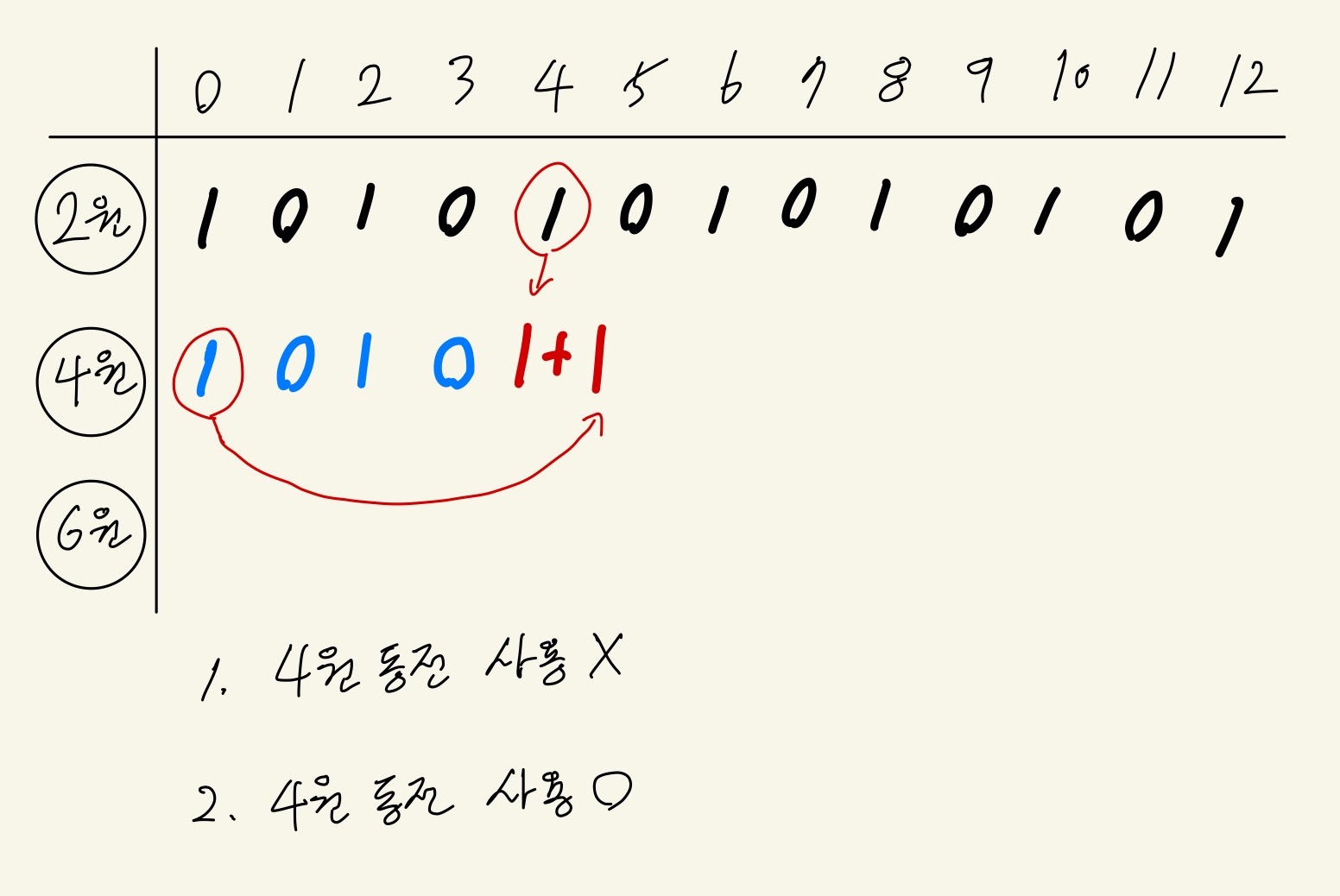
4원 이라는 금액을 만들어줄 때,
"4원 동전을 사용하지 않는 경우" 는
"이전까지의 동전만 사용해서 4원을 만든 경우" 이다.
지금 까지 누적된, 금액 4원에 대한 경우의 수는 $1$ 이므로,
이때의 경우의 수는 1이다.

"4원 동전을 사용하는 경우" 는
4원 동전을 사용했기 때문에,
만들어주려는 금액 4원에서 4원 동전의 가치인 4원을 빼준 값인
0원을 만들어주는 경우의 수와 같다.
따라서 이때의 경우의 수는 $1$이다.

따라서 2원 동전~4원 동전으로 금액 4원을 만들어줄 수 있는 경우의 수는 $2$이다.

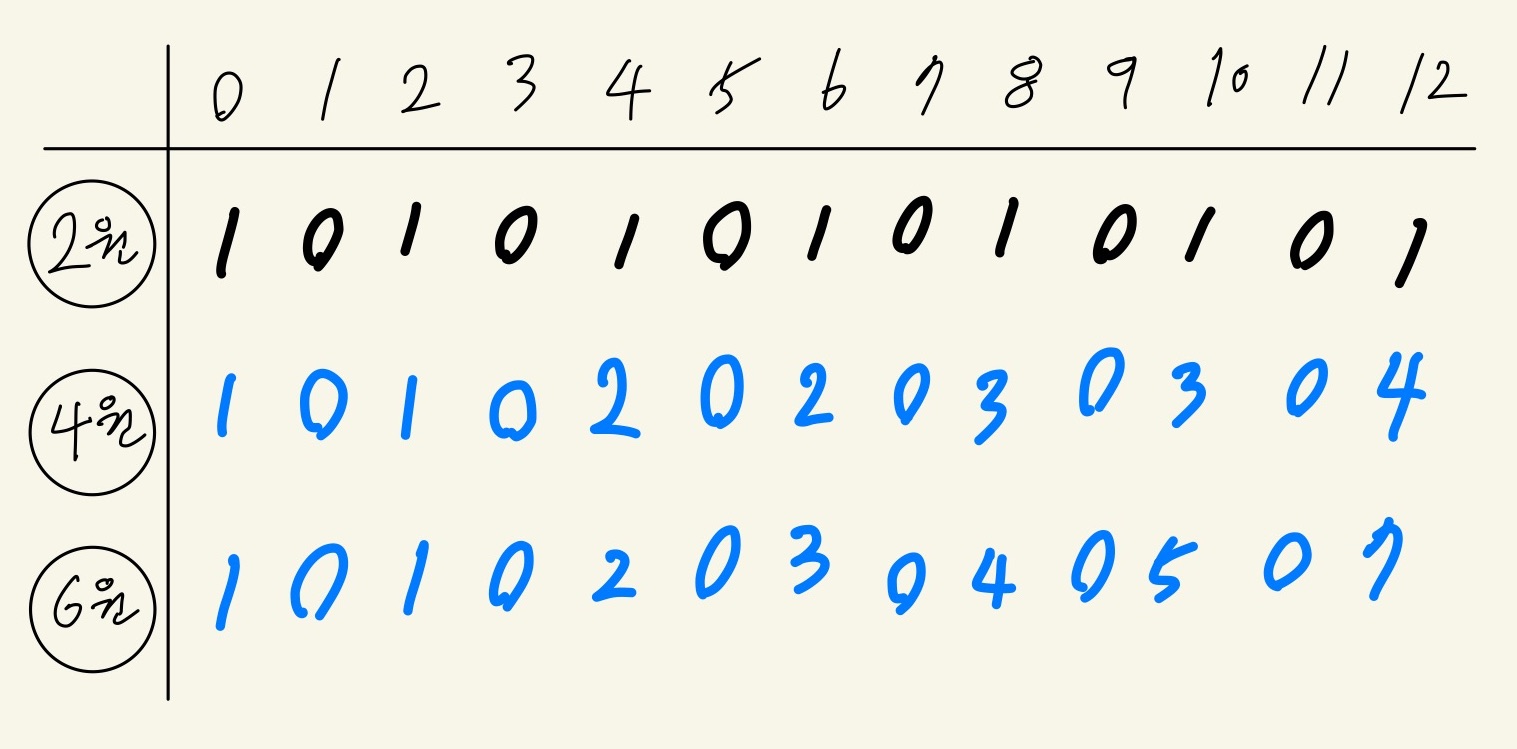
이후의 과정도 동일하게 진행된다.

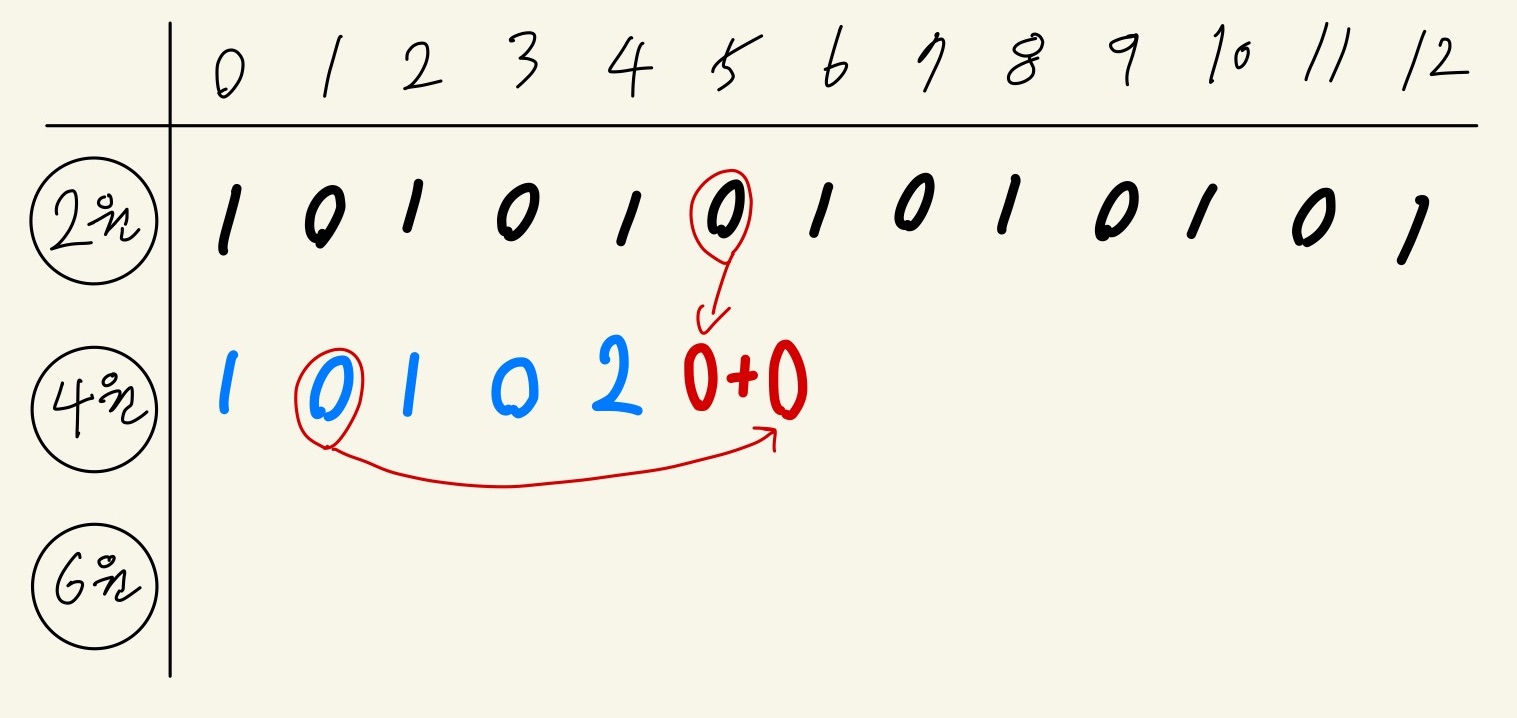
4원 동전 사용 X : 0
4원 동전 사용 O = 금액 5원 - 동전 가치 4원 = 1원 만드는 경우의 수 : 0
0 + 0 = 0

같은 방법으로 경우의 수를 계산하면, 아래와 같다.

📍 정리

1. 현재 동전을 사용하지 않을 때의 경우의 수
   : 이전까지 누적된, 현재 금액을 만드는 경우의 수

2. 현재 동전을 사용할 때의 경우의 수
   : ( 현재 금액 - 현재 동전 가치 ) 를 만드는 경우의 수
   0 미만의 금액을 만드는 경우의 수는 항상 0
   0 원을 만드는 경우의 수는 항상 1

구현

2차원 리스트

위의 배열을 그대로 만들어서 구현했다.

import sys

input = sys.stdin.readline
print = sys.stdout.write

tc = int(input().rstrip())

while tc > 0:
    n = int(input().rstrip())
    tmp = list(map(int, input().split()))
    m = int(input().rstrip())
    coin = []
    for t in tmp:
        if t > m:
            break
        coin.append(t)

    n = len(coin)

    dp = [[0] * (m+1) for _ in range(n+1)]
    for i in range(1, n+1):
        dp[i][0] = 1                    # 현재 동전을 사용하지 않는 경우의 수
        cur_cost = coin[i-1]
        for j in range(1, m+1):
            dp[i][j] = dp[i-1][j]               # 이전 동전으로 계산된 경우의 수를 그대로 내려줌
            if j >= cur_cost:                   # 현재 동전값 이상인 금액에 대해서
                dp[i][j] += dp[i][j-cur_cost]   # 현재 동전을 사용해서 해당 금액을 만드는 경우의 수를 더해줌

    print(f"{dp[n][m]}\n")
    tc -= 1

1차원 리스트

하나의 동전으로 만들어주는 경우의 수를 누적하며 계산하고
누적된 이전 동전의 경우의 수는 다시 사용되지 않는다.

따라서 2차원이 아닌 1차원 리스트로도 구현이 가능하다.

# 동전

# 이전에 계산된 각 금액에 대한 경우의 수는 누적해서 갱신되므로
# dp를 1차원 리스트로 선언해서 
# 현재 순회중인 동전을 이용한 경우의 수를 매 순회마다 누적한다면
# 결국 주어진 금액을 만들기 위한 경우의 수를 구할 수 있음
import sys

def main():
    input = sys.stdin.readline
    print = sys.stdout.write

    tc = int(input().rstrip())
    while tc > 0:
        n = int(input().rstrip())
        coin = list(map(int, input().split()))
        m = int(input().rstrip())

        dp = [0] * (m+1)
        dp[0] = 1

        for c in coin:
            for j in range(c, m+1):
                dp[j] += dp[j-c]

        print(f"{dp[m]}\n")
        tc -= 1

main()