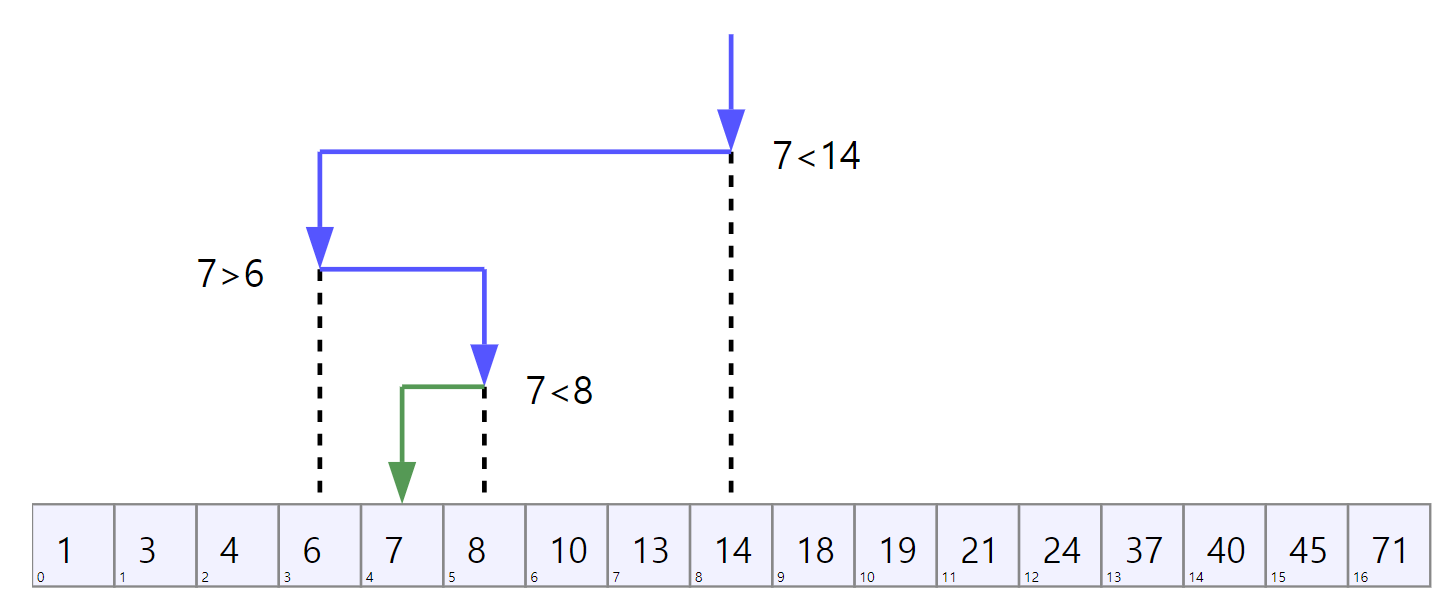
이분탐색 알고리즘을 쓰다보면 직접구현해야하는 경우가 생기기도 하고 라이브러리대신 이정도는 직접 구현해보고 싶은 생각이 드는데, 직접 구현할 때 마다 매번 드는 고민이 있다.. (이분탐색 관련 라이브러리가 없는 언어들은 직접 구현 해야만한다.)
start(left), end(right) 를 정할때 어디까지 정해야하지..?
retrun 을 s를 해야하나? e를 해야하나?
- while start <= end: ... return start ?
- while start < end: ... return end ?
어떤게 맞는거지..?
구현하여 알고리즘 문제들에 코드를 돌려보면 맞는 경우도 있다. (보이는 테스트케이스만)
이런 경우 왜 틀리는건지 제대로 이분탐색을 알고 가야할 필요가 있어 정리를 해보겠습니다.
이분탐색 off-by-one Error(OBOE) 바로알기
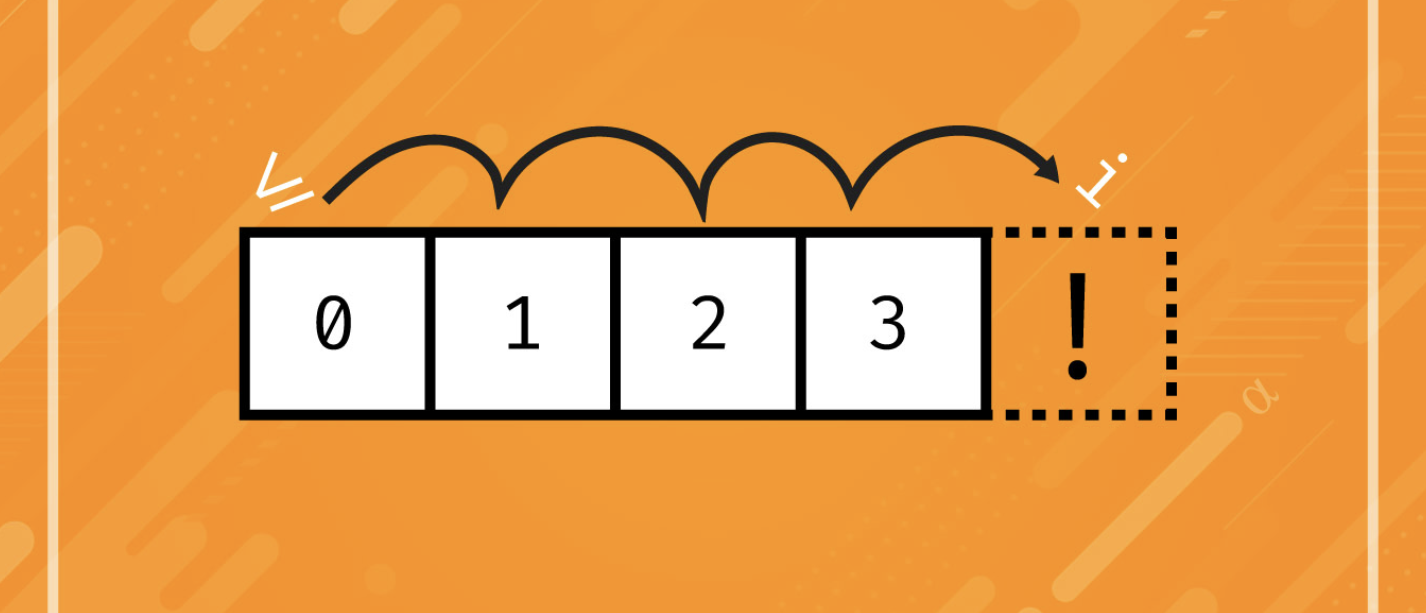
이분탐색 진행시 사실 저희가 위같은 고민을 하게 되는 이유는 바로 off-by-one Error 가 발생하기 쉽기 떄문입니다. 쉽게 말해 while 문 or 재귀함수로 이분탐색을 구현하게 될텐데 while 문의 반복이 한번 더 동작하거나 한번 덜 동작하게 될때 문제가 발생하게 됩니다.
그렇기 때문에 이분탐색 구현을 고려할 때 현재 상황에 맞춰 적절한 탐색이 필요하게 됩니다. "나는 라이브러리를 써서 문제를 해결했으니까 필요 없어" 라는 생각도 위험합니다. 추후 중복값이 나오게되거나, 리스트안에 target value 가 없을 경우 라이브러리 로직에 따라 엉뚱한 값을 return 시킬 수도 있습니다.
여러가지 케이스로 알아보기
python 의 bisect 라이브러리에서 bisect_left, bisect_right 는 내부 동작 구조가 c++ 의 lower_bound, upper_bound 와 매우 유사합니다. 정확한 소스코드를 까보진 않아 내부 동작이 일치한다고 할 순 없으나 유사하여 동일시하게 바라본다면, 제가 공부했을 때 기준으로
bisect_left(lower_bound) 는 이상, bisect_right(upper_bound) 는 초과 로 기억하며 공부했었던 것 같습니다.
사실 이 부분 때문에 off-by-one error 가 발생 했을 확률이 높지만, 다른 케이스도 있습니다. 3가지 예시를 보며 구분해보겠습니다.
- 중복 x, target 은 arr 안에 존재 o | target = 3, target index 를 찾기

# 1. bisect_left(lower_bound) 활용
from bisect import bisect_left
result = bisect_left(arr, target)
print(result) # 2
# 2. 직접 구현
def bs(array, target):
left, right = 0, len(array) - 1
while left <= right:
mid = (left + right) // 2
if array[mid] == target:
return mid
elif array[mid] < target:
left = mid + 1
else:
right = mid - 1
return left
result = bs(arr, target)
print(result) # 2
- 중복 x, target 이 arr 안에 확신 x | target = 3, target index 찾기
(만약 target이 arr 안에 없다면 => -1 출력)
# 1. bisect_left(lower_bound) 활용
'''
bisect_left(lower_bound), bisect_right(upper_bound) 의 경우
target이 없다고 해도 target 보다 큰 가장 최소 value index 를 찾아 return 시키기 때문에
bisect_left or bisect_right 를 활용하여 문제를 풀고 싶다면 값을 재확인 해야함
'''
from bisect import bisect_left
index = bisect_left(arr, target)
result = index if arr[index] == target else -1
print(result)
# 2. 직접 구현
def bs(array, target):
left, right = 0, len(array) - 1
while left <= right:
mid = (left + right) // 2
if array[mid] == target:
return mid
elif array[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
result = bs(arr, target)
print(result) # -1
- 중복 o, target 이 arr 안에 확신 x | target = 3, target 보다 작은 값 개수 세기

# 1. bisect_left(lower_bound) 활용
'''
bisect_left(lower_bound), bisect_right(upper_bound) 로 문제 푸는 것이 오히려 효과적인 case
단, bisect_left(lower_bound) 는 이상인 첫번째 index return
bisect_right(upper_bound) 는 초과하는 인덱스 return 임을 기억하기
'''
from bisect import bisect_left
result = bisect_left(arr, target)
print(result) # 2
# 2. 직접 구현
'''
중복이 허용될 경우 array 안에 target 값이 여러개 들어가 있을 수 있으므로
if array[mid] == target : 시 return 을 하게되면 중복된 값들로 인해
어떤 index 가 리턴될지 모르기에 삭제
범위를 아래처럼 array[mid] < target 과 array[mid] <= target 의 차이는
bisect_left(lower_bound), bisect_right(upper_bound) 차이가 된다.
'''
def bs(array, target):
left, right = 0, len(array) - 1
while left <= right:
mid = (left + right) // 2
if array[mid] < target:
left = mid + 1
else:
right = mid - 1
return left
result = bs(arr, target)
print(result) # 2
마무리
암기한다고 해봤자 금방 잊어버리게되고 범위에 대해서 모호하다면 예시 테스트 케이스를 내가 먼저 작성하고 원하는 범위를 찾아보는 방식이 더 편할 수 도 있다. 직접 구현이 어렵다면 python 의 bisect_left/bisect_right, c++ 의 std::lower_bound/std::upper_bound 를 이용하는 것이 더 편한 방법이 될 수 있다. 그러나 내부 동작이 어떻게 되는지는 반드시 확인 후 사용해야 변칙에 대비할 수 있을 것 같다.
출처 : https://www.acmicpc.net/blog/view/109
출처 : https://www.alpharithms.com/off-by-one-errors-oboe-525118/
출처 : https://school.programmers.co.kr/learn/courses/30/lessons/258709
출처 : https://jetalog.net/112
