본 문제는 프로그래머스 문제로 문제 설명과 TC 에 대해서는 자세히 다루지 않겠습니다. 문제 페이지에서 참고해주세요.
이 글에는 하단에 정답 코드가 포함되어있습니다.
또한 이 문제는 카카오 공식해설이 있는 문제입니다. 해당 해설을 보시는 것도 추천드립니다.
접근 방식
시간복잡도 계산
사실 이 문제를 처음 접했을 때, 모든 사람이 풀이 방식을 떠올릴 수 있지만 시간복잡도 문제를 해결할 방법을 찾는것이 어려운 문제입니다.
- 제한사항
1 ≤ board의 행의 길이 (= N) ≤ 1,000
1 ≤ board의 열의 길이 (= M) ≤ 1,000
1 ≤ board의 원소 (각 건물의 내구도) ≤ 1,000
1 ≤ skill의 행의 길이 ≤ 250,000
우선 브루트포스 방식으로 모든 스킬마다 board 값을 업데이트한다고 가정해 보고 시간복잡도를 계산하면 O(N x M x skill)
즉 1,000,000 * 250,000 = 250,000,000,000 이겠군요,
많은 분들이 프로그래머스 python runtime 동작 기준 대략 1초에 20,000,000 번 연산을 한다고 가정하기에 (pypi 나 python 버전에따라 다르기에 ide 에서 돌려보시는 것은 정확하지 않을 수 있습니다.)
이미 10초라는 시간은 아득히 뛰어넘었습니다.
시간복잡도 개선
제가 시간복잡도 문제를 해결할 때 가장 먼저 생각하는건 연산량을 개선할 수 있는 부분을 찾는 것입니다.
위 문제를 보면 O(N x M x skill) 에서 skill 은 모두 적용해야 하기에 skill 의 연산량 250,000 은 개선할 수 없습니다. 반드시 연산해야하는 양입니다.
10초의 시간(연산량 기준 200,000,000 번)이 저희에게 주어져있고
200,000,000 / 250,000 = 800 입니다.
N 과 M 은 모두 1000 까지 이므로 행, 열 한 사이클조차 돌 수 없습니다.
즉 연산량을 곱이 아닌 합으로 바꿔야하는 문제입니다.
그렇다면 1,000,000 (N*M) + 250,000 = 1,250,000
skill 과 board 연산만 분리하여 합으로만 바꾼다면 추가적인 연산이 조금 있어도 넉넉하게 통과됩니다.
문제 해결 접근
자 이제 시간 복잡도를 어떻게 해결해야 하는 문제인지는 파악했습니다.
그렇다면 어떻게 skill 을 board 와 별개로 분리할지 생각해보다 우선 행, 열 모두 생각하기보다 행에만 집중하였습니다. 행만 개선된다면 열은 같은 원리로 해결할 수 있을 것입니다.
가장 먼저 한 행의 시간복잡도 문제에서 자주 사용되는 알고리즘은 dp와 누적합, 투포인터 등이 있습니다. dp 와 투포인터도 고민해 보았지만 아이디어가 떠오르지 않았고 누적합으로 접근해보았습니다.
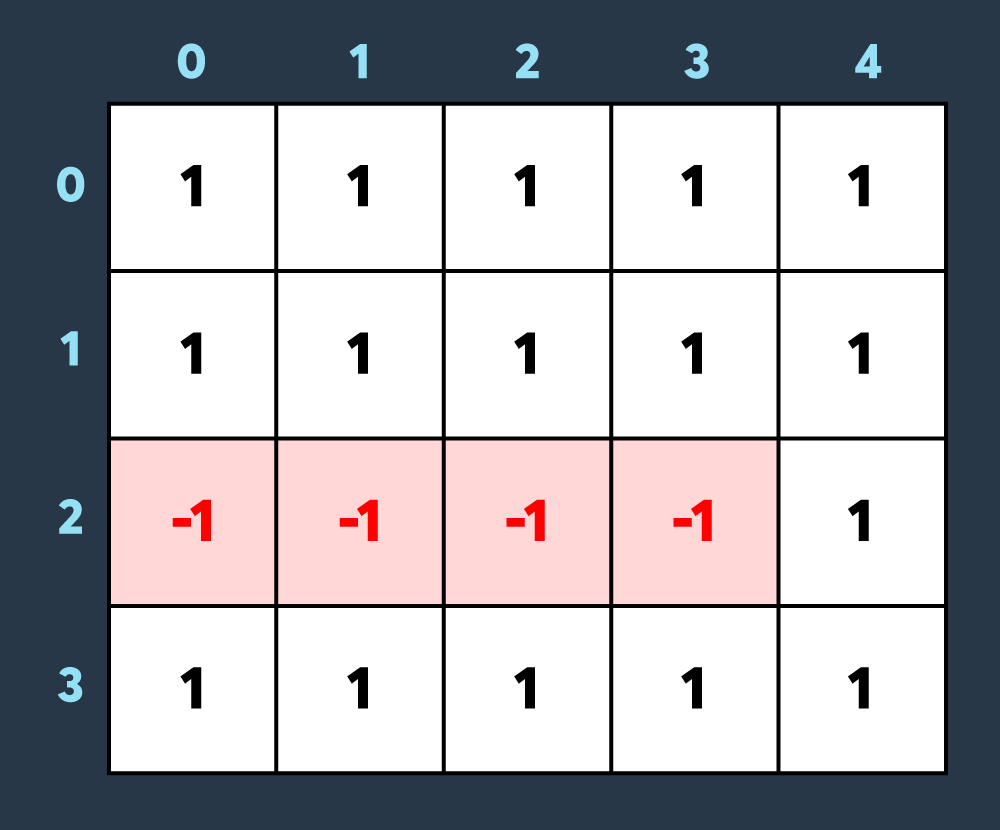
위 그림의 2행처럼 범위의 -2 데미지를 입힌다고 할때
기존 [1, 1, 1, 1, 1] -> [-1, -1, -1, -1, 1] 로 업데이트 되어야하기에 해당 행의 데미지 배열은 [-2, -2, -2, -2, 0] 입니다.
이를 누적합 알고리즘적으로 보자면 [-2, 0, 0, 0, 2]
로 볼 수 있습니다. 위 행을 누적합 시키면 [-2, -2, -2, -2, 0]
데미지 배열이 완성됩니다.
이를 이제 2차원 배열로 확장시켜보겠습니다. 데미지는 동일하기에 위로도 같은 데미지의 행이 있다고 가정해보겠습니다.
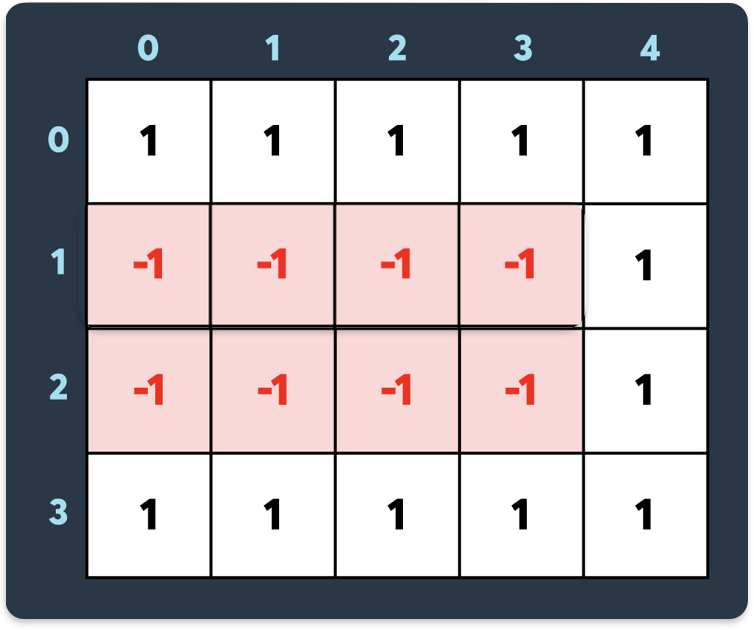
위 그림처럼 맵에 데미지를 준다고 가정한다면
[[0, 0, 0, 0, 0], [-2, -2, -2, -2, 0], [-2, -2, -2, -2, 0], [0, 0, 0, 0, 0]]
이렇게 됐을 때 누적합을 이용한 값은
[[0, 0, 0, 0, 0], [-2, 0, 0, 0, 2], [0, 0, 0, 0, 0], [2, 0, 0, 0, -2]] 로
우측으로 먼저 누적합 시킨뒤 아래로 누적합 시킨다면, (동시에 진행할 경우 다르게 계산됨.)
[[0, 0, 0, 0, 0], [-2, -2, -2, -2, 0], [-2, -2, -2, -2, 0], [0, 0, 0, 0, 0]]
이렇게 동작이 예상됩니다.
즉 skill 범위인 r1, c1, r2, c2 를 사각형을 그렸을때 주어진 두점은 degree, 나머지 꼭지점은 -degree 라 생각하시면 됩니다.
board[r1][c1], board[r2+1][c2+1] = degree
board[r1][c2+1], board[r2+1][c1] = -degree
문제 해결 코드
def solution(board, skill):
answer = 0
new_board = [[0] * (len(board[0])+1) for i in range(len(board)+1)]
for s_type, r1, c1, r2, c2, degree in skill:
if s_type == 1:
degree *= -1
new_board[r1][c1] += degree
new_board[r2+1][c2+1] += degree
new_board[r1][c2+1] -= degree
new_board[r2+1][c1] -= degree
for x in range(len(board)+1):
for y in range(1, len(board[0])+1):
# 가로 누적합
new_board[x][y] += new_board[x][y-1]
for x in range(len(board)):
for y in range(len(board[0])):
# 세로 누적합
if 0 < x:
new_board[x][y] += new_board[x-1][y]
if new_board[x][y] + board[x][y] > 0:
answer += 1
return answer정리
시간복잡도 계산하는 과정과 시간복잡도 해결을 위한 알고리즘을 떠올리는 과정이 어려웠고 구현 자체는 어렵지 않았지만 2차원 누적합이라는 처음보는 알고리즘으로 재밌게 풀었던 문제였습니다.
감사합니다. :)