Dynamic Programming
다이나믹 프로그래밍은 divide & conquer와 비슷한 전략을 이용한다. 하나의 문제를 여러 개의 subProblem으로 나눠서 계산을 하고자 한다. 차이점은 DP 테이블을 사용해서 subProblem을 해결하면 이 솔루션을 테이블에 저장해둔다. 즉, 중복된 계산을 하지 않는다.
Top-down approach(재귀)
점점 작은 문제에 대해 접근한다. 한번 저장한 것에 대해서 풀기 때문에 memorization 방법이라고도 한다.
Bottom-up approach(loop)
작은 문제에서 큰 문제로 접근한다. 예를 들어 i=2부터 n까지 sub[i] = sub[i-1] + sub[i-2]이다.
Matrix-Chain Multiplication
인풋으로 n개의 매트릭스이고 곱센연산을 최소로 만드는 순서를 만드는 알고리즘이다. 어떤 순서로 곱셈 연산을 해야 값이 최소가 되는지를 구하는 알고리즘이다.

- 1) 구조를 파악한다.
- 2) 점화식을 세운다.
- 3) 계산을 수행한다.
m[i,j] = min {m[i,k] + m[k+1,j] + Pi-1PkPj}
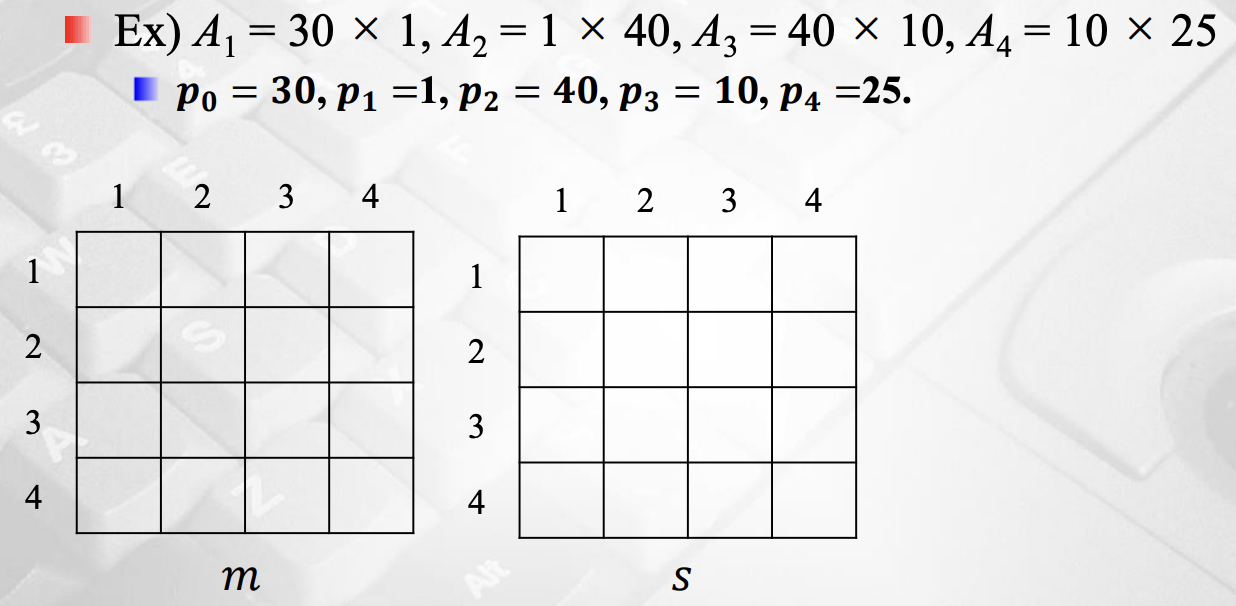
우선 대각선은 행렬이 하나만 있을 때의 곱셈이다. 하나만 있을 때는 0번이기 때문에 0으로 다 초기화 해준다. 매트릭스의 길이가 1인 것부터 점점 하나씩 늘려갈 것이다.

위와 같이 대각선을 기준으로 행렬이 한개, 두개, ... 이렇게 증가시킬 것이다.
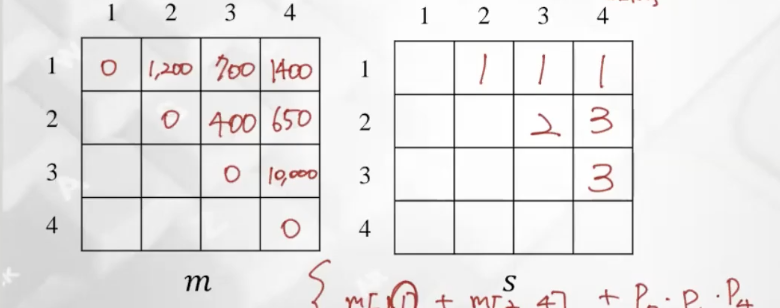
먼저 m[1,2] = (A1)(A2) 이렇게 하나만 가능한 경우이기 때문에 m[1,1] + m[2,2] + P0P1P2로 계산한다. = 0 + 0 + 1200 = 1200이다. S테이블에는 k값인 1을 넣어준다.
m[2,3] = (A2)(A3) 이렇게 하나만 가능하기 때문에 m[2,2] + m[3,3] + P1P2P3 = 400이 된다. S테이블에는 k값인 2를 넣어준다.
m[3,4] = (A3)(A4) 이렇게 하나만 가능하기 때문에 m[3,3] + m[4,4] + P2P3P4 = 10000이 된다. S테이블에는 k값인 3을 넣어준다.
m[1,3] = (A1)(A2A3) 또는 (A1A2)(A3)이 있다. = m[1,1] + m[2,3] + P0P1P3 = 0 + 400 + 300 = 700 또는 m[1,2] + m[3,3] + P0P2P3 = 1200 + 0 + 12000 = 13200 따라서 700을 넣어주고 s테이블에는 k값인 1을 넣어준다.
m[2,4] = (A2)(A3A4) 또는 (A2A3)(A4)이 있다. = m[2,2] + m[3,4] + P0P1P3 = 0 + 10000 + 1000 = 11000 또는 m[2,3] + m[4,4] + P0P2P3 = 400 + 0 + 250 = 650 따라서 650을 넣어주고 s테이블에는 k값인 3을 넣어준다.
m[1,4] = (A1)(A2A3A4) 또는 (A1A2)(A3A4) 또는 (A1A2A3)(A4)가 있다. = m[1,1] + m[2,4] + P0P1P4 = 0 + 650 + 750 = 1400 또는 m[1,2] + m[3,4] + P0P2P4 = 1200 + 10000 + 30000 = 41200 또는 [1,3] + m[4,4] + P0P3P4 = 700 + 0 + 7500 = 8200, 따라서 1400을 넣어주고 s테이블에는 k값인 1을 넣어준다.
수행 시간은 O(n^3) time 이고, 공간은 O(n^2) space 이다.
M테이블 수도코드

S테이블 수도코드

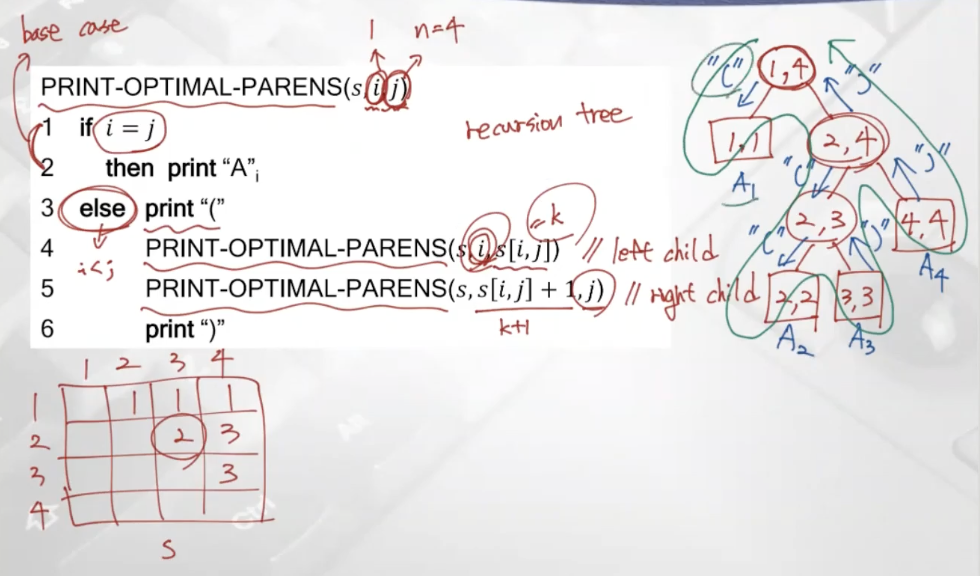
위 그림을 살펴보면 i는 1이고 j는 4이다. 그렇다면 루트는 (1,4)이다. 위 S테이블에서 (1,4)는 1이므로 k가 1이된다. 따라서 왼쪽 자식으로 (1,1) 오른쪽 자식으로(2,4)가 된다. 마찬가지로 (2,4)sms 3이므로 왼쪽 자식은 (2,3) 오른쪽 자식은 (4,4)가 된다. 왼쪽 자식으로 가기 전에 왼쪽 괄호를, 오른쪽 자식이 끝나면 오른쪽 괄호를 수행해준다.