Transitive Closure
그래프 G에 대해서 한 버텍스로부터 다른 버텍스까지 direct하게 갈 수 있는 엣지가 없다면 연결을 해준다. n번의 DFS 알고리즘을 수행한다면 G의 Transitive Closure을 알 수 있다.
이 알고리즘의 수행시간은 O(n(n+m)) time이다. m이 n^2에 수렴하면 O(n^3) time에 수행 가능하다.
인접행렬로 구하면 O(n^3) time에 수행 가능하다.
Floyd-Warshall Transitive Closure
phase K를 수행한다면 1부터 K-1까지의 정보를 가지고 수행한다. 예를 들어 i부터 K까지 가는 길이 있고 K에서 j까지 가는 길이 있는데 받은 정보에서 i에서부터 j까지 가는 길이 없다면 하나의 엣지를 더 추가해주는 것이다.

인풋은 다이그래프 G이고, 아웃풋은 Transitive Closure인 G*.이다. i는 1부터 모든 버텍스에 대해서 넘버링을 해준다. G0은 그래프 G를 카피한 것이다. G2는 버텍스2번까지 처리한 결과를 나타내고, Gk는 k버텍스까지 처리한 결과를 의미한다. i에서 k까지 가는 간선이 있고 k에서 j까지 가는 간선이 있는데 i부터 j까지 가는 간선이 없다면 그 간선을 추가한다.
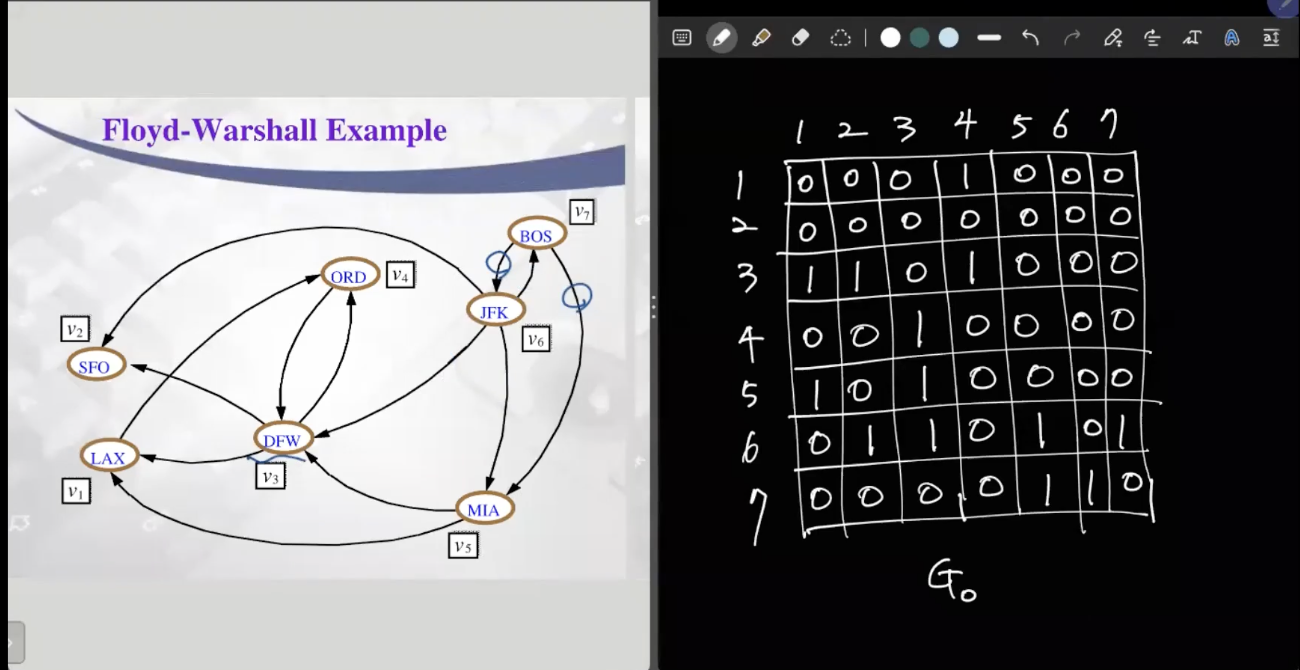
위 그래프는 G0의 그래프이다. 초기 그래프에서 각 버텍스마다 갈 수 있는 버텍스에는 1을 적어주고 없으면 0을 적어준다.
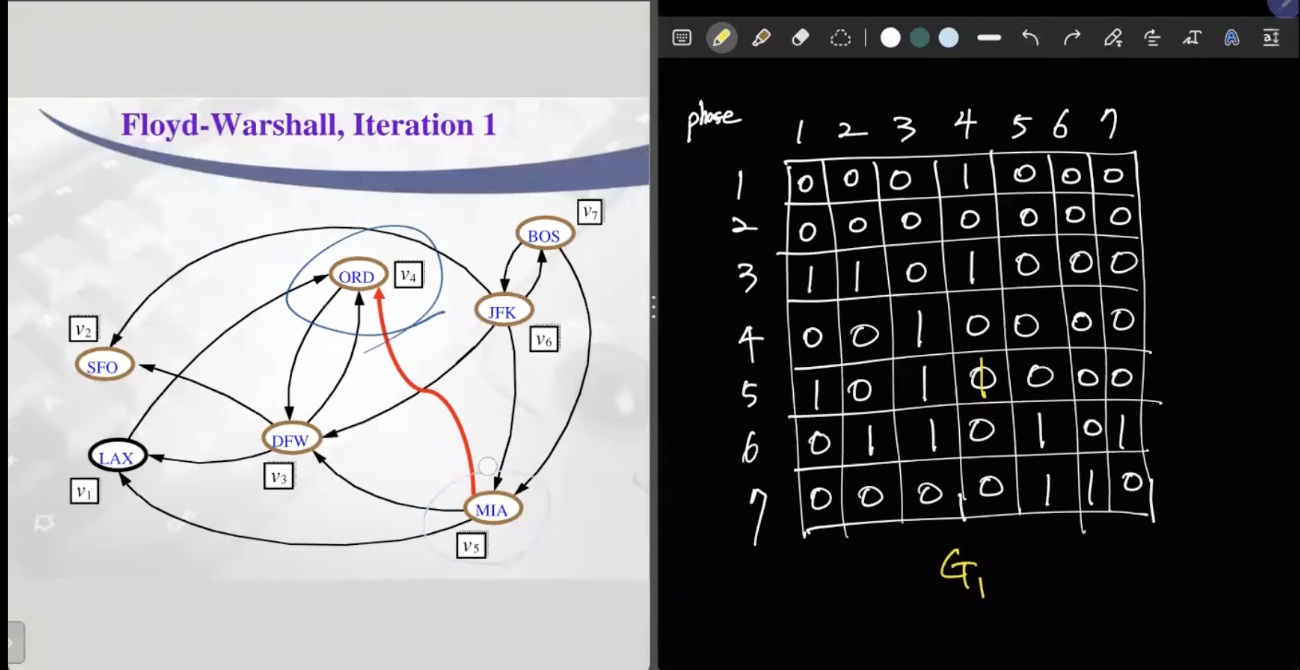
여기서부터 집중이 필요하다. 우선 1번 버텍스에 대해서 살펴볼 것이다. 1번에서부터 아래로 쭉 내린다. 3번으로 가는 버텍스가 있다. 그러면 1번 행을 우측으로 쭉 살펴보면서 거쳐가는 버텍스가 있다면 아래로 내려본다. 여기서는 4번이 그에 해당한다.(4,3)에 이미 1이 적혀있으므로 패스한다. 그러면 또 위에서부터 아래로 쭉 스캔한다. 5번이 1로 되어있다. 다시 우측으로 쭉 살펴보면서 아까 확인했던 4번에 대해서 (4,5)를 확인한다. 0이므로 1로 바꿔준다. 이런식의 작업을 반복한다.
All-Pairs Shortest Paths
이 문제는 Floyd-Warshall을 n번 호출해서 해결할 수 있다.

위 그림이 초기화한 그래프 G0이다. 나에서 나로 가는 버텍스는 모두 0으로 초기화하고, 버텍스에서 버텍스로 가는데 weight가 있으면 저장해주고 아니면 무한대로 초기화 해준다.

위 그림이 D1이다. Floyd-Warshall 방법과 마찬가지로 먼저 A에 대한 열을 쭉 스캔한다. B에서 2를 만났으므로 A를 오른쪽으로 쭉 스캔한다. 2를 만난 것은 B이기 때문에 같은 곳으로는 연결될 수 없어 스킵한다. F에서 9를 만난다. 그렇다면 B와 F가 만나는 지점에 그 둘을 더한 값을 넣어준다. 또 G와 만나는데 B와 G를 더한 값은 7이고 기존에 6이 적혀있으므로 그냥 스킵한다. 이것을 반복해주면 된다.
위 수행시간은 O(n^3) time이다.