[CS] 알고리즘 Graphs and Graph Traversals

Directed Graph(digraph)

digraph는 vertex V와 edge인 E의 집합으로 정의할 수 있다. 여기서 E는 두개의 vertex 쌍으로 정의한 집합이다(v.w). 이 쌍은 순서가 있는 쌍으로 정의된다. 순서가 있기 때문에 (v,w)와 (w,v)는 완전히 다르다.
v를 source, origin, start라고 부르기도 하고, w를 destination 또는 end라고 부른다. 아니면 화살표의 모양을 보고 v를 tail, w를 head라고 하기도 한다. self-loop를 정의할 수 있다(v,v).

Undirected Graph(graph)

undigraph는 vertex V와 edge인 E의 집합으로 정의할 수 있다. 여기서 E는 두개의 vertex 쌍으로 정의한 집합이다(v.w). 이 쌍은 순서가 없는 쌍으로 정의된다. {v,w}는 두개가 서로 달라야 한다. 반면 undigraph에서는 self-loop를 정의할 수 없다. 정의만 잘 해준다면 {}대신 ()를 사용하기도 한다.

incident(인접하다)

엣지와 버텍스간의 관계를 설명할 때 쓰는 용어이다.

adjacent(인접하다)

버텍스와 버텍스간의 관계를 설명할 때 쓰는 용어이다.

Weighted Graph

엣지마다 정보를 가지고 있다.

그래프 표현법

보통 그래프 G = (V,E)로 주어진다. n = |V|, m = |E|이다. 여기서 보통 input Size를 n+m이라고 한다. 따라서 O(n+m) time 알고리즘은 linear Time에 수행되는 알고리즘이다.

그래프 a를 가지고 (b)는 인접 행렬로 표현한 것이고, (c)는 인접 리스트로 표현한 것이다.

(b)는 버텍스의 개수 n x n으로 되어있다. 그리고 버텍스 사이에 엣지가 존재하면 1을, 없으면 0을 넣어주면 된다. 그리고 방향성이 없기 때문에 대각선을 기준으로 양쪽이 대칭적인 값을 가진다. 자기 자신으로 가는 엣지는 없기 때문에 0을 넣는다. n x n이기 때문에 O(n^2) space를 차지하게 된다.

(c)는 각각의 버텍스에 관해서 인접해 있는 것을 리스트로 넣어주면 된다. nil은 다음 원소가 없다는 것을 의미한다. 엣지의 개수는 모두 2m개이기 때문에 O(m) = O(n+m) space를 차지하게 된다.

수행시간

1) v.incidentEdges() :

• adjancy matrix: O(n) time -> 행을 살펴봐야 하기 때문에 n개를 살펴봐야 한다.
• adjancy list: O(deg(v)) time -> 해당 리스트를 살펴보면 된다.

2) v.adjacentTo(w) :

• adjancy matrix: O(1) time -> 해당 인덱스에 바로 접근이 가능하다.
• adjancy list: O(min(deg(v), deg(w)) time -> undigraph일 때에만 가능하다.
  : O(deg(v)) time -> digraph일 때 가능하다.
  

그래프 관련 용어

Subgraph

G = (V,E) 이고 G' = (V',E')는 V'<=V, E'<=E일 때 Subgraph이다.

Complete graph

완전그래프는 모든 정점 사이에 엣지가 존재하는 것을 의미한다. Undigraph에서는 각 버텍스는 자기 자신을 제외하고 모두 연결이 되어있어야만 한다. n-1개 + n-2개 + n-3개+ ... +1개의 엣지(n(n-1)/2)를 가진다. digraph에서는 각각 2개씩 가지므로 n(n-1)개의 엣지를 가진다.

Path, simple path, reachable

여기에서 Path는 연결된 엣지들의 나열로 정의할 수 있다. path P = <v0v1, v1v2, ...vk-1vk>. Path의 길이는 오른쪽 끝에 있는 값, v1,v2,...vk k가 길이이다. 버텍스의 나열로 정의했다면 path의 길이는 버텍스의 길이 - 1이다. Undigraph에서 path는 한쪽 방향으로만 연결이 되어야만 한다. 중간에 반대로 가거나 방향을 바꿀 수는 없다. Simple path는 path 상에서 버텍스가 모두 다르면 simple path라고 한다. reachable은 버텍스와 버텍스간의 관계를 의미한다. 한 버텍스로부터 다른 버텍스까지 갈 수 있는 path가 있으면 reachable하다고 한다.

Connected, Strongly Connected

Connected는 undigraph에서 사용하는 용어이다. 그래프에서 모든 버텍스가 엣지로 연결이 되어 있다면 이 그래프는 connected 되었다고 한다. 모든 버텍스가 하나의 엣지로 다 연결되었다는 것을 의미하는 것이 아니다. 임의로 버텍스를 선택했을 때 엣지가 연결만 되어있으면 된다.
Strongly Connected는 digraph에서 사용하는 용어이다. 임의의 두 정점이 reachable하다면 Strongly Connected 되어있다고 한다. 임의의 두 정점을 선택했을 때, 서로 갈 수 있는 path가 있을 때를 의미한다.

Cycle, simple cycle

Cycle은 시작 정점과 끝 정점이 같은 Not Empty path를 의미한다. 여기서 Not Empty path은 path의 길이가 0인 것을 말한다. digraph에서는 self-loop가 되기 때문에 최소 길이가 1이면 된다. 하지만 undigraph에서는 self-loop가 되지 않기 때문에 최소 길이가 3이다.
simple cycle은 시작 정점과 끝 정점을 제외하고 버텍스가 다른 사이클을 의미한다.

acyclic

사이클이 없는 그래프를 의미한다.

undirected forest

하나 이상의 트리를 forest라고 한다. acyclic 해야하고, undirected graph를 만족하면 된다.

free tree, undirected tree

free tree는 undirected tree와 같은 의미이다. 첫째로 connected 해야하고, acyclic해야 한다. 마지막으로 undirected graph를 만족해야 한다.

rooted tree

root를 가진 free tree를 의미한다.

Connected component

undigraph에 대한 용어이다. digraph에서는 앞에 strongly를 붙여주면 된다. Connected component는 최대로 연결된 subgraph를 의미한다.

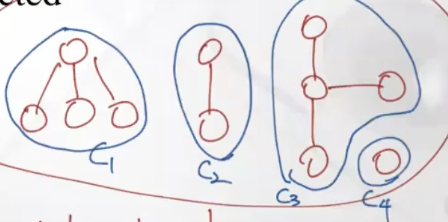
위에 그래프에서는 4개의 Connected component가 있는 것이다.

위 그림에서 strongly connected component에서는 3개가 존재하는 것이다.

degree

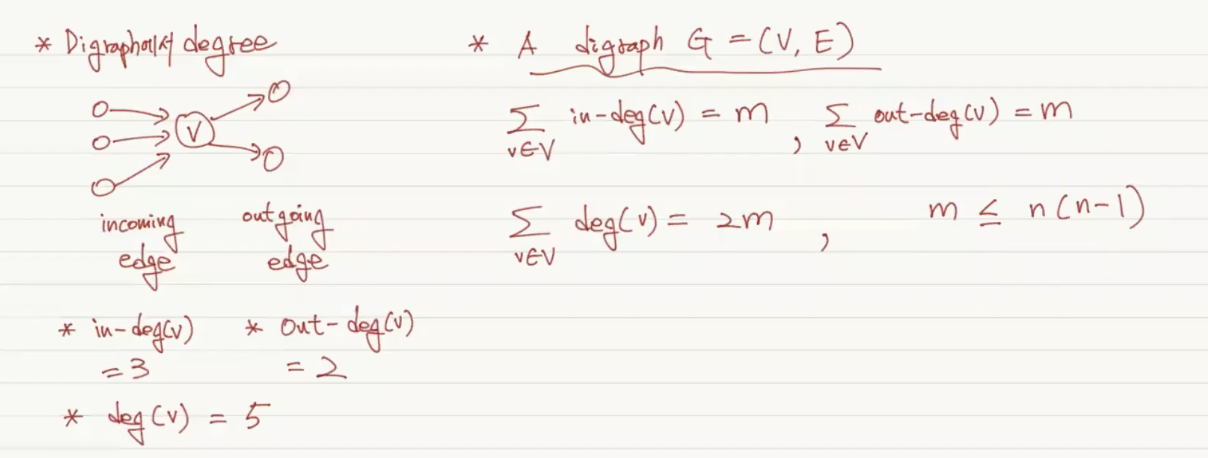
digraph는 incoming edge가 있고 outgoing edge가 있다. 이 두개를 합한 것이 degree이다. digraph에서는 in-degree의 수와 out-degree의 수는 같다. m은 모든 엣지의 수(n(n-1))보다 작거나 같아야만 한다.

undigraph에서는 in, out개념이 없다. 총 합 m은 모든 엣지의 수 (n(n-1)/2)보다 작거나 같아야 한다.

• undigraph에서는 만약 G가 connected라면 m >= n-1이다.
• undigraph에서는 만약 G가 tree라면 m = n-1(버텍스보다 하나 작다) // acyclic, undirected
• undigraph에서는 만약 G가 forest라면 m <= n-1이다. // acyclic, undirected

Traversal Graph

• Vertex의 상태 : undiscovered, discovered, finished
• Edge의 상태 : unexplored, explored

BFS(너비 우선 탐색)

영역을 넓혀가는 전략을 이용한다. 우선 탐색을 진행할 시작 버텍스를 정한다. 그리고 그 정점의 distance를 0으로 해놓는다. 같은 distance를 가진 영역을 우선적으로 다 탐색한다. 더이상 discovered 할 수 없는 버텍스까지 가는 것이다.

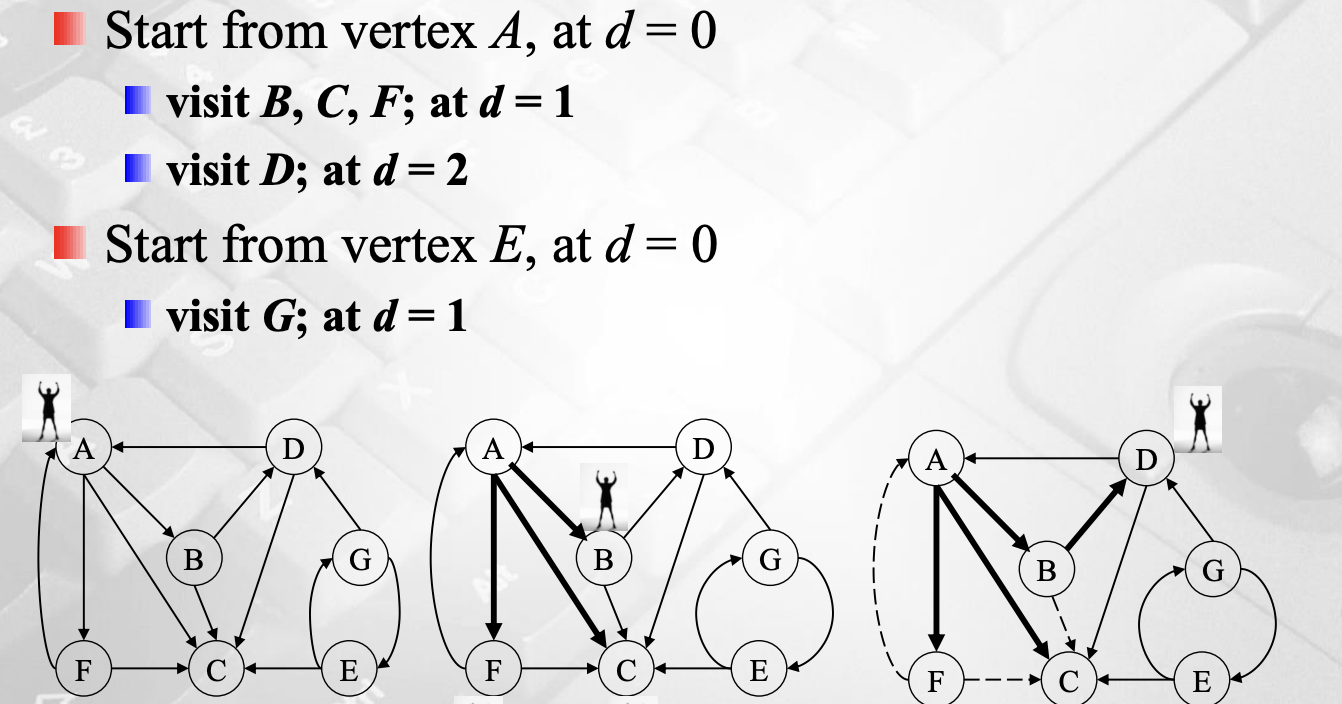
BFS에서는 큐를 사용하는 것을 전제로 한다. 큐가 비어있다면 큐에 집어 넣는다. 그리고 distance로 분류를 해준다. 만약 discovered로 바뀐다면 enqueue해주고, A에서 갈 수 있는 노드를 사전 순서대로 큐에 집어넣는다. 마찬가지로 discovered를 해주면 enqueue해주고 또 B에서 갈 수 있는 노드를 사전 순서대로 큐에 집어 넣는다. 이것을 반복한다. E와 G는 새로운 큐를 만들어주고 distance를 0으로 초기화 해준다.

BFS 알고리즘을 이용하면 시작 버텍스부터 원하는 노드까지의 최단 거리를 구할 수 있다. 하지만 엣지의 weighted가 주어진다면 최단거리를 구할 수 없다. 최단 경로를 구하기 위해서는 추가적으로 parent라는 정보가 필요한데 큐에서 확인해보면 A는 없으니까 -1을, B C F의 parent는 A이다. 이러한 정보를 저장하고 새로운 큐를 만들면 D를 push, D의 parent인 B를 push, B의 parent인 A를 푸시... 이렇게 해서 -1을 만날 때까지 해주면 된다. 그 결과가 최단 경로이다.

DFS(깊이 우선 탐색)

갈 때까지 가보자는 전략을 이용한다. 우선 탐색을 진행할 시작 버텍스를 정한다. 그리고 그 정점의 distance를 0으로 해놓는다. 인접한 버텍스를 +1해서 갈 때까지 가는 전략이다. 더이상 discovered 할 수 없는 버텍스까지 가는 것이다. finished가 되면 또 이전 버텍스로 가서 또 갈 때까지 가는 것이다.

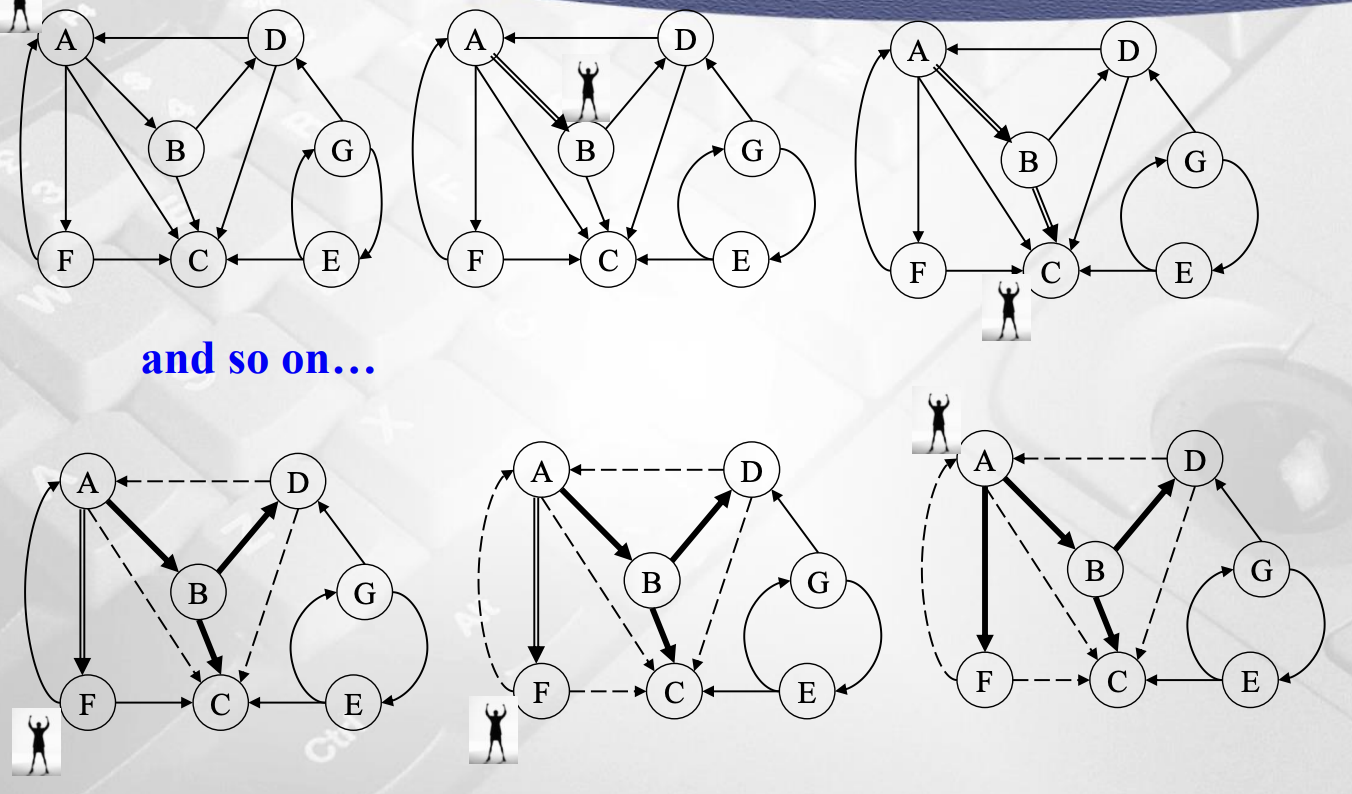
일단 visit할 수 있는 버텍스가 여러 개 있을 경우 사전순으로 작은 것부터 visit한다고 가정을 하고 시작한다. 처음에 모든 버텍스에 대해서 undiscovered로 초기화를 해주고, 모든 엣지들에 대해서는 unexplored로 초기화 해줘야 한다. A는 discovered로 상태를 변경해주고 d=0으로 해준다. 갈 수 있는 아웃풋이 여러 개인 경우 사전순으로 갈 수 있으므로 B, 그리고 C로 간다. B와 C는 discovered로 바꿔준다. C일 때 d=2이고 C에서 갈 수 있는 output이 없으므로 finished하고 뒤칸인 B로 돌아간다. 그리고 D를 discovered로 바꿔주고 visit 해준다 d=2가 된다. D에서도 갈 수 있는 노드가 없으므로 finished해주고 B로 간다. 이 과정을 반복해주면 된다. F까지 간다면 더이상 A에서 갈 수 있는 곳이 없게 된다. 그때는 사전순으로 더 작은 E를 d=0으로 초기화해주고 G의 distance=1, finished하고 E도 finished 해준다.

위 DFS를 바탕으로 visited 순서와 finished 순서를 출력할 수 있다. 전자는 "A B C D F E G" 후자는 "C D B F A G E"이다.

엣지의 종류는 tree edge, back edge, descendant edge, cross edge가 있다. undicovered enge에서 dicovered enge가 되면 tree edge로 바꿔준다. 그리고 이미 discovered가 되어 있는데 그 노드가 조상이라면 back edge, 후손이라면 descendeant edge로 바꿔준다. 그 외의 경우는 cross edge이다.

Strongly Connected Component

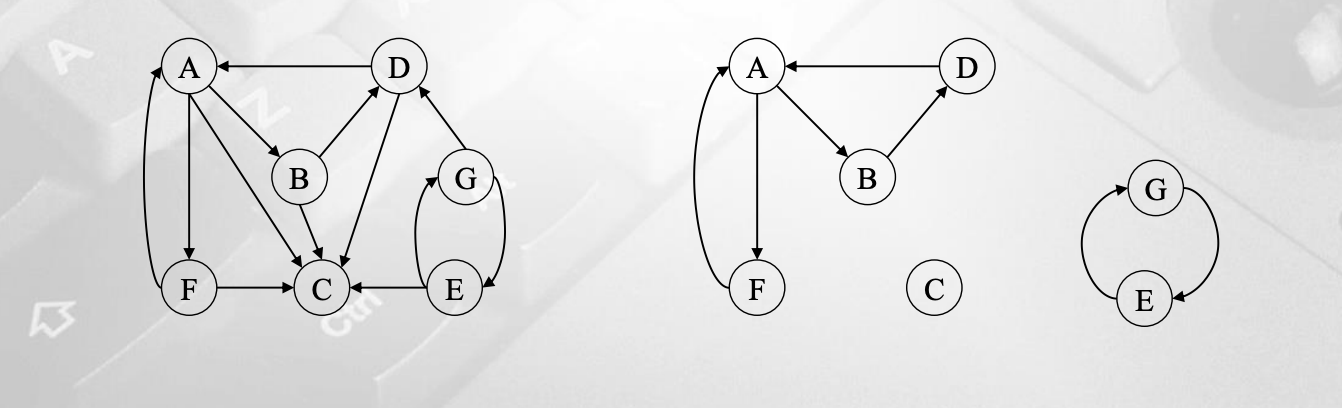
입력으로 digraph가 주어진다. 그래프에 있는 버텍스가 reachable 하다면 Strongly Connected 하다고 한다. 이 SCC를 해결할 수 있는 알고리즘은 2번의 DFS를 수행하면 해결할 수 있다.
크게 두단계로 나뉘는데 우선 첫번째 DFS를 수행할 때에는 finished가 된 상태에는 바로 스택에 push 할 것이다. 한마디로 finished되는 순서대로 스택에 저장되어 있다.
두번째 단계는 G의 방향만 반대로 바꾸는 Gt를 생성해준다. 하지만 이 수행 순서는 스택에서 pop되는 순서이다.

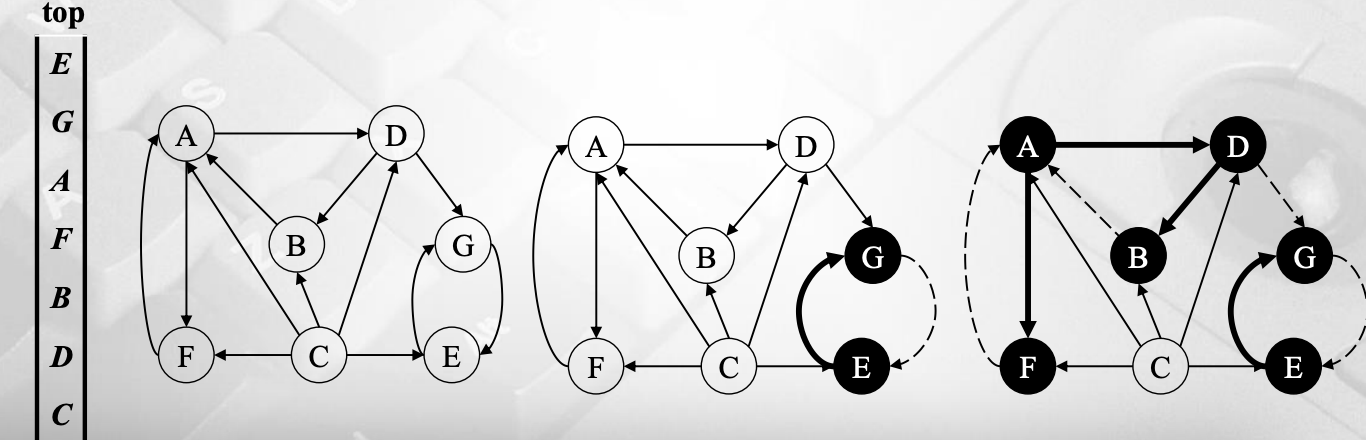
위 그래프를 예시로 살펴보면 C D B F A G E 순서대로 finished가 된다.

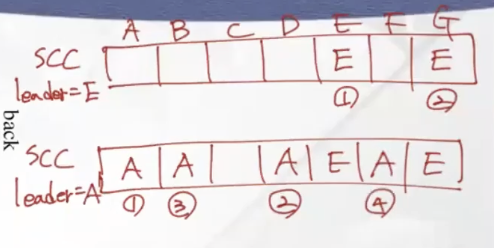
위와 같이 n개를 담을 수 있는 배열을 하나 더 만들어준다. 스타트 하는 리더를 정해주고 해당 노드에서 discovered가 된다면 그 자리에 해당 리더를 적어준다. finished할 때까지 적어주는 것이다. 저렇게 해서 SCC를 구할 수 있다.

1단계는 상수시간에 수행 O(n+m) time에 가능하다. 2단계도 상수시간에 수행 O(n+m)이 가능하다. 총 수행시간은 O(n+m) time이다.